人教版高中物理选修3-3第八章第三节理想气体状态方程应用(共14张PPT)
文档属性
| 名称 | 人教版高中物理选修3-3第八章第三节理想气体状态方程应用(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-05 22:27:05 | ||
图片预览




文档简介
(共14张PPT)
理想气体状态方程应用
人教版选修3-3 物理
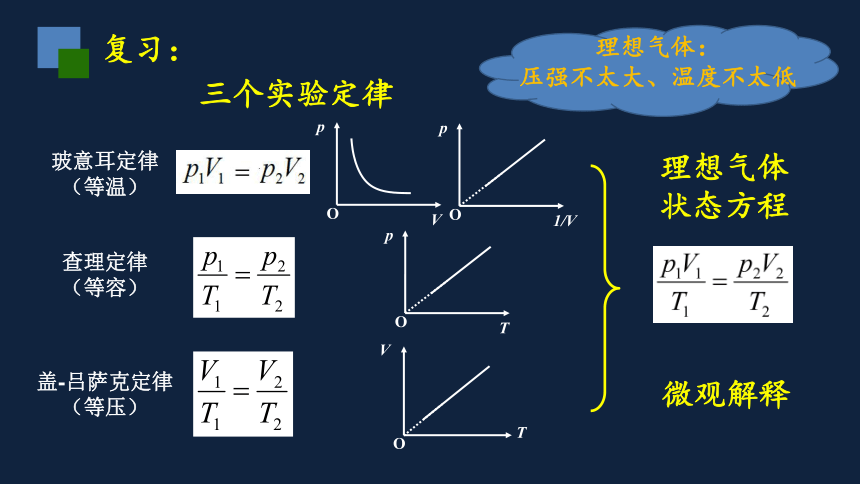
复习:
理想气体状态方程
三个实验定律
O
p
1/V
O
p
V
玻意耳定律
(等温)
O
p
T
查理定律
(等容)
O
V
T
盖-吕萨克定律
(等压)
理想气体:
压强不太大、温度不太低
微观解释
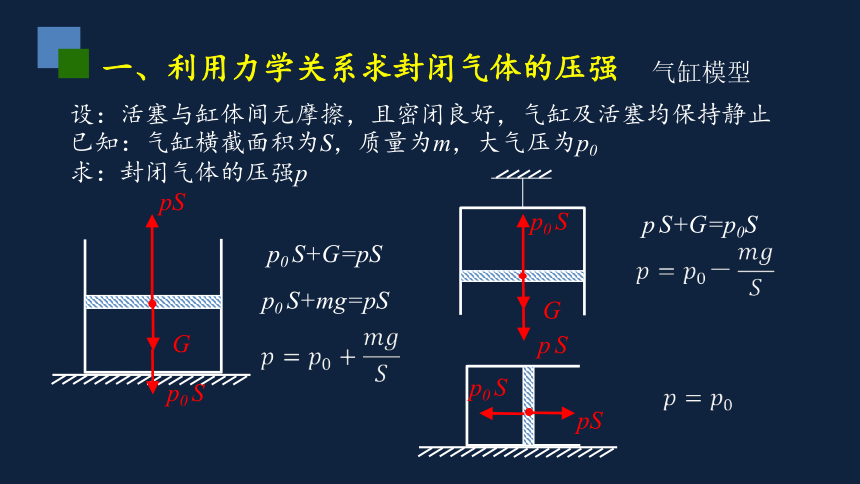
一、利用力学关系求封闭气体的压强
气缸模型
已知:气缸横截面积为S,质量为m,大气压为p0
求:封闭气体的压强p
G
p0 S
pS
p0 S+G=pS
p0 S+mg=pS
G
p S
p0 S
p S+G=p0S
p0 S
pS
设:活塞与缸体间无摩擦,且密闭良好,气缸及活塞均保持静止
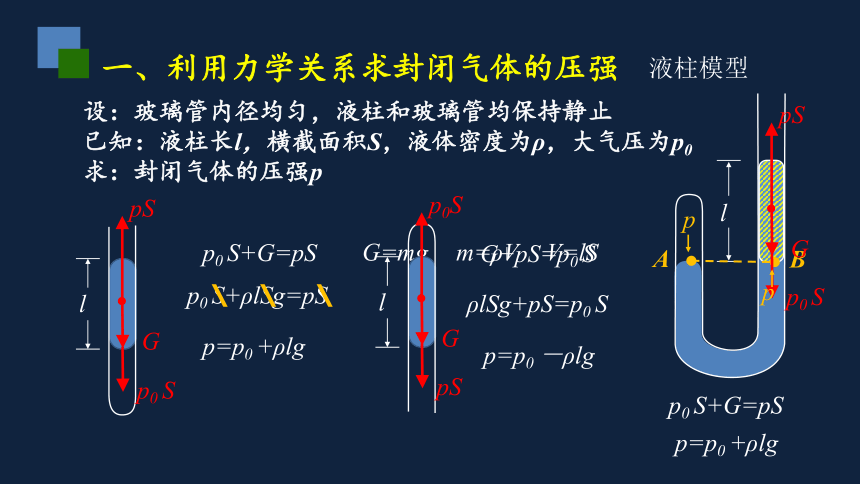
一、利用力学关系求封闭气体的压强
液柱模型
l
设:玻璃管内径均匀,液柱和玻璃管均保持静止
已知:液柱长l,横截面积S,液体密度为ρ,大气压为p0
求:封闭气体的压强p
G
p0 S
pS
p0 S+G=pS
p0 S+ρlSg=pS
G=mg
m=ρV
V=lS
p=p0 +ρlg
\ \ \
l
G
pS
p0S
G+pS=p0 S
p=p0 -ρlg
ρlSg+pS=p0 S
l
A
B
G
p0 S
pS
p
p
p0 S+G=pS
p=p0 +ρlg
二、实例应用
长为 100cm、内径均匀的细玻璃管,一端封闭、一端开口,当开口竖直向上时,用 20cm水银柱封住 L1=49 cm长的空气柱,如图所示.当开口竖直向下时(设当时大气压强为 76 cmHg,即1×105 Pa),管内被封闭的空气柱长为多少?
:
设末状态时(管口向下)无水银溢出,
根据玻意耳定律:p1V1=p2V2
解得 L2=84 cm
84 cm+20 cm>100 cm
所以,假设错误,会有水银溢出
设末状态管内水银柱长 x cm
则 p2=(76-x) cmHg,
V2=(100-x)S
根据玻意耳定律 p1V1=p2V2
x2+176x+2896=0
解得 x=18.4,x′=157.6(舍去)
空气柱长度 =81.6 cm.
单位只要左右对称
二、实例应用
如图所示,两端封闭粗细均匀、竖直放置的玻璃管内有一段长为h的水银柱,将管内气体分为两部分.已知l2=2l1,若使两部分气体同时升高相同的温度,管内水银柱将(设原来温度相同) ( )
A.不动 B.向上运动 C.向下运动 D.无法确定
思路:假设管内水银柱相对玻璃管不动
Δp1 ? Δp2
根据查理定律对于上段气柱有
同理对于下段气柱
由水银柱初始平衡 p1=p2+ρgh >p2
Δp1>Δp2, 水银柱向上移动
B
G
p2S
p1S
O
p
T
A(T, p)
T
O
V
T
A(V, p)
T
等容变化
等压变化
假设管内水银柱相对玻璃管不动的前提下,对比两段空气柱的p-T图线
思考:如果玻璃管始终是水平放置的,结果又应该如何?
答案:不会移动
二、实例应用
一容器中装有某种气体,且容器上有一小孔跟外界大气相通,原来容器内气体的温度为27℃,如果把它加热到127℃,从容器中逸出的气体质量是原来质量的多少倍?
问题:容器中的气体显然不满足“一定质量的气体”这个条件
研究对象:没逸出和逸出的气体的总和
初态:T1=(273+27)K=300 K,V1;
末态:T2=(273+127)K=400 K,V2 = V1 +ΔV.
由盖—吕萨克定律
得
思路:等压变化
二、实例应用
一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示,若状态D的压强是2×104 Pa.
请在甲、乙图中分别画出该状态变化过程的p-T图象,以及p-V图象
二、实例应用
一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示,若状态D的压强是2×104 Pa.
请在甲、乙图中分别画出该状态变化过程的p-T图象,以及p-V图象
A B C D
p /×104Pa
V/m3 1 1 4 4
T /×102K 2 8 8 4
思路:理想气体状态方程
4
16
4
2
二、实例应用
A B C D
p /×104Pa 2
V/m3 1 1 4 4
T /×102K 2 8 8 4
4
16
4
A
B
C
D
A
B
C
D
思路:
温度T相同时,则有
一定质量的气体经历如图所示的一系列过程,ab、bc、cd和da这四个过程在p-T图上都是直线段,其中ab的延长线通过坐标原点O,bc垂直于ab,而cd平行于ab,由图可以判断( )
A.ab过程中气体体积不断减小
B.bc过程中气体体积不断减小
C.cd过程中气体体积不断增大
D.da过程中气体体积不断增大
二、实例应用
①
②
③
=
BCD
再见!
理想气体状态方程应用
人教版选修3-3 物理
复习:
理想气体状态方程
三个实验定律
O
p
1/V
O
p
V
玻意耳定律
(等温)
O
p
T
查理定律
(等容)
O
V
T
盖-吕萨克定律
(等压)
理想气体:
压强不太大、温度不太低
微观解释
一、利用力学关系求封闭气体的压强
气缸模型
已知:气缸横截面积为S,质量为m,大气压为p0
求:封闭气体的压强p
G
p0 S
pS
p0 S+G=pS
p0 S+mg=pS
G
p S
p0 S
p S+G=p0S
p0 S
pS
设:活塞与缸体间无摩擦,且密闭良好,气缸及活塞均保持静止
一、利用力学关系求封闭气体的压强
液柱模型
l
设:玻璃管内径均匀,液柱和玻璃管均保持静止
已知:液柱长l,横截面积S,液体密度为ρ,大气压为p0
求:封闭气体的压强p
G
p0 S
pS
p0 S+G=pS
p0 S+ρlSg=pS
G=mg
m=ρV
V=lS
p=p0 +ρlg
\ \ \
l
G
pS
p0S
G+pS=p0 S
p=p0 -ρlg
ρlSg+pS=p0 S
l
A
B
G
p0 S
pS
p
p
p0 S+G=pS
p=p0 +ρlg
二、实例应用
长为 100cm、内径均匀的细玻璃管,一端封闭、一端开口,当开口竖直向上时,用 20cm水银柱封住 L1=49 cm长的空气柱,如图所示.当开口竖直向下时(设当时大气压强为 76 cmHg,即1×105 Pa),管内被封闭的空气柱长为多少?
:
设末状态时(管口向下)无水银溢出,
根据玻意耳定律:p1V1=p2V2
解得 L2=84 cm
84 cm+20 cm>100 cm
所以,假设错误,会有水银溢出
设末状态管内水银柱长 x cm
则 p2=(76-x) cmHg,
V2=(100-x)S
根据玻意耳定律 p1V1=p2V2
x2+176x+2896=0
解得 x=18.4,x′=157.6(舍去)
空气柱长度 =81.6 cm.
单位只要左右对称
二、实例应用
如图所示,两端封闭粗细均匀、竖直放置的玻璃管内有一段长为h的水银柱,将管内气体分为两部分.已知l2=2l1,若使两部分气体同时升高相同的温度,管内水银柱将(设原来温度相同) ( )
A.不动 B.向上运动 C.向下运动 D.无法确定
思路:假设管内水银柱相对玻璃管不动
Δp1 ? Δp2
根据查理定律对于上段气柱有
同理对于下段气柱
由水银柱初始平衡 p1=p2+ρgh >p2
Δp1>Δp2, 水银柱向上移动
B
G
p2S
p1S
O
p
T
A(T, p)
T
O
V
T
A(V, p)
T
等容变化
等压变化
假设管内水银柱相对玻璃管不动的前提下,对比两段空气柱的p-T图线
思考:如果玻璃管始终是水平放置的,结果又应该如何?
答案:不会移动
二、实例应用
一容器中装有某种气体,且容器上有一小孔跟外界大气相通,原来容器内气体的温度为27℃,如果把它加热到127℃,从容器中逸出的气体质量是原来质量的多少倍?
问题:容器中的气体显然不满足“一定质量的气体”这个条件
研究对象:没逸出和逸出的气体的总和
初态:T1=(273+27)K=300 K,V1;
末态:T2=(273+127)K=400 K,V2 = V1 +ΔV.
由盖—吕萨克定律
得
思路:等压变化
二、实例应用
一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示,若状态D的压强是2×104 Pa.
请在甲、乙图中分别画出该状态变化过程的p-T图象,以及p-V图象
二、实例应用
一定质量的理想气体由状态A变为状态D,其有关数据如图甲所示,若状态D的压强是2×104 Pa.
请在甲、乙图中分别画出该状态变化过程的p-T图象,以及p-V图象
A B C D
p /×104Pa
V/m3 1 1 4 4
T /×102K 2 8 8 4
思路:理想气体状态方程
4
16
4
2
二、实例应用
A B C D
p /×104Pa 2
V/m3 1 1 4 4
T /×102K 2 8 8 4
4
16
4
A
B
C
D
A
B
C
D
思路:
温度T相同时,则有
一定质量的气体经历如图所示的一系列过程,ab、bc、cd和da这四个过程在p-T图上都是直线段,其中ab的延长线通过坐标原点O,bc垂直于ab,而cd平行于ab,由图可以判断( )
A.ab过程中气体体积不断减小
B.bc过程中气体体积不断减小
C.cd过程中气体体积不断增大
D.da过程中气体体积不断增大
二、实例应用
①
②
③
=
BCD
再见!
