五年级下册数学教案-质数和合数-人教版

教学设计
教 材： 小学数学教材五年级下册
课 题: 质数和合数

【教材分析】
《质数和合数》选自人教版小学数学教材第十册第二单元，它是在学生认识了因数与倍数的意义，熟练掌握了2、3和5的倍数特征的基础上进行的，同时为后面学习分解质因数，以及求最大公约数，最小公倍数奠定了基础，因此它在这一个单元中起着承前启后的作用。教材编排上，是让学生根据对一些数的因数进行汇总、对比、分类，从而从因数个数的角度上揭示出质数和合数的概念。

【学情分析】
知识储备上，学生通过前一阶段的学习已经掌握了因数与倍数的意义，学会了2、3、5倍数特征，并且积累了一些探索数学规律的基本方法和策略。心理特征上，本节课的教学对象是五年级的学生，该阶段的学生已具备了一定的观察、分析、理解的能力，同时对于感兴趣的活动有积极参与的意识。

【设计思路】
本节课我利用白板的对象移动，聚光灯，即时书写，拉幕、等强大的功能以及利用电子白板自带的多媒体交互资源有效地处理教学重难点。紧密围绕课的重点、根据学生的环境和接受能力设计行之有效的任务和活动，设计了“情境导入，激发兴趣——体验探究，揭示概念——应用概念，巩固拓展——分层练习，概念升华——课堂总结，课后延伸”五大环节。情境导入环节通过由大家都熟知的东方明珠引出数学王冠上的明珠——哥德巴赫猜想，激发起学生的探究数学问题的欲望，提高学生的学习兴趣。体验探究环节中设计了两个层次的探究活动，一是具体图形的探究，利用小正方形拼摆长方形的情境，初步感受数与因数个数的隐形联系，二是抽象数字的探究，研究20以内数的因数以及因数个数，从而揭示概念。应用概念环节利用课前发放的学号牌在全班进行互动，通过说一说、辨一辨等活动培养学生有条理地、清晰地阐述数学观点的能力，同时起到巩固新知的作用，随后再由学号牌上50以内的数字拓展到制作100以内的质数表，“20-50-100”的梯度设置体现了教学由易到难，由浅入深的理念，使课堂教学层层递进，环环紧扣。分层练习环节我设置了三种不同类型不同层次的题目，基础题进一步巩固判断质数合数的方法，拓展题体现数学与生活的密切联系，开放题培养学生思维发散的能力，同时渗透学生对数学文化的了解，提高学生探索数学问题的兴趣。

【教学目标】
1、知识技能
掌握质数和合数的概念，能正确判断一个数是质数还是合数。
2、数学思考
通过观察、思考、探究等过程，经历具体到抽象的认识和辨别过程，培养学生观察、比较、归纳、概括的能力，发展合情推理能力和初步的演绎推理能力、能有条理地、清晰地阐述判断一个数是质数还是合数的理由。
3、问题解决
学会将自己的想法和建议分享给他人，并能从他人的交流中形成评价和反思的意识，同时应用于自己的解决问题中。
4、情感态度
培养学生敢于探索科学之谜的精神，激发学生学习数学的兴趣。

【教学重、难点】
重点：理解质数和合数的意义
难点：掌握正确判断一个数是质数还是合数的方法

【教法、学法】
传统的教学中，往往是直接让学生通过对一些数的因数进行汇总、分类、对比，从而揭示出质数和合数的概念，而基于绝大多数学生对概念并不了解，同时该活动的主动权还是掌握在教师的手上，没有充分发挥学生的主体性。因此，在教学设计中我将教材进行了适当的改编，通过第一个教学实践的安排，让学生通过用小正方形拼摆长方形的活动初步感受数与因数个数间的内在联系，引导学生从因数个数的角度出发，进行第二次有选择的实践活动，任意选择1-20的数字进行探究，从而给学生自主获取质数和合数本质的机会。最后在学生掌握了概念的基础上，利用学号巩固概念，总结出判断质数和合数的方法，激发学生进一步探索和研究的欲望。

【教学准备】smart电子白板课件，学号牌，作业纸

【教学过程】
教学 环节 教学内容 活动设计 设计意图 媒体使用及分析（交互式电子白板的使用功能）
情 境 导 入 ， 激 发 兴 趣 引出哥德巴赫猜想。 谈话：你们去过上海吗？ 出示东方明珠图片。介绍东方明珠：它就像一颗璀璨的明珠屹立在中国的东方。 在我们的数学中，也有一颗闪耀的明珠。 那就是哥德巴赫猜想。 4、导入：今天这节课就与哥德巴赫猜想有关。 课前的谈话给学生们创造出宽松的环境，可以放松心情进入课堂。同时通过由大家都熟知的东方明珠引出数学王冠上的明珠——哥德巴赫猜想，激发起学生的探究数学问题的欲望，提高学生的学习兴趣。 1、利用翻板工具展示东方明珠图片2、引出哥德巴赫猜想时我应用了电子白板的对象移动功能，将隐藏在课件外的文字拖动到屏幕中，激发兴趣。
课 件 截 图
教学 环节 教学内容 活动设计 设计意图 媒体使用及分析（交互式电子白板的使用功能）
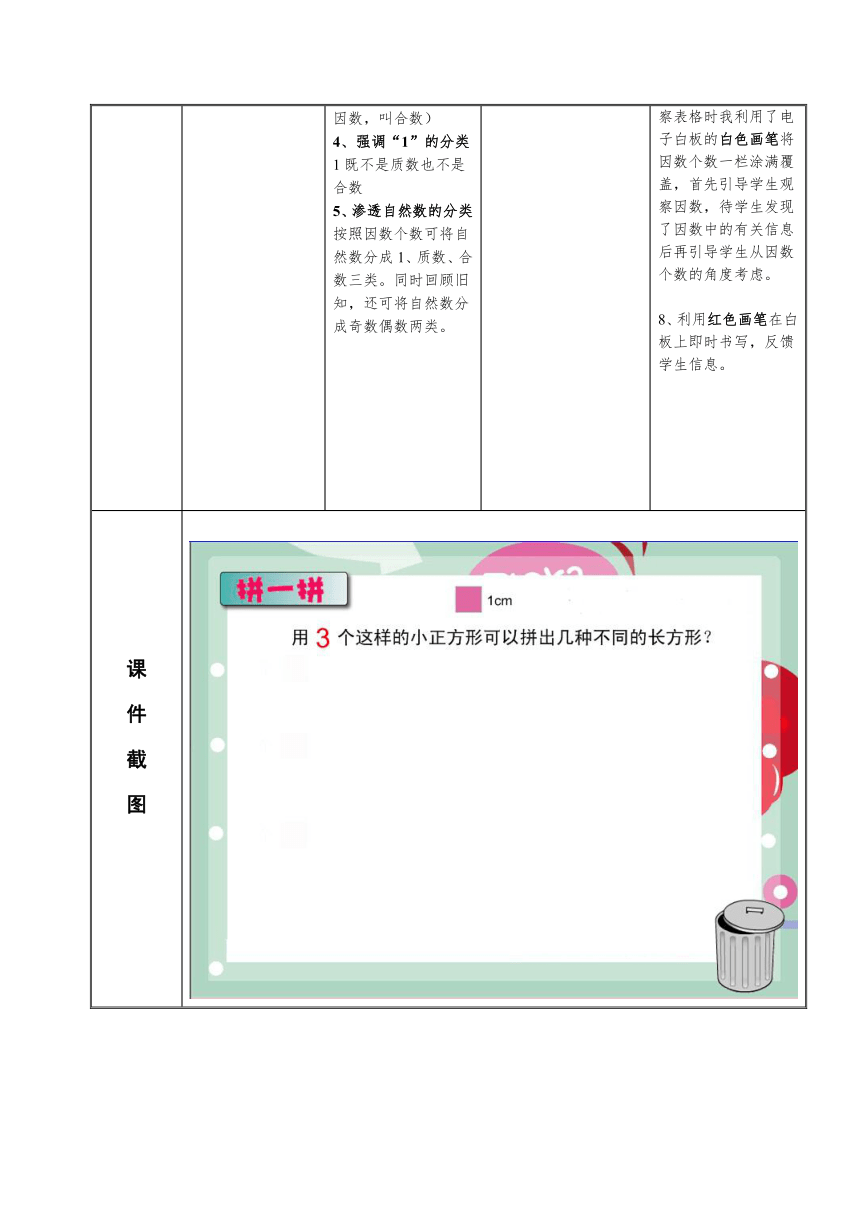
体 验 探 究 ， 揭 示 概 念 1、用小正方形拼摆长方形，感受数与因数个数间的隐性联系。 2、任意选择1-20的数字进行探究，发现一个数的因数以及因数个数的相关信息。 3、了解质数和合数的概念。 4、从因数个数的角度对自然数进行分类。 1、第一次探究 （具体图形）（1）用3个这样的能拼出几种不同的长方形？ （2）用4个呢？12个呢？ （3）如果继续增加正方形的个数，是不是长方形的种类就越多呢？ 思考问题：长方形的拼法与正方形的什么有关？ （A．个数的多少 B.个数的奇偶性 C.因数的个数）2、第二次探究 （抽象数字）自主探究：自由选择自己喜欢的数字（1-20），找出它的所有因数。师巡视。 指名学生到白板前完成表格。3、揭示质数和合数的概念这些数的因数有什么共同点？因数个数呢？①2、7、13（视课堂随机而定）为一类（揭示概念：只有1和它本身2个因数，叫质数）②6、7、12（视课堂随机而定）为一类（揭示概念：除了1和它本身以外，还有别的因数，叫合数）4、强调“1”的分类1既不是质数也不是合数5、渗透自然数的分类按照因数个数可将自然数分成1、质数、合数三类。同时回顾旧知，还可将自然数分成奇数偶数两类。 1、通过用小方块摆长方形或正方形初步感受数与因数个数间的隐性联系，适时地挖掘学生对概念的不同认识。通过小组交流、举例验证引导学生发现长方形的拼法与正方形个数的因数个数有关。为本节课揭示因数个数的有关问题奠定基础。 2、从因数个数的角度出发，进行第二次有选择的实践活动，任意选择1-20的数字进行探究，从而给学生自主获取质数和合数本质的机会。 3、学生到白板拖动数字，突破了ppt只能按照预设数字进行教学的局限性，课堂更加灵活多变，学生真正成为了课堂的小主人，体现了以学生为中心的教学理念。 4、根据学生完成的表格，进行观察、思考、对比、归纳等活动，培养学生搜集和处理信息的能力，给学生充分的自主学习空间，在与他人的交流中获取新知。 1、在第一次探究的活动中，我应用了电子白板的无限克隆以及对象移动的功能，进行拼摆活动，吸引学生的注意力。 2、我应用了电子白板的分层功能将3、4、12这几个数字进行重叠排序，拖动对象依次增加小正方形数量； 3、应用电子白板自带的垃圾桶，用于回收拼错的图形。 4、应用电子白板自带的答案核查工具反馈答案。 5、指名学生到白板前完成表格，利用白板的交互性，学生可以任意拖动数字，从而改变了以往的黑板板书形式。 6、利用电子白板的聚光灯功能，将学生的注意力集中到1和它本身这两个因数上，从而提高兴趣，加深印象，为分类奠定基础。 7、因学生在本节课前没有接触过因数个数这个概念，因此在观察表格时我利用了电子白板的白色画笔将因数个数一栏涂满覆盖，首先引导学生观察因数，待学生发现了因数中的有关信息后再引导学生从因数个数的角度考虑。 8、利用红色画笔在白板上即时书写，反馈学生信息。
课 件 截 图
教学 环节 教学内容 活动设计 设计意图 媒体使用及分析（交互式电子白板的使用功能）
应 用 概 念 ， 巩 固 拓 展 1、判断一个数是质数还是合数（50以内的数） 利用学号牌上的数字进行全班互动，鼓励每个学生动脑想，动口说，最后总结方法。 2、对100以内的数字进行筛选判断，找出所有质数，做一张质数表。 1、拿出课前随机发放的学号牌，指名学生到讲台前介绍自己的学号。它是质数还是合数？怎么判断？ 2、总结出判断质数和合数的方法：不需要找出它的所有因数，只要找到除了1和它本身外，是否还有第三个因数即可。 3、质数的学生起立，合数的学生起立。再次渗透1既不是质数也不是合数。 1、在学生掌握了质数和合数概念的基础上，利用判断学号是质数还是合数巩固概念，全班互动的形式不仅可以在新课结束后活跃课堂气氛，同时也可进一步巩固新知，全班总结出判断质数和合数的方法，激发学生进一步探索和研究的欲望。 2、由学号牌上50以内的数字再到制作100以内的质数表，体现了数学由易到难，由浅入深的理念。 1、在制作100以内质数表的环节，利用电子白板的荧光笔划去不是质数的数字，可以即时反馈学生答案，具备了以往多媒体所没有的交互性。
课 件 截 图
教学 环节 教学内容 活动设计 设计意图 媒体使用及分析（交互式电子白板的使用功能）
分 层 练 习 ， 概 念 升 华 1、基础练习 2、拓展练习 3、开放练习 随机选号，判断质数还是合数，比一比谁的反应快。 猜一猜（拓展练习） 3、想一想（开放练习） 4=（ ）+（ ） 6=（ ）+（ ） 8=（ ）+（ ） 10=（ ）+（ ） （ ）=（ ）+（ ） 通过设计不同类型不同层次的练习，不仅可以达到巩固新知的作用，同时给不同层次的学生展示自己的机会，使个学生都参与到课堂中来。 1、练习主要是考察学生对概念的理解。利用白板中自带的随机数生成工具提高学生的兴趣，再次巩固质数合数的概念及判断质数合数的方法。 2、利用翻板工具使课堂更加灵活多变，生动有趣，生可以根据自己的能力随机选择题目作答。 3、开放题是基于“哥德巴赫猜想”而设计的，通过开放性的练习，给学生思维发散的机会。
课 件 截 图
课 件 截 图
教学 环节 教学内容 活动设计 设计意图 媒体使用及分析（交互式电子白板的使用功能）
课 堂 总 结 ， 课 后 延 伸 哥德巴赫猜想是世界近代三大数学难题之一。1742年，由德国数学家哥德巴赫首次提出。这道题看似简单，要想证明却非常困难，成为数学中一个著名的难题，被称为“数学王冠上的明珠”。 世界各国的数学家都想攻克这道难题，但至今还未解决。 展示哥德巴赫猜想简介 提出期望：感兴趣的同学课下可以利用今天所学的知识去研究一下哥德巴赫猜想，希望有朝一日你们能够真正地摘取这颗数学王冠上的明珠！ 介绍古今中外人们对质数与合数的研究和探索，不仅激发了学生的求知欲望，同时也渗透了人类对有关质数问题探索情况。有利于渗透学生对数学文化的了解，提高学生探索数学问题的兴趣。 利用对象动画淡入陈景润图片。
课 件 截 图