五年级下册数学课件 长方体和正方体的体积 人教版(共17页PPT)
文档属性
| 名称 | 五年级下册数学课件 长方体和正方体的体积 人教版(共17页PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 508.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-05 22:01:04 | ||
图片预览

文档简介
(共17张PPT)
长方体和正方体
第5课时
长方体和正方体的体积
一、情境导入
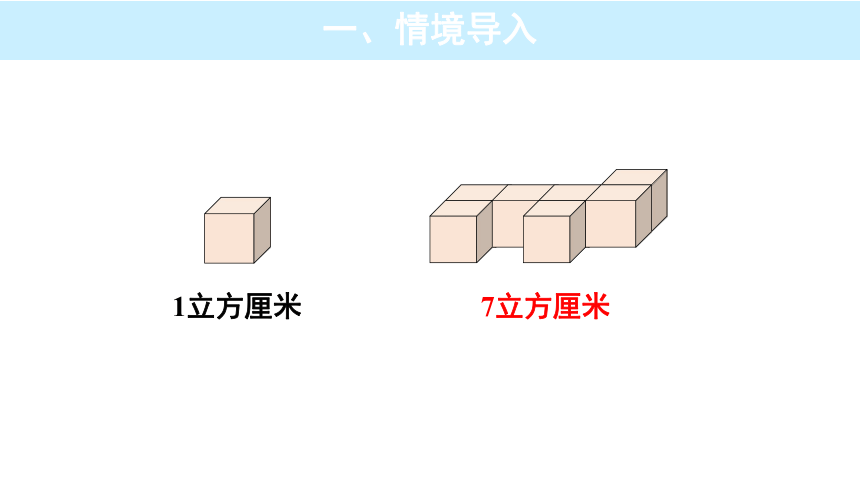
7立方厘米
1立方厘米
一、情境导入
怎样知道一个长方体的体积呢?
如果能把它切成一些小正方体就好了。
能不能先测量,再计算出体积呢?
二、探究新知
长 宽 高 小正方体的数量 长方体的体积
用12个体积为1 cm3的小正方体摆出不同的长方体。
二、探究新知
用12个体积为1 cm3的小正方体摆出不同的长方体。
二、探究新知
二、探究新知
二、探究新知
二、探究新知
长 宽 高 小正方体的数量 长方体的体积
4 cm
1 cm
3 cm
12
12 cm3
3 cm
2 cm
2 cm
12
12 cm3
6 cm
1 cm
2 cm
12
12 cm3
用12个体积为1 cm3的小正方体摆出不同的长方体。
二、探究新知
长方体的体积=
长×宽×高
V=abh
正方体的体积=
棱长×棱长×棱长
V=a · a · a
a表示棱长,a3读作a的立方,表示3个a相乘。
二、探究新知
V=abh
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
7 cm
3 cm
4 cm
6 dm
6 dm
6 dm
二、探究新知
长方体或正方体底面的面积叫底面积。
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
二、探究新知
长方体和正方体的体积也可以这样来计算:
长方体(或正方体)的体积=底面积×高
如果用字母S表示底面积,上面的公式可以写成:V=Sh
三、巩固练习
1.一块长方体肥皂的长15 cm、宽7 cm、高8 cm。它的体积是多少?
V=abh=15×7×8=840(cm3)
答:它的体积是840立方厘米。
三、巩固练习
2.一块棱长30厘米的正方体冰块,它的体积是多少立方厘米?
V=a3=30×30×30=27000(cm3)
答:它的体积是27000立方厘米。
三、巩固练习
3.建筑工地要挖一个长50米、宽30米、深50厘米的长方体土坑,一共要挖出多少方的土?(在工程上,1立方米的土、沙、石等均简称“1方”)
50厘米=0.5米
V=abh=50×30×0.5=750(m3)
答:一共要挖出750方的土。
四、课堂小结
1.长方体的体积=长×宽×高
V=abh
2.正方体的体积=棱长×棱长×棱长
V=a3
3.长方体(或正方体)的体积=底面积×高
V=Sh
长方体和正方体
第5课时
长方体和正方体的体积
一、情境导入
7立方厘米
1立方厘米
一、情境导入
怎样知道一个长方体的体积呢?
如果能把它切成一些小正方体就好了。
能不能先测量,再计算出体积呢?
二、探究新知
长 宽 高 小正方体的数量 长方体的体积
用12个体积为1 cm3的小正方体摆出不同的长方体。
二、探究新知
用12个体积为1 cm3的小正方体摆出不同的长方体。
二、探究新知
二、探究新知
二、探究新知
二、探究新知
长 宽 高 小正方体的数量 长方体的体积
4 cm
1 cm
3 cm
12
12 cm3
3 cm
2 cm
2 cm
12
12 cm3
6 cm
1 cm
2 cm
12
12 cm3
用12个体积为1 cm3的小正方体摆出不同的长方体。
二、探究新知
长方体的体积=
长×宽×高
V=abh
正方体的体积=
棱长×棱长×棱长
V=a · a · a
a表示棱长,a3读作a的立方,表示3个a相乘。
二、探究新知
V=abh
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
7 cm
3 cm
4 cm
6 dm
6 dm
6 dm
二、探究新知
长方体或正方体底面的面积叫底面积。
底面
底面
长方体的体积=长×宽×高
底面积
正方体的体积=棱长×棱长×棱长
底面积
二、探究新知
长方体和正方体的体积也可以这样来计算:
长方体(或正方体)的体积=底面积×高
如果用字母S表示底面积,上面的公式可以写成:V=Sh
三、巩固练习
1.一块长方体肥皂的长15 cm、宽7 cm、高8 cm。它的体积是多少?
V=abh=15×7×8=840(cm3)
答:它的体积是840立方厘米。
三、巩固练习
2.一块棱长30厘米的正方体冰块,它的体积是多少立方厘米?
V=a3=30×30×30=27000(cm3)
答:它的体积是27000立方厘米。
三、巩固练习
3.建筑工地要挖一个长50米、宽30米、深50厘米的长方体土坑,一共要挖出多少方的土?(在工程上,1立方米的土、沙、石等均简称“1方”)
50厘米=0.5米
V=abh=50×30×0.5=750(m3)
答:一共要挖出750方的土。
四、课堂小结
1.长方体的体积=长×宽×高
V=abh
2.正方体的体积=棱长×棱长×棱长
V=a3
3.长方体(或正方体)的体积=底面积×高
V=Sh
