五年级下册数学课件 长方体和正方体的体积 冀教版(共78张PPT)
文档属性
| 名称 | 五年级下册数学课件 长方体和正方体的体积 冀教版(共78张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 00:00:00 | ||
图片预览








文档简介
(共78张PPT)
1 体积和体积单位
第1课时 认识体积和体积单位(教材P56~58)
五年级数学·下 新课标[冀教] 第5单元
你知道乌鸦为什么喝到水了吗?
1.一个瓶颈高的瓶子装了半瓶水,乌鸦喝不到水。
2.乌鸦用嘴叼石子放入瓶中,水面慢慢升高了。
3.乌鸦可以喝到水了。
难点点拨
因为小石子占据了一定的空间,所以导致水面上升。
小实验。
(1)取两个同样的玻璃杯,放入同样多的水(可在
水中滴一滴墨水)。
(2)把一个土豆和一块小石头分别放入两个杯中。
两个玻璃杯中的水面发生了什么变化?说明了什么?
把土豆和石子放在杯子里
升的高一些
升的矮一些
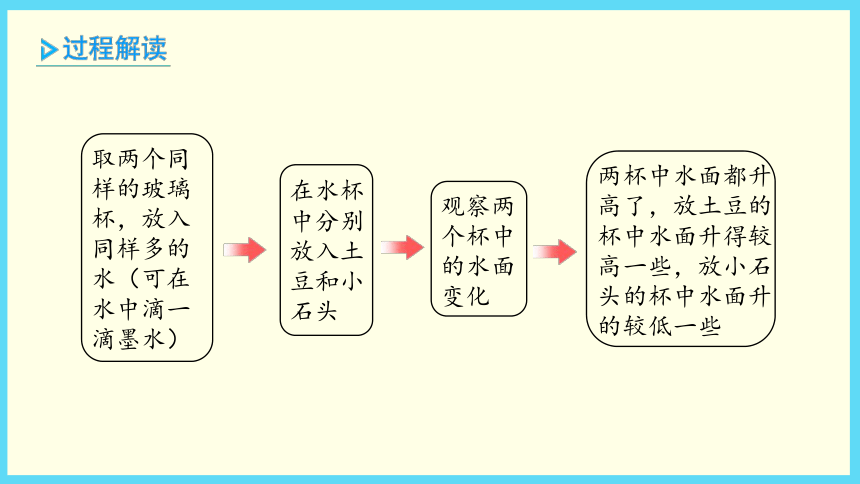
取两个同样的玻璃杯,放入同样多的水(可在水中滴一滴墨水)
在水杯中分别放入土豆和小石头
观察两个杯中的水面变化
两杯中水面都升高了,放土豆的杯中水面升得较高一些,放小石头的杯中水面升的较低一些
放土豆的玻璃杯水面上升得比放小石头的高,说明土豆比小石头占的地方大,小石头占的空间小,土豆占的空间大。从上面实验中可知物体都占据着一定的空间,物体大则占据的空间大,物体小则占据的空间小。
规范解答
物体所占空间的大小叫做物体的体积。
要点提示
把一个物体放入盛水的容器里(物体没入水中,水未溢出),上升的水的体积就是所放入的物体的体积。
难点点拨
物体所占空间越大,体积就越大,物体所占空间越小,体积就越小。
3
测量长度要用到长度单位
测量面积要用到面积单位
测量体积要用到体积单位
常用的长度单位:米、分米、厘米;
常用的面积单位:平方米、平方分米、平方厘米;
常用的体积单位有立方米、立方分米和立方厘米。
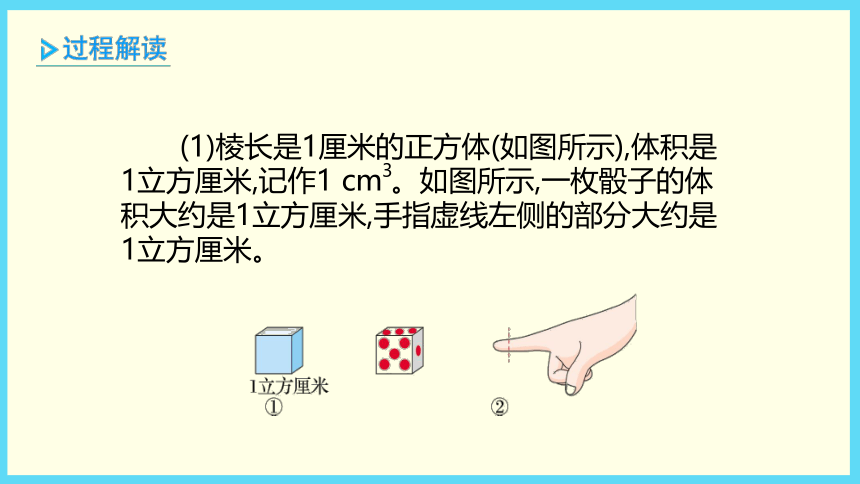
(1)棱长是1厘米的正方体(如图所示),体积是1立方厘米,记作1 cm 。如图所示,一枚骰子的体积大约是1立方厘米,手指虚线左侧的部分大约是1立方厘米。
3
(2)棱长是1分米的正方体,体积是1立方分米,记作1 dm 。如图所示,一个粉笔盒的体积接近1立方分米。
3
(3)棱长是1米的正方体,体积是1立方米,记作1 m 。如图所示,用3根1米长的木条可以在墙角搭成一个1立方米的空间。
3
计量一个物体的体积,要看这个物体含有多少个体积单位。例如,下图的长方体是用4个1立方厘米的小正方体拼成的,它的体积就是4立方厘米。
简单应用
常用的体积单位有立方厘米、立方分米、立方米。计量一个物体的体积,要看这个物体含有多少个体积单位。
难点点拨
棱长为1 cm的正方体的体积是1 cm3,但体积是1 cm3的物体不一定就是棱长为1 cm的正方体。
1 体积和体积单位
第2课时 长方体的体积公式及
体积计算(教材P59~60)
五年级数学·下 新课标[冀教] 第5单元
冰箱的占地空间有多大?
就是求冰箱的体积。
小组合作,用40个1立方厘米的小正方体,分别搭出不同的长方体,并填写下表。
图号 长(厘米) 宽(厘米) 高(厘米) 体积(立方厘米)
① 10 4 1 40
② 5 4 2 40
③
④
长方体的体积与它的长、宽、高有什么关系?
图号 长(厘米) 宽(厘米) 高(厘米) 体积(立方厘米)
① 10 4 1 40
② 5 4 2 40
③
④
填写表格,明确长方体体积
10
2
2
40
8
5
1
40
图号 长(厘米) 宽(厘米) 高(厘米) 体积(立方厘米)
① 10 4 1 40
② 5 4 2 40
③ 10 2 2 40
④ 8 5 1 40
观察表格,推导公式
发现:10×4×1=40 10×2×2=40
5×4×2=40 8×5×1=40
得出:长方体所含小正方体的数量就是长方体的体积。
小正方体的数量
每行个数
行数
层数
=
×
×
长方体的体积
长
宽
高
=
×
×
用字母表示为V=abh
长方体的体积=长×宽×高,用字母表示为V=abh。
一块砖的长是24厘米,宽是12厘米,厚是6厘米。它的体积是多少立方厘米?
先估计一下,再计算。
砖的长
砖的宽
砖的高(厚)
砖的体积
×
×
=
(1)估计砖的体积 估计长、宽、高分别为25厘米、10厘米、5厘米,利用公式计算25×10×5=1250(立方厘米)。
(2)实际计算
已知砖的长、宽、厚(也就是高)求体积,可直接代入公式计算。
24×12×6=288×6=1728(立方厘米)
答:它的体积是1728立方厘米。
规范解答
知道长方体的长、宽、高,直接应用公式就能求出它的体积。
1 体积和体积单位
第3课时 正方体的体积公式及长方体、
正方体体积计算的一般公式(教材P61~62)
五年级数学·下 新课标[冀教] 第5单元
同步练习
4块
2块
3块
4×3×2
= 12×2
= 24(块)
答:可以切24块。
把一个长4分米,宽3分米,高2分米的长方体木块切成棱长是1分米的小正方体木块,可以切几块。
计算下面正方体的体积。
用长方体的体积公式能计算正方体的体积吗?为什么?
(1)正方体和长方体的关系
正方体是特殊的长方体,即正方体是长、宽、高都相等的长方体。
(2)正方体体积公式的推导
长方体的体积
长
宽
高
=
×
×
正方体的体积
棱长
棱长
棱长
=
×
×
(3)正方体体积公式的字母表达式
如果用V 表示正方体的体积,用 a 表示它的棱长,那么正方体的体积公式可以写成:
V=a ×a×a=a ·a ·a=a3。a3 读作“a 的立方”,表示三个a 相乘。
3×3×3=27(cm )
答:正方体的体积是27 cm 。
规范解答
3
3
正方体的体积=棱长×棱长×棱长,用字母表示为V =a3。
长方体和正方体的体积公式有什么相同点?
无论将长方体或正方体怎样放置,总有一个面在下面,通常把下面的面叫做底面,底面的面积叫做底面积,如图。
(1) 观察长方体、正方体
(2)底面积的计算
长方体的底面积=长×宽,
正方体的底面积=棱长×棱长。
高
长方体的体积
长×宽
×
=
(3)体积公式的推导
底面积
正方体的体积
棱长
棱长
棱长
=
×
×
底面积
可以看成是高
长方体(或正方体)的体积=底面积×高
长方体(或正方体)的体积=底面积×高,h表示高,则字母表达式为V=Sh。
易混淆警示
长方体放置的方式不同,底面就不同,所以求底面积时,一定要找准底面的长和宽。
一根长方体木料,长是5米,横断面的面积是0.06平方米。15根这样的木料的体积是多少立方米?
3
先求什么,再求什么?
规范解答
先求一根木料的体积
再求15根木料的体积
0.06×5=0.3(立方米) 0.3×15=4.5(立方米)
答:15根这样的木料的体积是4.5立方米。
长方体、正方体的体积公式根据实际情况,灵活运用。
巧学妙记
面积体积大不同,
相邻三面和乘二,
就是来求表面积。
相邻三棱积是体,
还有底面来乘高。
巧学妙记
面积体积大不同,
相邻三面和乘二,
就是来求表面积。
相邻三棱积是体,
还有底面来乘高。
1 体积和体积单位
第4课时 体积单位之间的进率(教材P63~64)
五年级数学·下 新课标[冀教] 第5单元
求洗衣机包装箱的体积。
长、宽、高的单位是什么?
包装箱上标有80×50×90,表示包装箱的长是80厘米,宽是50厘米,高是90厘米,长、宽、高的单位是厘米。
也可以说包装箱的长是8分米,宽是5分米,高是9分米。
(1)80×50×90=360000(立方厘米)。
(2)8×5×9=360(立方分米)。
规范解答
长方体的体积=长×宽×高。
计算同一个包装箱,体积单位不同,计算出的数也不一样,用厘米作单位,计算出的数大,用分米作单位,计算出的数小,但计算结果相同,也就是说:360000立方厘米=360立方分米。
观察、比较两个算式
运用的单位不同,计算出的数也不一样。
1立方分米等于多少立方厘米?
探究dm 和cm 的关系
3
3
沿图(3)的一条棱可以摆放10个棱长为1cm的小正方体,如图(1)
沿另一条棱可以摆放10行,一共可放(10×10)个,如图(2)
沿着高可以摆放10层,一共可以摆放(10×10×10)个
棱长为1dm的正方体体积
棱长为10cm的正方体体积
=
1×1×1=1(dm )
3
10×10×10=1000(dm )
3
1dm =1000cm
3
3
探究m 和dm 之间的关系
3
3
根据上面的推导方法,可以得出1 m3=1000 dm3。
相邻的体积单位之间的进率是1000,
1立方米=1000立方分米,
1立方分米=1000立方厘米。
求2.5 dm3等于多少立方厘米,是高级单位(大单位)改写成低级单位(小单位)。
求8500 dm3等于多少立方米,是低级单位(小单位)改写成高级单位(大单位)。
3
2.5 dm3=( )cm3,8500 dm3=( )m3。
规范解答
2.5 dm3=( )cm3,8500 dm3=( )m3。
×进率(1000)
高 低
低 高
÷进率(1000)
2500
8.5
体积单位之间互化的方法:由低级单位改写成高级单位,用低级单位的数除以进率。由高级单位改写成低级单位,用高级单位的数乘进率。
2 应用问题
第1课时 简单的土石方计算
问题(教材P65)
五年级数学·下 新课标[冀教] 第5单元
新课导入
想一想,填一填。
80立方分米=( )立方米 3立方米=( )立方分米
0.6立方米=( )立方厘米
0.08
3000
600000
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
理解题意
求要挖出多少立方米的土,就是求长2米、宽1.6米、高1.5米的长方体地窖的体积。
“深”指的是长方体地窖的高。
规范解答
根据“长方体的体积=长×宽×高”列式解答:
2×1.6×1.5=4.8(立方米)。
答:要挖出4.8立方米的土。
了解“方”的含义
生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。本题中4.8立方米的土也可以说4.8方的土,即4.8立方米=4.8方。
生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”,换算如下:1方=1立方米=1000立方分米=1000000立方厘米。
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这条拦河坝一共需要土石多少方?
理解题意
拦河坝的体积=横断面面积×长,在这里横断面的面积可以看作底面积,拦河坝的长可以看作高。
求修这条拦河坝一共需要多少方土石就是求这个拦河坝的体积。
拦河坝体积的计算方法
规范解答
横断面面积:(8+3)×4÷2=22(平方米)
土石的体积:22×50=1100(方)
答:修这条拦河坝一共需要土石1100方。
根据“(上底+下底)×高÷2”求出横断面面积,再乘长,即得体积。
2 应用问题
第2课时 容积和容积的计算(教材P67~68)
五年级数学·下 新课标[冀教] 第5单元
新课导入
在《左传》《周礼》《仪礼》《尔雅》等经典著作中都有关于容积单位的记载,其专用名称有升、斗、斛、豆、区、釜、钟以及溢、掬等。同长度一样,周代以前容积也是用人的身体计量,以一手所能盛的叫做溢,两手合盛的叫做掬,掬是最初的基本容积单位。
古代的容积单位
新课导入
《小尔雅·广量》中说“掬四谓之豆”,《左传·昭公三年》中说“四升为豆”,这两种说法是相通的,就是说掬也就是升,所以升(也就是掬)是容积的基本单位。后来《汉书·律历志》对容积单位做了系统的整理,命名为龠、合、升、斗、斛五量,一合等于二龠,合以上都是十进制。升是容积的基本单位,斗和斛则为实用单位。
一个带盖的长方体木箱,从外面测量的尺寸如图①所示。(单位:米)这个木箱的体积大约是多少立方米?
已知木板的厚度是0.025米(如图②所示)。如果在里面装满小麦,那么能装多少立方米小麦?
怎样计算箱子的容积? 计算体积和容积有什么相同点和不同点?
计算木箱的体积
已知木箱的长、宽、高,求体积。根据“长方体的体积=长×宽×高”求解。
1.25×0.55×0.45=0.309375(立方米)
0.309375立方米≈0.31立方米(取近似值,保留两位小数)
答:这个木箱的体积大约是0.31立方米。
“深”指的是长方体地窖的高。
认识容积
用从外面测量的长、宽、高减去木板的厚度,就能求出从里面测量的长、宽、高各是多少。
算出木箱里面的长、宽、高,再用长×宽×高求容积。
在数学上,箱子所能容纳物体的体积,通常叫做容积。本题要求能装多少立方米的小麦,就是求木箱里面的体积,也就是容积。
计算木箱的容积
规范解答
木箱里面的长:1.25-0.025×2=1.2(米)
木箱里面的宽:0.55-0.025×2=0.5(米)
木箱里面的高:0.45-0.025×2=0.4(米)
木箱的容积:1.2×0.5×0.4=0.24(立方米)。
答:能装0.24立方米小麦。
计量容积也可以用体积单位,尤其是计量容器装固体多少时,常用体积单位。
比较体积和容积的异同
相同点:都用长×宽×高这个公式来计算。
不同点:计算体积的数据是从外面测量的,计算容积的数据是从里面测量的。
1.容积和体积的计算方法相同,但尺寸取法不同,计算容积要从里面测量数据。
2.容积的大小是通过容器所能容纳物体的体积显示出来的,容积和体积意义不同。
一个长方体水箱,从里面测量得到长、宽、高的数据如下图:
(1)这个长方体水箱的容积是多少立方分米?
(1)计算水箱的容积
因为题中给出了从里面测量水箱长、宽、高的数据,所以水箱的容积可以直接利用公式计算。
5×4×3=20×3=60(立方分米)
答:这个长方体水箱的容积是60立方分米。
认识计量液体体积时的常用单位
所以水箱的容积是60升。
在一般情况下,计算容积用体积单位就可以了,但当计量液体的体积时,我们通常用“升”和“毫升”作单位,且
(2)如果这个水箱装有 的水,那么水箱中的水有多少升?
3
5
计算水的体积
3
5
因为水箱只装了 的水,所以水的体积等于水箱容积的 。
3
5
3
5
60× =36(立方分米),36立方分米=36升。
3
5
答:如果这个水箱装有 的水,那么水箱中的水有36升。
2. 1升=1立方分米 1毫升=1立方厘米。
1.计量容积一般用体积单位,但计量液体的体积通常用“毫升”“升”作单位。
再
见
1 体积和体积单位
第1课时 认识体积和体积单位(教材P56~58)
五年级数学·下 新课标[冀教] 第5单元
你知道乌鸦为什么喝到水了吗?
1.一个瓶颈高的瓶子装了半瓶水,乌鸦喝不到水。
2.乌鸦用嘴叼石子放入瓶中,水面慢慢升高了。
3.乌鸦可以喝到水了。
难点点拨
因为小石子占据了一定的空间,所以导致水面上升。
小实验。
(1)取两个同样的玻璃杯,放入同样多的水(可在
水中滴一滴墨水)。
(2)把一个土豆和一块小石头分别放入两个杯中。
两个玻璃杯中的水面发生了什么变化?说明了什么?
把土豆和石子放在杯子里
升的高一些
升的矮一些
取两个同样的玻璃杯,放入同样多的水(可在水中滴一滴墨水)
在水杯中分别放入土豆和小石头
观察两个杯中的水面变化
两杯中水面都升高了,放土豆的杯中水面升得较高一些,放小石头的杯中水面升的较低一些
放土豆的玻璃杯水面上升得比放小石头的高,说明土豆比小石头占的地方大,小石头占的空间小,土豆占的空间大。从上面实验中可知物体都占据着一定的空间,物体大则占据的空间大,物体小则占据的空间小。
规范解答
物体所占空间的大小叫做物体的体积。
要点提示
把一个物体放入盛水的容器里(物体没入水中,水未溢出),上升的水的体积就是所放入的物体的体积。
难点点拨
物体所占空间越大,体积就越大,物体所占空间越小,体积就越小。
3
测量长度要用到长度单位
测量面积要用到面积单位
测量体积要用到体积单位
常用的长度单位:米、分米、厘米;
常用的面积单位:平方米、平方分米、平方厘米;
常用的体积单位有立方米、立方分米和立方厘米。
(1)棱长是1厘米的正方体(如图所示),体积是1立方厘米,记作1 cm 。如图所示,一枚骰子的体积大约是1立方厘米,手指虚线左侧的部分大约是1立方厘米。
3
(2)棱长是1分米的正方体,体积是1立方分米,记作1 dm 。如图所示,一个粉笔盒的体积接近1立方分米。
3
(3)棱长是1米的正方体,体积是1立方米,记作1 m 。如图所示,用3根1米长的木条可以在墙角搭成一个1立方米的空间。
3
计量一个物体的体积,要看这个物体含有多少个体积单位。例如,下图的长方体是用4个1立方厘米的小正方体拼成的,它的体积就是4立方厘米。
简单应用
常用的体积单位有立方厘米、立方分米、立方米。计量一个物体的体积,要看这个物体含有多少个体积单位。
难点点拨
棱长为1 cm的正方体的体积是1 cm3,但体积是1 cm3的物体不一定就是棱长为1 cm的正方体。
1 体积和体积单位
第2课时 长方体的体积公式及
体积计算(教材P59~60)
五年级数学·下 新课标[冀教] 第5单元
冰箱的占地空间有多大?
就是求冰箱的体积。
小组合作,用40个1立方厘米的小正方体,分别搭出不同的长方体,并填写下表。
图号 长(厘米) 宽(厘米) 高(厘米) 体积(立方厘米)
① 10 4 1 40
② 5 4 2 40
③
④
长方体的体积与它的长、宽、高有什么关系?
图号 长(厘米) 宽(厘米) 高(厘米) 体积(立方厘米)
① 10 4 1 40
② 5 4 2 40
③
④
填写表格,明确长方体体积
10
2
2
40
8
5
1
40
图号 长(厘米) 宽(厘米) 高(厘米) 体积(立方厘米)
① 10 4 1 40
② 5 4 2 40
③ 10 2 2 40
④ 8 5 1 40
观察表格,推导公式
发现:10×4×1=40 10×2×2=40
5×4×2=40 8×5×1=40
得出:长方体所含小正方体的数量就是长方体的体积。
小正方体的数量
每行个数
行数
层数
=
×
×
长方体的体积
长
宽
高
=
×
×
用字母表示为V=abh
长方体的体积=长×宽×高,用字母表示为V=abh。
一块砖的长是24厘米,宽是12厘米,厚是6厘米。它的体积是多少立方厘米?
先估计一下,再计算。
砖的长
砖的宽
砖的高(厚)
砖的体积
×
×
=
(1)估计砖的体积 估计长、宽、高分别为25厘米、10厘米、5厘米,利用公式计算25×10×5=1250(立方厘米)。
(2)实际计算
已知砖的长、宽、厚(也就是高)求体积,可直接代入公式计算。
24×12×6=288×6=1728(立方厘米)
答:它的体积是1728立方厘米。
规范解答
知道长方体的长、宽、高,直接应用公式就能求出它的体积。
1 体积和体积单位
第3课时 正方体的体积公式及长方体、
正方体体积计算的一般公式(教材P61~62)
五年级数学·下 新课标[冀教] 第5单元
同步练习
4块
2块
3块
4×3×2
= 12×2
= 24(块)
答:可以切24块。
把一个长4分米,宽3分米,高2分米的长方体木块切成棱长是1分米的小正方体木块,可以切几块。
计算下面正方体的体积。
用长方体的体积公式能计算正方体的体积吗?为什么?
(1)正方体和长方体的关系
正方体是特殊的长方体,即正方体是长、宽、高都相等的长方体。
(2)正方体体积公式的推导
长方体的体积
长
宽
高
=
×
×
正方体的体积
棱长
棱长
棱长
=
×
×
(3)正方体体积公式的字母表达式
如果用V 表示正方体的体积,用 a 表示它的棱长,那么正方体的体积公式可以写成:
V=a ×a×a=a ·a ·a=a3。a3 读作“a 的立方”,表示三个a 相乘。
3×3×3=27(cm )
答:正方体的体积是27 cm 。
规范解答
3
3
正方体的体积=棱长×棱长×棱长,用字母表示为V =a3。
长方体和正方体的体积公式有什么相同点?
无论将长方体或正方体怎样放置,总有一个面在下面,通常把下面的面叫做底面,底面的面积叫做底面积,如图。
(1) 观察长方体、正方体
(2)底面积的计算
长方体的底面积=长×宽,
正方体的底面积=棱长×棱长。
高
长方体的体积
长×宽
×
=
(3)体积公式的推导
底面积
正方体的体积
棱长
棱长
棱长
=
×
×
底面积
可以看成是高
长方体(或正方体)的体积=底面积×高
长方体(或正方体)的体积=底面积×高,h表示高,则字母表达式为V=Sh。
易混淆警示
长方体放置的方式不同,底面就不同,所以求底面积时,一定要找准底面的长和宽。
一根长方体木料,长是5米,横断面的面积是0.06平方米。15根这样的木料的体积是多少立方米?
3
先求什么,再求什么?
规范解答
先求一根木料的体积
再求15根木料的体积
0.06×5=0.3(立方米) 0.3×15=4.5(立方米)
答:15根这样的木料的体积是4.5立方米。
长方体、正方体的体积公式根据实际情况,灵活运用。
巧学妙记
面积体积大不同,
相邻三面和乘二,
就是来求表面积。
相邻三棱积是体,
还有底面来乘高。
巧学妙记
面积体积大不同,
相邻三面和乘二,
就是来求表面积。
相邻三棱积是体,
还有底面来乘高。
1 体积和体积单位
第4课时 体积单位之间的进率(教材P63~64)
五年级数学·下 新课标[冀教] 第5单元
求洗衣机包装箱的体积。
长、宽、高的单位是什么?
包装箱上标有80×50×90,表示包装箱的长是80厘米,宽是50厘米,高是90厘米,长、宽、高的单位是厘米。
也可以说包装箱的长是8分米,宽是5分米,高是9分米。
(1)80×50×90=360000(立方厘米)。
(2)8×5×9=360(立方分米)。
规范解答
长方体的体积=长×宽×高。
计算同一个包装箱,体积单位不同,计算出的数也不一样,用厘米作单位,计算出的数大,用分米作单位,计算出的数小,但计算结果相同,也就是说:360000立方厘米=360立方分米。
观察、比较两个算式
运用的单位不同,计算出的数也不一样。
1立方分米等于多少立方厘米?
探究dm 和cm 的关系
3
3
沿图(3)的一条棱可以摆放10个棱长为1cm的小正方体,如图(1)
沿另一条棱可以摆放10行,一共可放(10×10)个,如图(2)
沿着高可以摆放10层,一共可以摆放(10×10×10)个
棱长为1dm的正方体体积
棱长为10cm的正方体体积
=
1×1×1=1(dm )
3
10×10×10=1000(dm )
3
1dm =1000cm
3
3
探究m 和dm 之间的关系
3
3
根据上面的推导方法,可以得出1 m3=1000 dm3。
相邻的体积单位之间的进率是1000,
1立方米=1000立方分米,
1立方分米=1000立方厘米。
求2.5 dm3等于多少立方厘米,是高级单位(大单位)改写成低级单位(小单位)。
求8500 dm3等于多少立方米,是低级单位(小单位)改写成高级单位(大单位)。
3
2.5 dm3=( )cm3,8500 dm3=( )m3。
规范解答
2.5 dm3=( )cm3,8500 dm3=( )m3。
×进率(1000)
高 低
低 高
÷进率(1000)
2500
8.5
体积单位之间互化的方法:由低级单位改写成高级单位,用低级单位的数除以进率。由高级单位改写成低级单位,用高级单位的数乘进率。
2 应用问题
第1课时 简单的土石方计算
问题(教材P65)
五年级数学·下 新课标[冀教] 第5单元
新课导入
想一想,填一填。
80立方分米=( )立方米 3立方米=( )立方分米
0.6立方米=( )立方厘米
0.08
3000
600000
李大伯计划挖一个长是2米、宽是1.6米、深是1.5米的地窖。要挖出多少立方米的土?
理解题意
求要挖出多少立方米的土,就是求长2米、宽1.6米、高1.5米的长方体地窖的体积。
“深”指的是长方体地窖的高。
规范解答
根据“长方体的体积=长×宽×高”列式解答:
2×1.6×1.5=4.8(立方米)。
答:要挖出4.8立方米的土。
了解“方”的含义
生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”。本题中4.8立方米的土也可以说4.8方的土,即4.8立方米=4.8方。
生活中,计量沙、土、石子等的体积时,常常把“立方米”简称为“方”,换算如下:1方=1立方米=1000立方分米=1000000立方厘米。
某村修一条50米长的拦河坝,拦河坝的横断面是一个梯形,尺寸如下图(单位:米)。修这条拦河坝一共需要土石多少方?
理解题意
拦河坝的体积=横断面面积×长,在这里横断面的面积可以看作底面积,拦河坝的长可以看作高。
求修这条拦河坝一共需要多少方土石就是求这个拦河坝的体积。
拦河坝体积的计算方法
规范解答
横断面面积:(8+3)×4÷2=22(平方米)
土石的体积:22×50=1100(方)
答:修这条拦河坝一共需要土石1100方。
根据“(上底+下底)×高÷2”求出横断面面积,再乘长,即得体积。
2 应用问题
第2课时 容积和容积的计算(教材P67~68)
五年级数学·下 新课标[冀教] 第5单元
新课导入
在《左传》《周礼》《仪礼》《尔雅》等经典著作中都有关于容积单位的记载,其专用名称有升、斗、斛、豆、区、釜、钟以及溢、掬等。同长度一样,周代以前容积也是用人的身体计量,以一手所能盛的叫做溢,两手合盛的叫做掬,掬是最初的基本容积单位。
古代的容积单位
新课导入
《小尔雅·广量》中说“掬四谓之豆”,《左传·昭公三年》中说“四升为豆”,这两种说法是相通的,就是说掬也就是升,所以升(也就是掬)是容积的基本单位。后来《汉书·律历志》对容积单位做了系统的整理,命名为龠、合、升、斗、斛五量,一合等于二龠,合以上都是十进制。升是容积的基本单位,斗和斛则为实用单位。
一个带盖的长方体木箱,从外面测量的尺寸如图①所示。(单位:米)这个木箱的体积大约是多少立方米?
已知木板的厚度是0.025米(如图②所示)。如果在里面装满小麦,那么能装多少立方米小麦?
怎样计算箱子的容积? 计算体积和容积有什么相同点和不同点?
计算木箱的体积
已知木箱的长、宽、高,求体积。根据“长方体的体积=长×宽×高”求解。
1.25×0.55×0.45=0.309375(立方米)
0.309375立方米≈0.31立方米(取近似值,保留两位小数)
答:这个木箱的体积大约是0.31立方米。
“深”指的是长方体地窖的高。
认识容积
用从外面测量的长、宽、高减去木板的厚度,就能求出从里面测量的长、宽、高各是多少。
算出木箱里面的长、宽、高,再用长×宽×高求容积。
在数学上,箱子所能容纳物体的体积,通常叫做容积。本题要求能装多少立方米的小麦,就是求木箱里面的体积,也就是容积。
计算木箱的容积
规范解答
木箱里面的长:1.25-0.025×2=1.2(米)
木箱里面的宽:0.55-0.025×2=0.5(米)
木箱里面的高:0.45-0.025×2=0.4(米)
木箱的容积:1.2×0.5×0.4=0.24(立方米)。
答:能装0.24立方米小麦。
计量容积也可以用体积单位,尤其是计量容器装固体多少时,常用体积单位。
比较体积和容积的异同
相同点:都用长×宽×高这个公式来计算。
不同点:计算体积的数据是从外面测量的,计算容积的数据是从里面测量的。
1.容积和体积的计算方法相同,但尺寸取法不同,计算容积要从里面测量数据。
2.容积的大小是通过容器所能容纳物体的体积显示出来的,容积和体积意义不同。
一个长方体水箱,从里面测量得到长、宽、高的数据如下图:
(1)这个长方体水箱的容积是多少立方分米?
(1)计算水箱的容积
因为题中给出了从里面测量水箱长、宽、高的数据,所以水箱的容积可以直接利用公式计算。
5×4×3=20×3=60(立方分米)
答:这个长方体水箱的容积是60立方分米。
认识计量液体体积时的常用单位
所以水箱的容积是60升。
在一般情况下,计算容积用体积单位就可以了,但当计量液体的体积时,我们通常用“升”和“毫升”作单位,且
(2)如果这个水箱装有 的水,那么水箱中的水有多少升?
3
5
计算水的体积
3
5
因为水箱只装了 的水,所以水的体积等于水箱容积的 。
3
5
3
5
60× =36(立方分米),36立方分米=36升。
3
5
答:如果这个水箱装有 的水,那么水箱中的水有36升。
2. 1升=1立方分米 1毫升=1立方厘米。
1.计量容积一般用体积单位,但计量液体的体积通常用“毫升”“升”作单位。
再
见
