北师大版数学九年级下册3.5 确定圆的条件 课件(22张ppt)
文档属性
| 名称 | 北师大版数学九年级下册3.5 确定圆的条件 课件(22张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览



文档简介
课件22张PPT。第三章
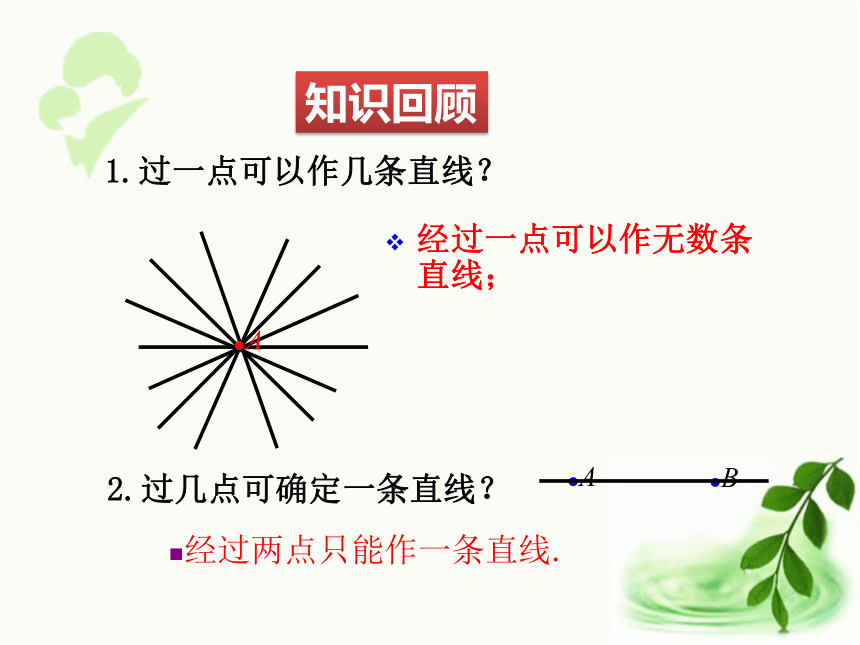
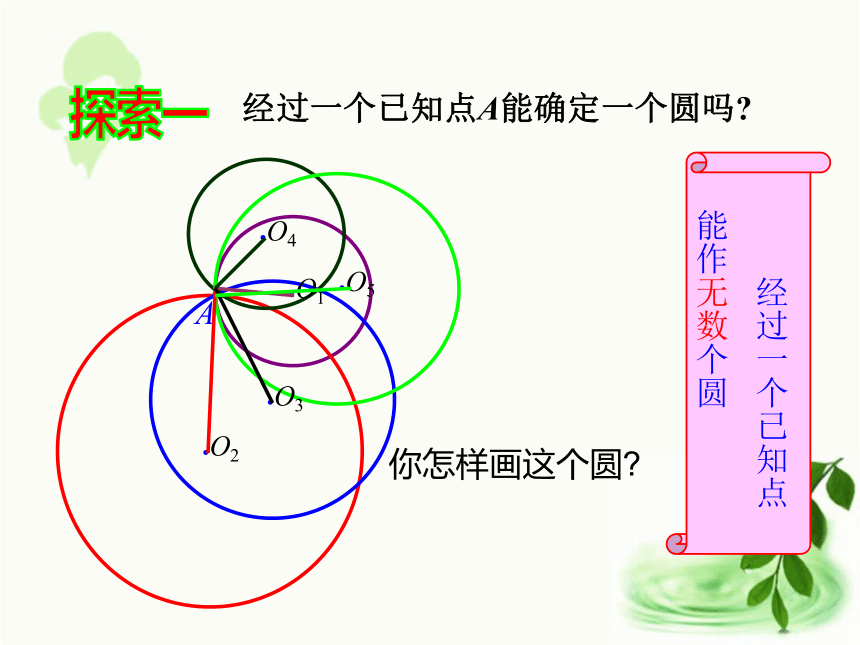
圆5 确定圆的条件北师大版数学九年级下册1.过一点可以作几条直线?经过一点可以作无数条直线;●A2.过几点可确定一条直线?经过两点只能作一条直线.●A●B知识回顾 过几点可以确定一个圆呢?思考:构成圆的基本要素有那些?两个条件:圆心半径探索新知探索一经过一个已知点A能确定一个圆吗?A 经过一个已知点
能作无数个圆
你怎样画这个圆?●O1●O2●O3●O5●O4探索二经过两个已知点A,B能确定一个圆吗?AB 经过两个已知点A,B能作无数个圆 经过两个已知点A,B所作的圆的圆心有什么规律?
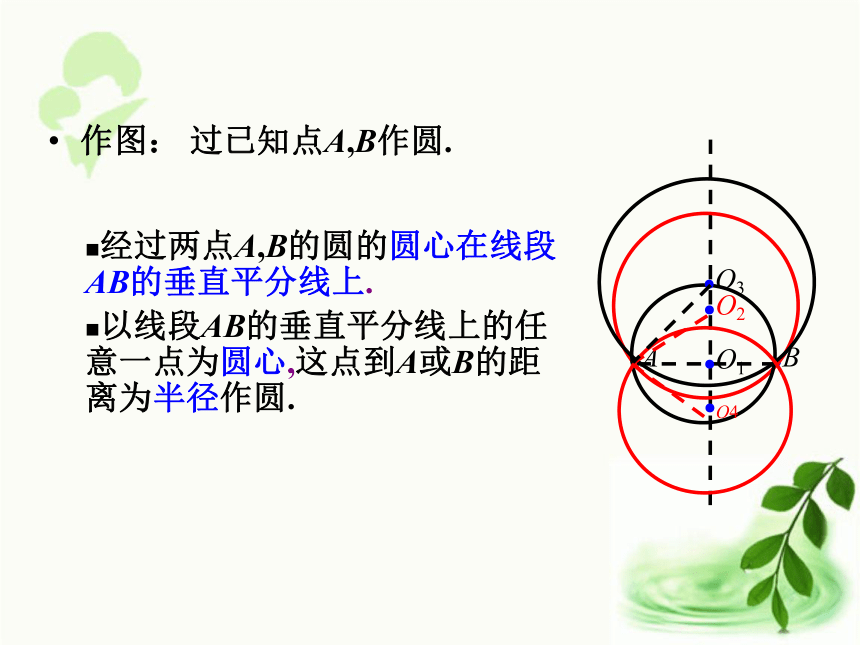
它们的圆心都在线段AB的垂直平分线上.作图: 过已知点A,B作圆.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
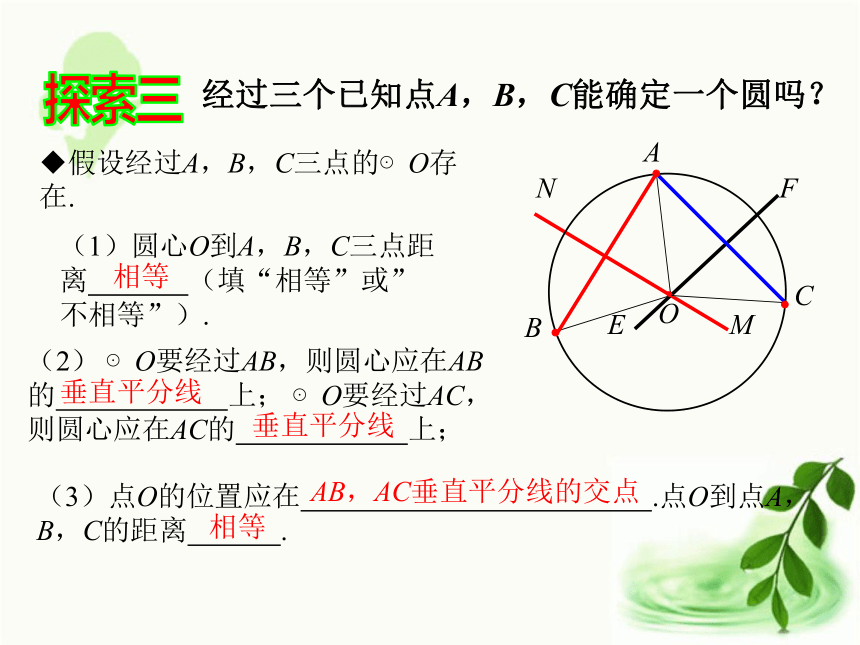
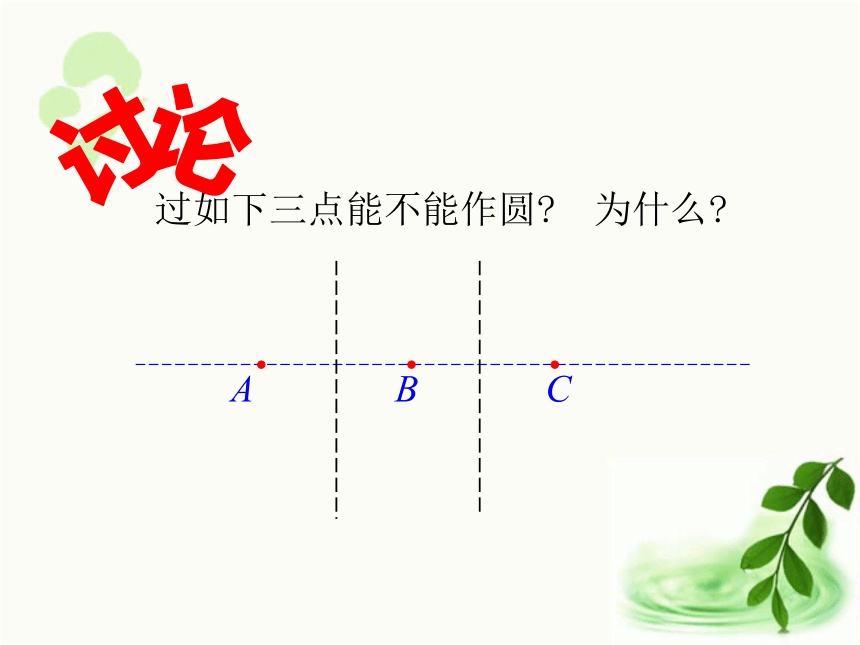
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.●A●B●O2●O1●O3●O4经过三个已知点A,B,C能确定一个圆吗?假设经过A,B,C三点的⊙O存在.(1)圆心O到A,B,C三点距离 (填“相等”或”不相等”).(2) ⊙O要经过AB,则圆心应在AB的 上; ⊙O要经过AC,则圆心应在AC的 上;(3)点O的位置应在 .点O到点A,B,C的距离 .NMFE相等垂直平分线垂直平分线相等AB,AC垂直平分线的交点探索三ABC过如下三点能不能作圆? 为什么?讨论画一画已知:不在同一直线上的三点A,B,C.
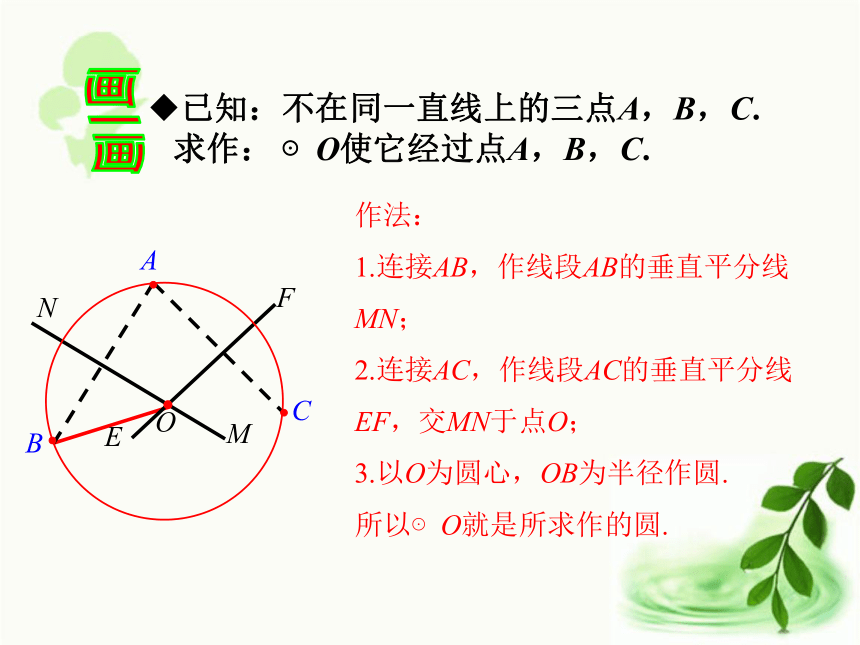
求作: ⊙O使它经过点A,B,C.作法:
1.连接AB,作线段AB的垂直平分线MN;
2.连接AC,作线段AC的垂直平分线EF,交MN于点O;
3.以O为圆心,OB为半径作圆.
所以⊙O就是所求作的圆.ONMFEABC定理:不在同一直线上的三点确定一个圆.定义 经过三角形各个顶点的圆叫作三角形的外接圆,外接圆的圆心叫作三角形的外心,这个三角形叫作圆的内接三角形.如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.外心是△ABC三条边的垂直平分线的交点,
它到三角形的三个顶点的距离相等.CABO三角形与圆的位置关系分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况.锐角三角形的外心位于三角形内
直角三角形的外心位于直角三角形斜边中点
注:(斜边长等于直径,圆的半径等于斜边的一半)
钝角三角形的外心位于三角形外.如何将一个如图所示的破损的圆盘复原?方法:
1.在圆弧上任取三点A,B,C.
2.作线段AB,BC的垂直平分线,其交点O即为圆心.
3.以点O为圆心,OC长为半径作圆.
⊙O即为所求.ABCO找一找如图,请找出图中圆的圆心,并写出你找圆心的方法?ABCO 某市要建一个圆形公园,要求公园刚好把动物园A,植物园B和人工湖C包括在内,又要使这个圆形的面积最小,请你给出这个公园的施工图.(A,B,C不在同一直线上)探究活动植物园动物园人工湖 图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心.C数学乐园·圆心练一练1.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
2.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是
A.重心 B.垂心 C.外心 D.无法确定.CBC随堂练习4.判断:
(1)经过三点一定可以作圆.( )
(2)三角形的外心就是这个三角形两边垂直平分线的交点.( )
(3)三角形的外心到三边的距离相等.( )
(4)等腰三角形的外心一定在这个三角形内.( )×√××5.在△ABC中,BC=24 cm,外心O到BC的距离为6 cm,求△ABC的外接圆半径 . 【归纳】等边三角形的外接圆的半径等于边长的( )倍.BCA思考:任意四个点是不是可以作一个圆?请举例说明. 不一定1. 四点在一条直线上不能作圆;3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.ABCDABCDABCDABCD2. 三点在同一直线上, 另一点不在这条直线上不能作圆;谈收获(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.(2)经过一个已知点能作无数个圆!(3)经过两个已知点A,B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上.(4)不在同一直线上的三个点确定一个圆.(5)外接圆,外心的概念.课堂小结谢谢!
圆5 确定圆的条件北师大版数学九年级下册1.过一点可以作几条直线?经过一点可以作无数条直线;●A2.过几点可确定一条直线?经过两点只能作一条直线.●A●B知识回顾 过几点可以确定一个圆呢?思考:构成圆的基本要素有那些?两个条件:圆心半径探索新知探索一经过一个已知点A能确定一个圆吗?A 经过一个已知点
能作无数个圆
你怎样画这个圆?●O1●O2●O3●O5●O4探索二经过两个已知点A,B能确定一个圆吗?AB 经过两个已知点A,B能作无数个圆 经过两个已知点A,B所作的圆的圆心有什么规律?
它们的圆心都在线段AB的垂直平分线上.作图: 过已知点A,B作圆.经过两点A,B的圆的圆心在线段AB的垂直平分线上.
以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.●A●B●O2●O1●O3●O4经过三个已知点A,B,C能确定一个圆吗?假设经过A,B,C三点的⊙O存在.(1)圆心O到A,B,C三点距离 (填“相等”或”不相等”).(2) ⊙O要经过AB,则圆心应在AB的 上; ⊙O要经过AC,则圆心应在AC的 上;(3)点O的位置应在 .点O到点A,B,C的距离 .NMFE相等垂直平分线垂直平分线相等AB,AC垂直平分线的交点探索三ABC过如下三点能不能作圆? 为什么?讨论画一画已知:不在同一直线上的三点A,B,C.
求作: ⊙O使它经过点A,B,C.作法:
1.连接AB,作线段AB的垂直平分线MN;
2.连接AC,作线段AC的垂直平分线EF,交MN于点O;
3.以O为圆心,OB为半径作圆.
所以⊙O就是所求作的圆.ONMFEABC定理:不在同一直线上的三点确定一个圆.定义 经过三角形各个顶点的圆叫作三角形的外接圆,外接圆的圆心叫作三角形的外心,这个三角形叫作圆的内接三角形.如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.外心是△ABC三条边的垂直平分线的交点,
它到三角形的三个顶点的距离相等.CABO三角形与圆的位置关系分别作出锐角三角形,直角三角形,钝角三角形的外接圆,并说明与它们外心的位置情况.锐角三角形的外心位于三角形内
直角三角形的外心位于直角三角形斜边中点
注:(斜边长等于直径,圆的半径等于斜边的一半)
钝角三角形的外心位于三角形外.如何将一个如图所示的破损的圆盘复原?方法:
1.在圆弧上任取三点A,B,C.
2.作线段AB,BC的垂直平分线,其交点O即为圆心.
3.以点O为圆心,OC长为半径作圆.
⊙O即为所求.ABCO找一找如图,请找出图中圆的圆心,并写出你找圆心的方法?ABCO 某市要建一个圆形公园,要求公园刚好把动物园A,植物园B和人工湖C包括在内,又要使这个圆形的面积最小,请你给出这个公园的施工图.(A,B,C不在同一直线上)探究活动植物园动物园人工湖 图中工具的CD边所在直线恰好垂直平分AB边,怎样用这个工具找出一个圆的圆心.C数学乐园·圆心练一练1.下列命题不正确的是
A.过一点有无数个圆. B.过两点有无数个圆.
C.弦是圆的一部分. D.过同一直线上三点不能作圆.
2.三角形的外心具有的性质是
A.到三边的距离相等. B.到三个顶点的距离相等.
C.外心在三角形的外. D.外心在三角形内.
3.等腰三角形底边上的高与一腰的垂直平分线的交点是
A.重心 B.垂心 C.外心 D.无法确定.CBC随堂练习4.判断:
(1)经过三点一定可以作圆.( )
(2)三角形的外心就是这个三角形两边垂直平分线的交点.( )
(3)三角形的外心到三边的距离相等.( )
(4)等腰三角形的外心一定在这个三角形内.( )×√××5.在△ABC中,BC=24 cm,外心O到BC的距离为6 cm,求△ABC的外接圆半径 . 【归纳】等边三角形的外接圆的半径等于边长的( )倍.BCA思考:任意四个点是不是可以作一个圆?请举例说明. 不一定1. 四点在一条直线上不能作圆;3. 四点中任意三点不在一条直线可能作圆也可能作不出一个圆.ABCDABCDABCDABCD2. 三点在同一直线上, 另一点不在这条直线上不能作圆;谈收获(1)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.(2)经过一个已知点能作无数个圆!(3)经过两个已知点A,B能作无数个圆!这些圆的圆心在线段AB的垂直平分线上.(4)不在同一直线上的三个点确定一个圆.(5)外接圆,外心的概念.课堂小结谢谢!
