北师大版数学九年级下册3.7 切线长定理 课件(16张ppt)
文档属性
| 名称 | 北师大版数学九年级下册3.7 切线长定理 课件(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览


文档简介
课件16张PPT。第三章
圆7 切线长定理 北师大版数学九年级下册1.经历探究切线长定理的过程,体会应用内切圆相关知识解决问题,渗透转化思想.
2.知道三角形内切圆、内心的概念,理解切线长定理,并会用其解决有关问题.学习目标重点:切线长定理及其应用.
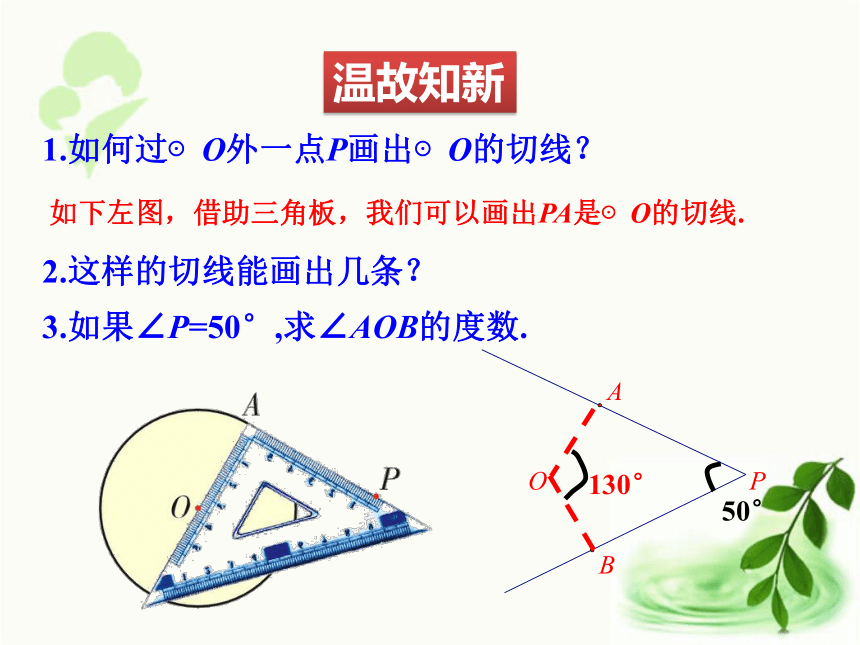
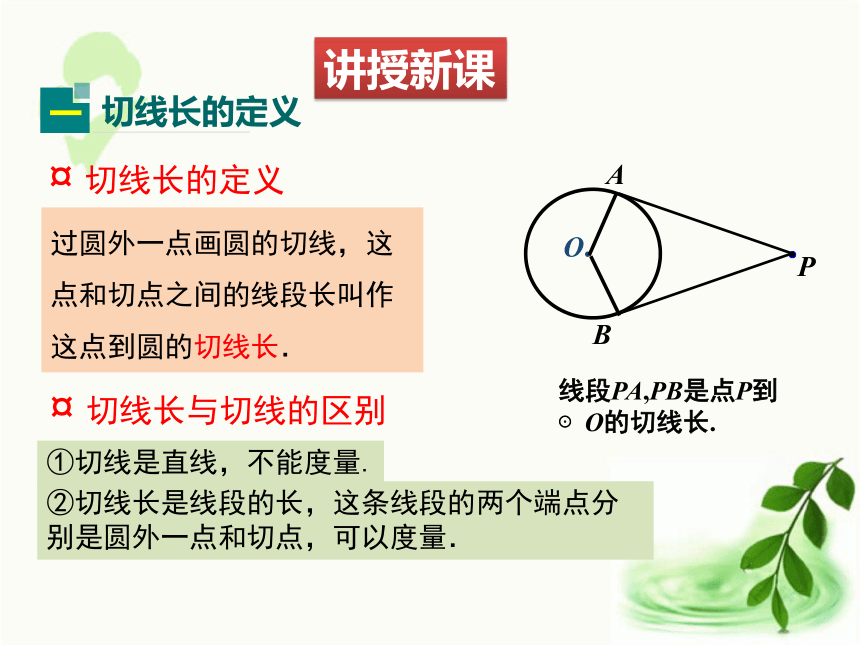
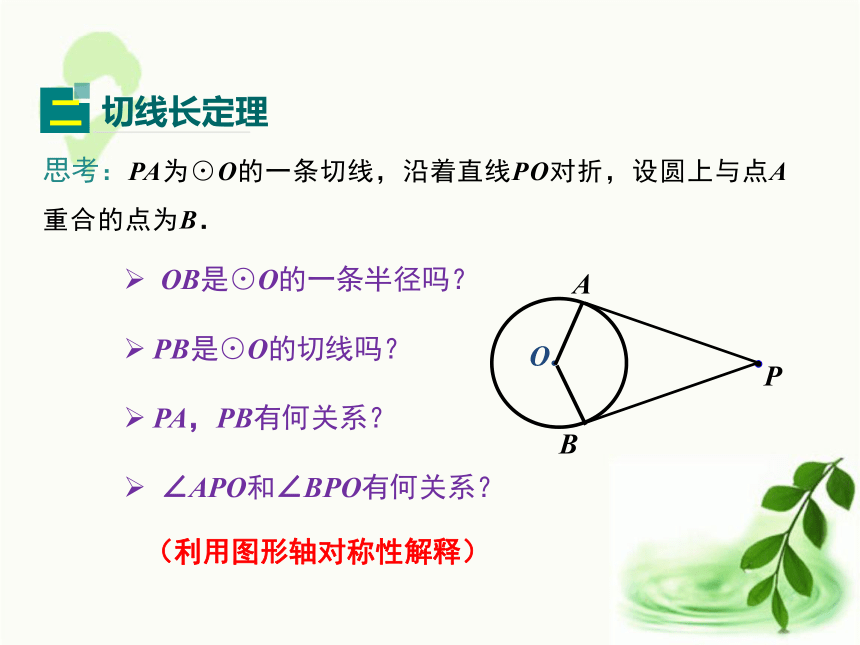
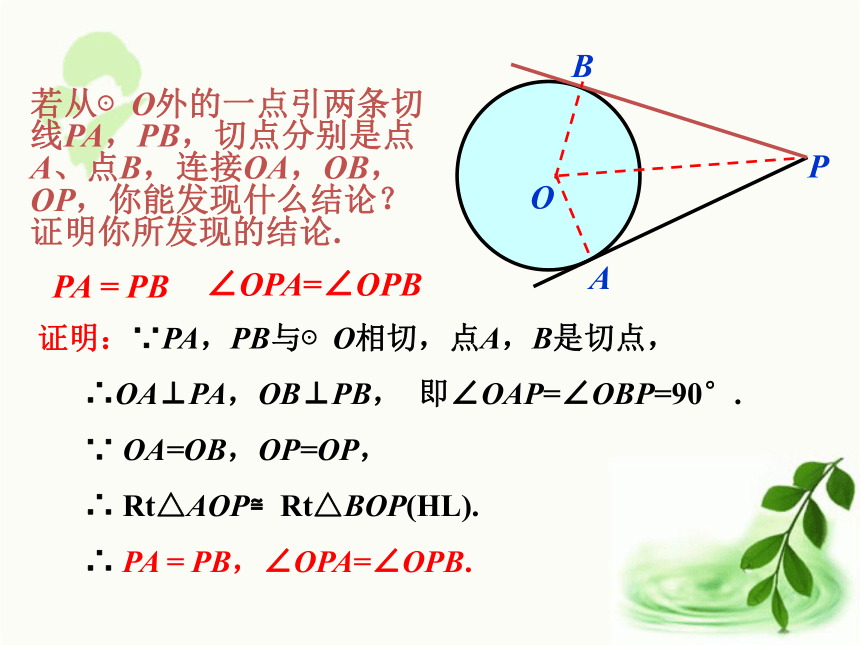
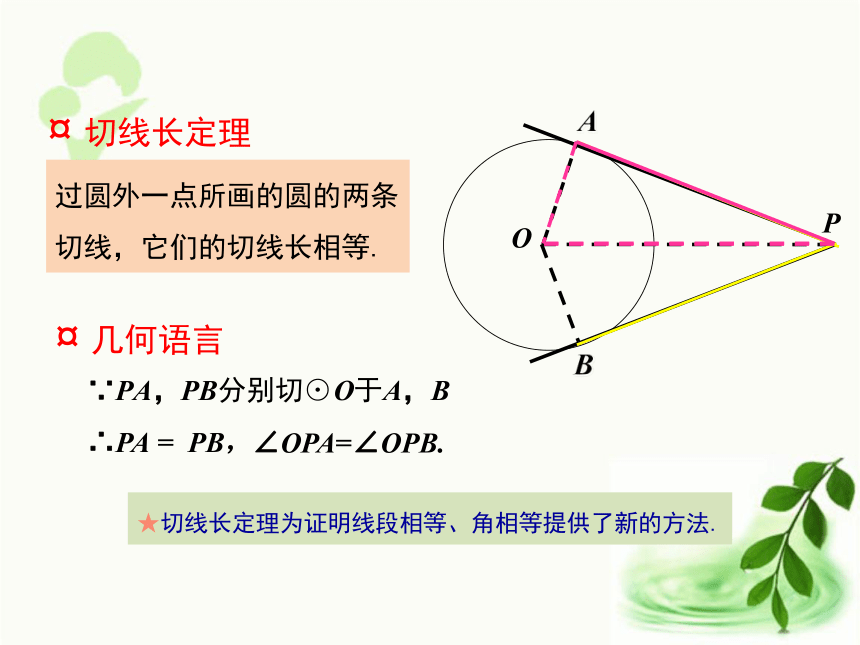
难点:定理的探求、延伸.重点难点1.如何过⊙O外一点P画出⊙O的切线? 2.这样的切线能画出几条?如下左图,借助三角板,我们可以画出PA是⊙O的切线.3.如果∠P=50°,求∠AOB的度数.50°130°O温故知新线段PA,PB是点P到⊙O的切线长.讲授新课过圆外一点画圆的切线,这点和切点之间的线段长叫作这点到圆的切线长.¤ 切线长的定义¤ 切线长与切线的区别①切线是直线,不能度量.②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.思考:PA为⊙O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B. OB是⊙O的一条半径吗? PB是⊙O的切线吗?(利用图形轴对称性解释) PA,PB有何关系? ∠APO和∠BPO有何关系?若从⊙O外的一点引两条切线PA,PB,切点分别是点A、点B,连接OA,OB,OP,你能发现什么结论?证明你所发现的结论.PA = PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB, 即∠OAP=∠OBP=90°.
∵ OA=OB,OP=OP,
∴ Rt△AOP≌Rt△BOP(HL).
∴ PA = PB,∠OPA=∠OPB.BPOA过圆外一点所画的圆的两条切线,它们的切线长相等.∵PA,PB分别切⊙O于A,B∴PA = PB,∠OPA=∠OPB.★切线长定理为证明线段相等、角相等提供了新的方法.¤ 切线长定理¤ 几何语言问题:PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于C.(1)写出图中所有的垂直关系:OA⊥PA,OB ⊥PB,AB ⊥OP.(3)写出图中所有的全等三角形:△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.(4)写出图中所有的等腰三角形:△ABP , AOB.(2)写出图中与∠OAC相等的角:∠OAC=∠OBC=∠APC=∠BPC.练一练:
PA,PB是⊙O的两条切线,A,B是切点,OA=3.(1)若AP=4,则OP= ;(2)若∠BPA=60 °,则OP= .561470°典例精析例2 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=13 cm,BC=14 cm,CA=9 cm,求AF,BD,CE的长.解:设AF=x cm,则AE=x cm.∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).由 BD+CD=BC,可得
(13-x)+(9-x)=14,解得 x=4.∴ AF=4(cm),BD=9(cm),CE=5(cm).想一想:图中你能找出哪些相等的线段?理由是什么?方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.(3)连接圆心和圆外一点.(2)连接两切点;(1)分别连接圆心和切点;。PBAO1.如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果AP=4,∠APB=40°,则∠APO= ,PB= . 20° 4随堂练习2.如图,PA,PB是⊙O的两条切线,切点为A,B,∠P= 50°,点C是⊙O上异于A,B的点,则∠ACB= . 3.△ABC的内切圆⊙O与三边分别切于D,E,F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .65°或115° 30切线长切线长定理作用图形的轴对称性原理提供了证线段和
角相等的新方法辅助线分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.课堂小结谢谢!
圆7 切线长定理 北师大版数学九年级下册1.经历探究切线长定理的过程,体会应用内切圆相关知识解决问题,渗透转化思想.
2.知道三角形内切圆、内心的概念,理解切线长定理,并会用其解决有关问题.学习目标重点:切线长定理及其应用.
难点:定理的探求、延伸.重点难点1.如何过⊙O外一点P画出⊙O的切线? 2.这样的切线能画出几条?如下左图,借助三角板,我们可以画出PA是⊙O的切线.3.如果∠P=50°,求∠AOB的度数.50°130°O温故知新线段PA,PB是点P到⊙O的切线长.讲授新课过圆外一点画圆的切线,这点和切点之间的线段长叫作这点到圆的切线长.¤ 切线长的定义¤ 切线长与切线的区别①切线是直线,不能度量.②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.思考:PA为⊙O的一条切线,沿着直线PO对折,设圆上与点A重合的点为B. OB是⊙O的一条半径吗? PB是⊙O的切线吗?(利用图形轴对称性解释) PA,PB有何关系? ∠APO和∠BPO有何关系?若从⊙O外的一点引两条切线PA,PB,切点分别是点A、点B,连接OA,OB,OP,你能发现什么结论?证明你所发现的结论.PA = PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点,
∴OA⊥PA,OB⊥PB, 即∠OAP=∠OBP=90°.
∵ OA=OB,OP=OP,
∴ Rt△AOP≌Rt△BOP(HL).
∴ PA = PB,∠OPA=∠OPB.BPOA过圆外一点所画的圆的两条切线,它们的切线长相等.∵PA,PB分别切⊙O于A,B∴PA = PB,∠OPA=∠OPB.★切线长定理为证明线段相等、角相等提供了新的方法.¤ 切线长定理¤ 几何语言问题:PA,PB是⊙O的两条切线,A,B为切点,直线OP交⊙O于点D,E,交AB于C.(1)写出图中所有的垂直关系:OA⊥PA,OB ⊥PB,AB ⊥OP.(3)写出图中所有的全等三角形:△AOP≌ △BOP, △AOC≌ △BOC, △ACP≌ △BCP.(4)写出图中所有的等腰三角形:△ABP , AOB.(2)写出图中与∠OAC相等的角:∠OAC=∠OBC=∠APC=∠BPC.练一练:
PA,PB是⊙O的两条切线,A,B是切点,OA=3.(1)若AP=4,则OP= ;(2)若∠BPA=60 °,则OP= .561470°典例精析例2 △ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=13 cm,BC=14 cm,CA=9 cm,求AF,BD,CE的长.解:设AF=x cm,则AE=x cm.∴CE=CD=AC-AE=9-x(cm),
BF=BD=AB-AF=13-x(cm).由 BD+CD=BC,可得
(13-x)+(9-x)=14,解得 x=4.∴ AF=4(cm),BD=9(cm),CE=5(cm).想一想:图中你能找出哪些相等的线段?理由是什么?方法小结:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.(3)连接圆心和圆外一点.(2)连接两切点;(1)分别连接圆心和切点;。PBAO1.如图,PA,PB是⊙O的两条切线,切点分别是A,B,如果AP=4,∠APB=40°,则∠APO= ,PB= . 20° 4随堂练习2.如图,PA,PB是⊙O的两条切线,切点为A,B,∠P= 50°,点C是⊙O上异于A,B的点,则∠ACB= . 3.△ABC的内切圆⊙O与三边分别切于D,E,F三点,如图,已知AF=3,BD+CE=12,则△ABC的周长是 .65°或115° 30切线长切线长定理作用图形的轴对称性原理提供了证线段和
角相等的新方法辅助线分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.课堂小结谢谢!
