湖北省华中师大一附中2020年高二网课课件——双缝实验及光的衍射(20200312)
文档属性
| 名称 | 湖北省华中师大一附中2020年高二网课课件——双缝实验及光的衍射(20200312) |  | |
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-07 10:40:04 | ||
图片预览




文档简介
(共24张PPT)
1
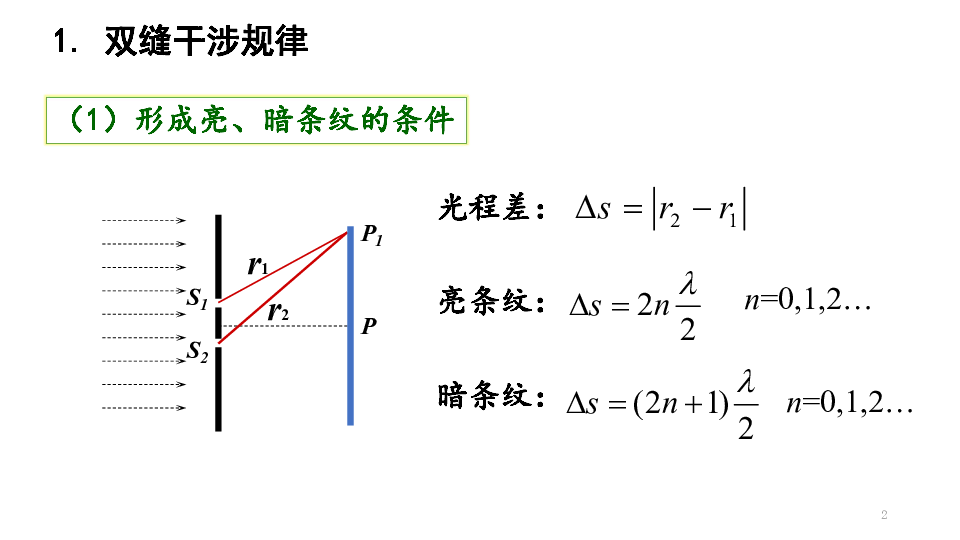
(1)形成亮、暗条纹的条件
光程差:
1. 双缝干涉规律
S1
S2
P1
P
r1
r2
亮条纹:
n=0,1,2…
暗条纹:
n=0,1,2…
2
3
(2)相邻亮(暗)条纹间距大小
相邻亮条纹中心间距
相邻暗条纹中心间距
4
2. 用双缝干涉测量光的波长
(1)实验原理
测出条亮条纹间的距离a,求得相邻两个亮条纹间的距离 。
测出双缝到屏的距离 。
结合双缝之间的间距,由 求波长。
5
(2)实验装置
6
(3)实验步骤
①取下遮光筒左侧的元件,调节光源高度,使光束能直接沿遮光筒轴线把屏照亮;
②按合理顺序在光具座上放置各光学元件,并使各元件的中心位于遮光筒的轴线上;
③用米尺测量双缝到屏(毛玻璃)的距离;
④用测量头(其读数方法同螺旋测微器)测量条亮纹间的距离 a
7
①安装仪器的顺序:光源、凸透镜、滤光片、单缝、双缝、遮光筒、光屏
②双缝与单缝相互平行,且竖直放置
③光源、虑光片、单缝、双缝的中心均在遮光筒的中心轴线上(共光轴)
④若出现在光屏上的光很弱,很有可能是光学器件不共轴所致;若干涉条纹不清晰,与单缝和双缝是否平行有很大关系
(4)注意事项
8
15
20
5
10
0
20
25
15
第1条时读数
第4条时读数
15
20
5
10
0
30
35
40
45
(5)测量头的使用和读数
9
2.192mm,7.869mm,故亮条纹间距为1.65mm
[2015·全国卷Ⅰ] 在双缝干涉实验中,分别用红色和绿色的激光照射同一双缝,在双缝后的屏幕上,红光的干涉条纹间距Δx1与绿光的干涉条纹间距Δx2相比,Δx1________Δx2(填“>”“=”或“<”).若实验中红光的波长为630 nm,双缝到屏幕的距离为1.00 m,测得第1条到第6条亮条纹中心间的距离为10.5 mm,则双缝之间的距离为________mm.
10
11
12
光的衍射:
光能够绕过障碍物偏离直线传播的现象
1. 光的衍射
13
光波发生明显衍射的条件:
障碍物或孔的尺寸比波长小或差不多
日常生活中,障碍物的尺寸比光的波长大很多,故衍射现象不明显。
14
2. 单缝衍射
单缝衍射条纹特点:
(1)明暗相间且不等距条纹
(2)中央亮纹宽而亮
(3)两侧条纹具有对称性,亮纹较窄、较暗
观察屏
衍射条件:单缝足够窄
15
单缝衍射规律:
(1)波长(红光)一定时,单缝窄,其中央条纹宽,各条纹间距大
(2)单缝不变时,光波波长大(红光),其中央亮纹越宽,条纹间隔越大
(3)白光(白炽灯)的单缝衍射,其中央亮条纹为白色,两侧为彩色条纹。
16
3. 圆孔衍射
圆孔
观察屏
光源
(1)圆孔很大——圆形光斑(影的形成)
(2)圆孔比发光光源小——光源的倒立实像(小孔成像)
(3)孔的大小与波长相当——中央亮,周围为明暗相间的同心圆环且亮度小。(光的衍射)
17
在单缝衍射、圆孔衍射的图样中,都有一些亮条纹和暗条纹。
这是由于来自单缝、圆孔不同位置的光,通过缝或孔之后叠加时加强或者削弱的结果。
18
4. 圆盘衍射
光源
圆盘
观察屏
圆盘衍射特点:
(1)阴影外有明暗相间且不等距的同心圆条纹
(2)阴影中心有一亮点,称为“泊松亮斑”
1818年,法国巴黎,鼓励对光的衍射的研究,
菲涅尔按波动说提出了严密解决衍射问题的数学方法;
泊松为了反对光的波动说,利用菲涅尔的数学方法计算圆盘衍射,在一定条件下影的中央会有亮斑;
评委阿拉果实验中观察到该亮斑。
19
5. 其他衍射
各种不同形状的障碍物都能使光发生衍射,致使影的轮廓模糊不清,出现明暗相间的条纹。
20
衍射现象和干涉现象条纹的对比
相同点:由于光的叠加而产生的明暗相间的条纹。
不同点:
①双缝干涉条纹是等间距的,各条纹的亮度差别较小,条纹条数较多。
②单缝衍射条纹不等间距,中央条纹亮而宽,两侧条纹较暗较窄,对称分布。
21
6. 衍射光栅
增加狭缝个数,衍射条纹宽度更窄,亮度更高。
为了得到宽度更窄,亮度更高的光线,由此制成光栅。
22
衍射光栅是由许多等宽的狭缝等距离的排列起来形成的光学仪器。
透射光栅:很平的玻璃上用金刚石刻出一系列等距的平行刻痕,刻痕产生漫反射而不太透光,未刻部分相当于透光狭缝,从而制成透射光栅。
反射光栅:高反射率的金属上刻痕,做成反射光栅。
23
休息10min
24
1
(1)形成亮、暗条纹的条件
光程差:
1. 双缝干涉规律
S1
S2
P1
P
r1
r2
亮条纹:
n=0,1,2…
暗条纹:
n=0,1,2…
2
3
(2)相邻亮(暗)条纹间距大小
相邻亮条纹中心间距
相邻暗条纹中心间距
4
2. 用双缝干涉测量光的波长
(1)实验原理
测出条亮条纹间的距离a,求得相邻两个亮条纹间的距离 。
测出双缝到屏的距离 。
结合双缝之间的间距,由 求波长。
5
(2)实验装置
6
(3)实验步骤
①取下遮光筒左侧的元件,调节光源高度,使光束能直接沿遮光筒轴线把屏照亮;
②按合理顺序在光具座上放置各光学元件,并使各元件的中心位于遮光筒的轴线上;
③用米尺测量双缝到屏(毛玻璃)的距离;
④用测量头(其读数方法同螺旋测微器)测量条亮纹间的距离 a
7
①安装仪器的顺序:光源、凸透镜、滤光片、单缝、双缝、遮光筒、光屏
②双缝与单缝相互平行,且竖直放置
③光源、虑光片、单缝、双缝的中心均在遮光筒的中心轴线上(共光轴)
④若出现在光屏上的光很弱,很有可能是光学器件不共轴所致;若干涉条纹不清晰,与单缝和双缝是否平行有很大关系
(4)注意事项
8
15
20
5
10
0
20
25
15
第1条时读数
第4条时读数
15
20
5
10
0
30
35
40
45
(5)测量头的使用和读数
9
2.192mm,7.869mm,故亮条纹间距为1.65mm
[2015·全国卷Ⅰ] 在双缝干涉实验中,分别用红色和绿色的激光照射同一双缝,在双缝后的屏幕上,红光的干涉条纹间距Δx1与绿光的干涉条纹间距Δx2相比,Δx1________Δx2(填“>”“=”或“<”).若实验中红光的波长为630 nm,双缝到屏幕的距离为1.00 m,测得第1条到第6条亮条纹中心间的距离为10.5 mm,则双缝之间的距离为________mm.
10
11
12
光的衍射:
光能够绕过障碍物偏离直线传播的现象
1. 光的衍射
13
光波发生明显衍射的条件:
障碍物或孔的尺寸比波长小或差不多
日常生活中,障碍物的尺寸比光的波长大很多,故衍射现象不明显。
14
2. 单缝衍射
单缝衍射条纹特点:
(1)明暗相间且不等距条纹
(2)中央亮纹宽而亮
(3)两侧条纹具有对称性,亮纹较窄、较暗
观察屏
衍射条件:单缝足够窄
15
单缝衍射规律:
(1)波长(红光)一定时,单缝窄,其中央条纹宽,各条纹间距大
(2)单缝不变时,光波波长大(红光),其中央亮纹越宽,条纹间隔越大
(3)白光(白炽灯)的单缝衍射,其中央亮条纹为白色,两侧为彩色条纹。
16
3. 圆孔衍射
圆孔
观察屏
光源
(1)圆孔很大——圆形光斑(影的形成)
(2)圆孔比发光光源小——光源的倒立实像(小孔成像)
(3)孔的大小与波长相当——中央亮,周围为明暗相间的同心圆环且亮度小。(光的衍射)
17
在单缝衍射、圆孔衍射的图样中,都有一些亮条纹和暗条纹。
这是由于来自单缝、圆孔不同位置的光,通过缝或孔之后叠加时加强或者削弱的结果。
18
4. 圆盘衍射
光源
圆盘
观察屏
圆盘衍射特点:
(1)阴影外有明暗相间且不等距的同心圆条纹
(2)阴影中心有一亮点,称为“泊松亮斑”
1818年,法国巴黎,鼓励对光的衍射的研究,
菲涅尔按波动说提出了严密解决衍射问题的数学方法;
泊松为了反对光的波动说,利用菲涅尔的数学方法计算圆盘衍射,在一定条件下影的中央会有亮斑;
评委阿拉果实验中观察到该亮斑。
19
5. 其他衍射
各种不同形状的障碍物都能使光发生衍射,致使影的轮廓模糊不清,出现明暗相间的条纹。
20
衍射现象和干涉现象条纹的对比
相同点:由于光的叠加而产生的明暗相间的条纹。
不同点:
①双缝干涉条纹是等间距的,各条纹的亮度差别较小,条纹条数较多。
②单缝衍射条纹不等间距,中央条纹亮而宽,两侧条纹较暗较窄,对称分布。
21
6. 衍射光栅
增加狭缝个数,衍射条纹宽度更窄,亮度更高。
为了得到宽度更窄,亮度更高的光线,由此制成光栅。
22
衍射光栅是由许多等宽的狭缝等距离的排列起来形成的光学仪器。
透射光栅:很平的玻璃上用金刚石刻出一系列等距的平行刻痕,刻痕产生漫反射而不太透光,未刻部分相当于透光狭缝,从而制成透射光栅。
反射光栅:高反射率的金属上刻痕,做成反射光栅。
23
休息10min
24
