六年级下册数学试题-6.2《平面图形的周长与面积》同步练习(有答案) 人教版
文档属性
| 名称 | 六年级下册数学试题-6.2《平面图形的周长与面积》同步练习(有答案) 人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 488.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 17:32:28 | ||
图片预览

文档简介
平面图形的周长与面积
第1关 练速度
1.填空题。
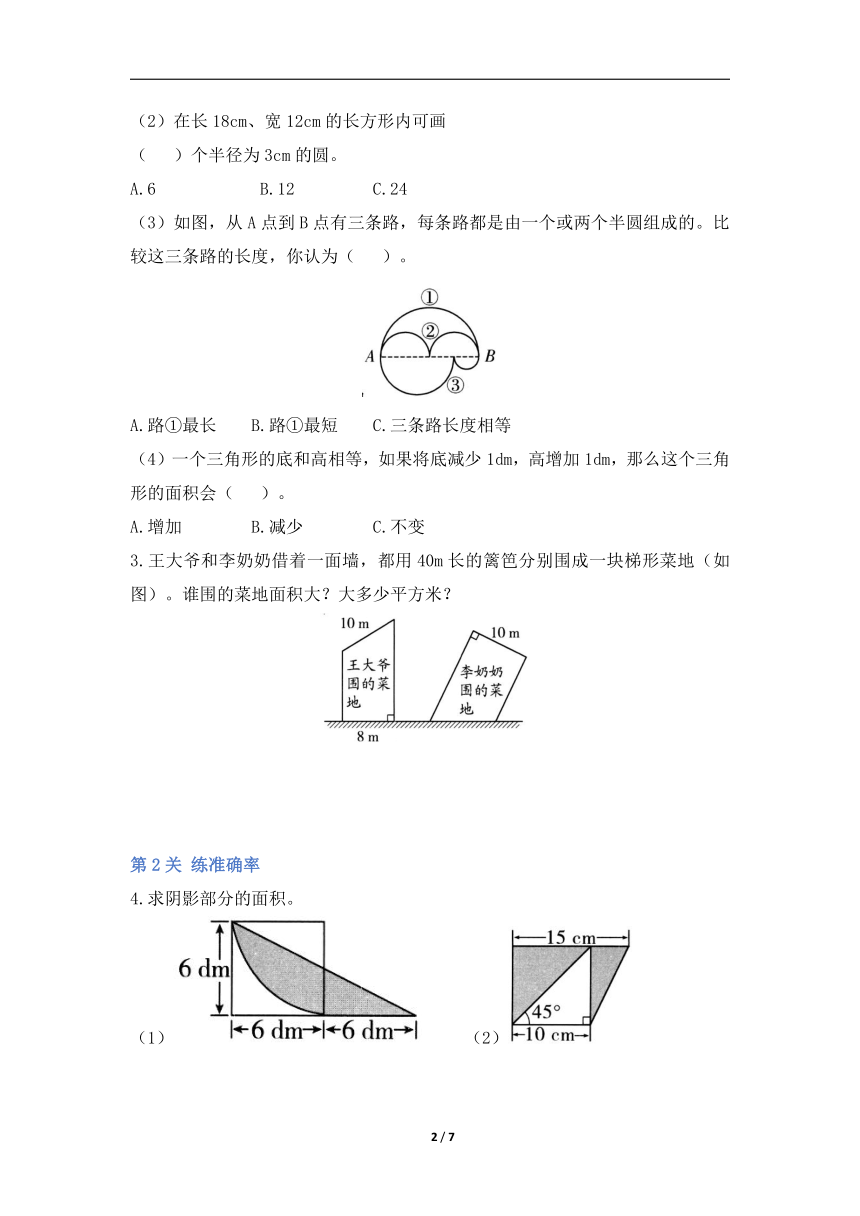
(1)从一块边长10cm的正方形硬纸板上剪下一个最大的圆,这个圆的周长是( )cm,面积是( )cm?。
(2)如图,每个涂色小正方形的面积都是1cm?,那么长方形的面积是( )cm?。
(3)一个圆的半径是4dm,把它的半径增加ldm,周长就增加( )dm,面积就增加( )dm?。
(4)一个平行四边形和一个三角形等底等高,它们的面积和是45m?,则平行四边形的面积是( )m?,三角形的面积是( )m?。
(5)用一个长方形和一个两条直角边分别是3cm、4cm的直角三角形正好拼成了一个直角梯形,这个梯形短的一个底是7cm画图探究一下,它的面积是( )cm?或( )cm。
(6)如图,在半径为10dm的圆内,C为AO的中点,则阴影的面积是( )dm?。
(7)如图,在四边形ABCD中,已知AC与BD互相垂直交于O点,AC的长为5cm,BD的长为12cm,则四边形ABCD的面积是( )cm?。
2.选择题。
(1)一个平行四边形相邻的两条边长分别是10cm和6cm,其中一条边上的高是8cm,这个平行四边形的面积是( )cm?。
A.80 B.60 C.48
(2)在长18cm、宽12cm的长方形内可画
( )个半径为3cm的圆。
A.6 B.12 C.24
(3)如图,从A点到B点有三条路,每条路都是由一个或两个半圆组成的。比较这三条路的长度,你认为( )。
A.路①最长 B.路①最短 C.三条路长度相等
(4)一个三角形的底和高相等,如果将底减少1dm,高增加1dm,那么这个三角形的面积会( )。
A.增加 B.减少 C.不变
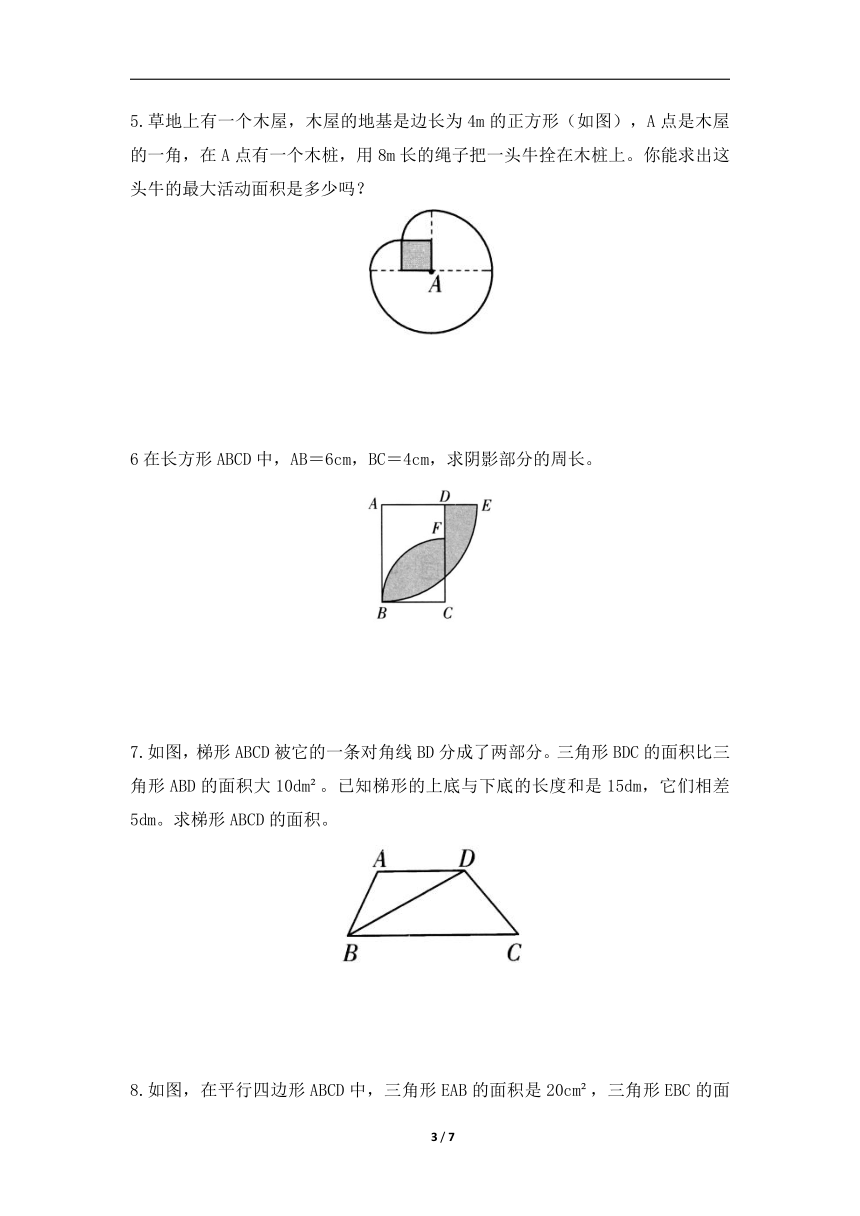
3.王大爷和李奶奶借着一面墙,都用40m长的篱笆分别围成一块梯形菜地(如图)。谁围的菜地面积大?大多少平方米?
第2关 练准确率
4.求阴影部分的面积。
(1) (2)
5.草地上有一个木屋,木屋的地基是边长为4m的正方形(如图),A点是木屋的一角,在A点有一个木桩,用8m长的绳子把一头牛拴在木桩上。你能求出这头牛的最大活动面积是多少吗?
6在长方形ABCD中,AB=6cm,BC=4cm,求阴影部分的周长。
7.如图,梯形ABCD被它的一条对角线BD分成了两部分。三角形BDC的面积比三角形ABD的面积大10dm?。已知梯形的上底与下底的长度和是15dm,它们相差5dm。求梯形ABCD的面积。
8.如图,在平行四边形ABCD中,三角形EAB的面积是20cm?,三角形EBC的面积是8cm?则阴影部分的面积是多少平方厘米?
9.如图所示,在长方形ABCD中,AB=6cm,BC=8cm,阴影部分的面积是15cm?,求四边形EFGH的面积。
第3关 练思维
10.三角形ABC为直角三角形,AB=3cm,BC=4cm,AC=5cm。P为三角形ABC内一点,PE、PF、PD分别垂直于AB、BC、AC,且PE=PF=PD,以P为圆心,PE为半径画一个圆。求圆的面积。
11.如图是一个漂亮而巧妙的图形,图中大圆的直径是10cm,求阴影部分的面积。
12.如图,O1,O2分别是所在圆的圆心。如果两圆半径都是2cm,并且图中两块阴影部分的面积相等,那么EF的长是多少厘米?
参考答案
1.(1)31.4 78.5
(2)54
(3)6.28 28.26
(4)30 15
(5)34 27
(6)53.5
(7)30
2.(1)C(2)A(3)C(4)B
3.(40-10)×8÷2=120(m?) (40-10)×10÷2=150(m?)
150-120=30(m?)
李奶奶围的菜地面积大,大30m?。
4.(1)3.14×6?÷4=28.26(dm?) (2)15×10÷2=75(cm?)
5.3.14×82÷4×3+3.14×4?÷4×2=175.84(m?)
6. ×2×3.14×6+×2×3.14×4+(6-4)×2=19.7(cm)
7.10×2÷5=4(dm) 15×4÷2=30(dm?)
提示:如图,由图知,三角形BDC与三角形ABD等高,所以可由其面积差与上下底之差求得梯形ABCD的高。
8.20-8=12(cm?)
提示:在平行四边形ABCD中,要求阴影部分的面积,只要用三角形EAB的面积减去三角形EBC的面积。
9.15-8×6÷4=3(cm?)
提示:在长方形ABCD中,三角形BAE与三角形CAE同底等高,若从这两个三角形中同时减去三角形AEF,则剩下的图形面积相等。
10.3×4÷2=6(cm?),连接AP、BP、CP,3PE÷2+5PD÷2+4PF÷2=6。而PE=PF=PD,1.5PE+2.5PE+2PE=6,PE=1,圆的面积是3.14×12=3.14(cm?)。
提示:三角形ABC的面积等于 AB×BC÷2,连接AP,BP,CP,而三角形ABC的面积又等于三角形ABP的面积+三角形BCP的面积+三角形ACP的面积,这样可以求出圆的半径,进而求出圆的面积。
11.3.14×(10÷2)?-10×10÷2=28.5(cm?)
提示:如图①,在大圆内画一个最大的正方形,把正方形内的阴影部分平均分成8份,然后把这8个小阴影部分移至正方形外的空白部分(如图②)。要求阴影部分的面积,只需要用大圆的面积减去大正方形的面积即可。
12.3.14×2?÷2=6.28(cm?) 6.28÷2=3.14(cm) 2×2-3.14=0.86(cm)
提示:图中长方形内有两块阴影部分和两块空白部分,由于两块阴影部分的面积相等,两块空白部分的面积也相等,所以长方形的面积相当于是半径为2cm的半圆的面积。先求出长方形的面积,再求出长方形的长,最后用两条半径的长度和减去长方形的长,就是EF的长度。
7 / 7
