苏科版数学八年级下册10.4分式的乘除(1)课件(共30张)
文档属性
| 名称 | 苏科版数学八年级下册10.4分式的乘除(1)课件(共30张) |  | |
| 格式 | zip | ||
| 文件大小 | 49.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 16:08:00 | ||
图片预览








文档简介
(共30张PPT)
10.4 分式的乘除(1)
式 数
类 比
整式 整数
+、-、×、÷、乘方
分式 分数
+、-、
【从单元整体看分式乘除】
类 比
类 比
×、÷、乘方
式与数的运算法则完全一致,
这是数学内部和谐统一的内在需要。
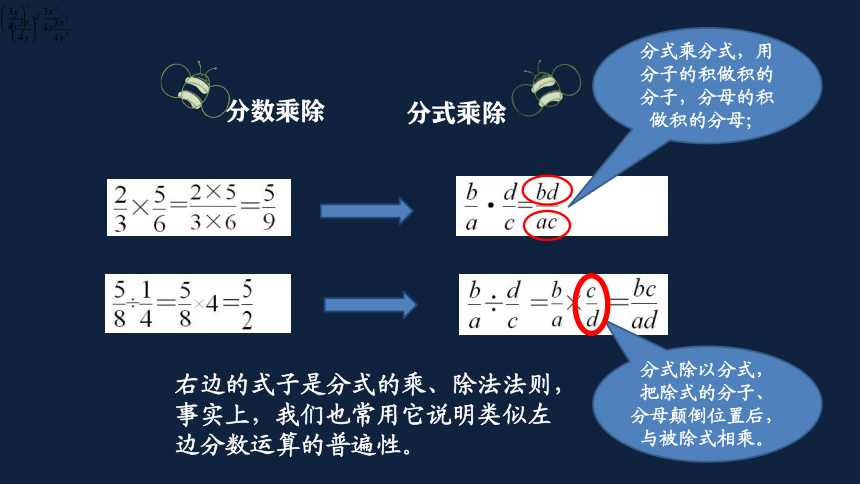
分数乘除
分式乘除
右边的式子是分式的乘、除法法则,事实上,我们也常用它说明类似左边分数运算的普遍性。
分式乘分式,用分子的积做积的分子,分母的积做积的分母;
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
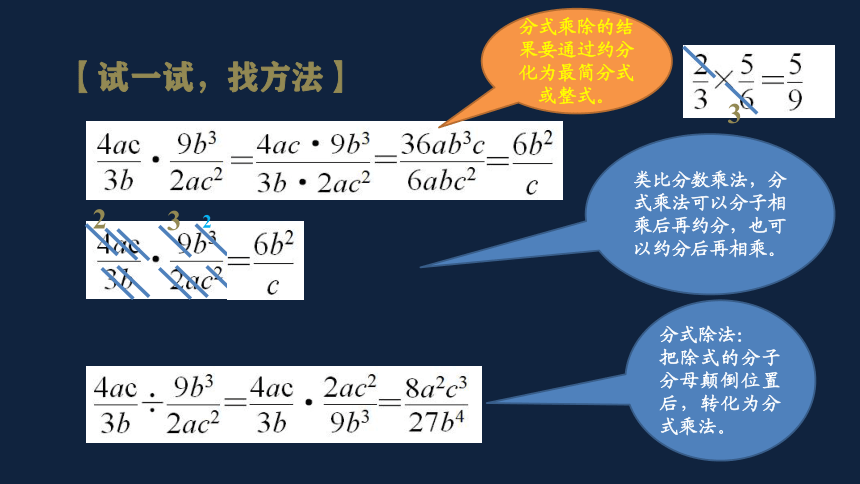
【试一试,找方法】
3
3
2
2
类比分数乘法,分式乘法可以分子相乘后再约分,也可以约分后再相乘。
分式除法:
把除式的分子分母颠倒位置后,转化为分式乘法。
分式乘除的结果要通过约分化为最简分式或整式。
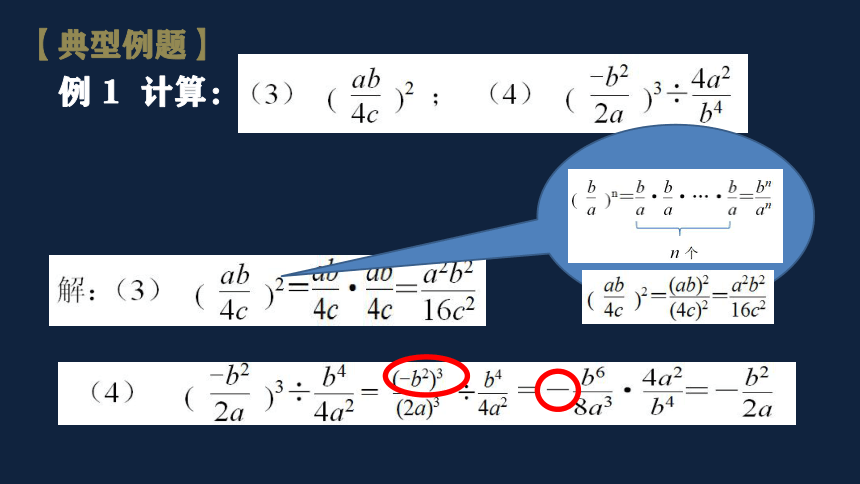
【典型例题】
例 1 计算:
关注:符号,数字因数,字母因式
【典型例题】
例 1 计算:
【解题后反思】
分式乘、除的运算要类比分数乘、除运算来进行;
除法通过颠倒除式分子、分母的位置转化为乘法,
乘方通过乘方的意义转化为乘法。
类比思想与转化思想
【典型例题】
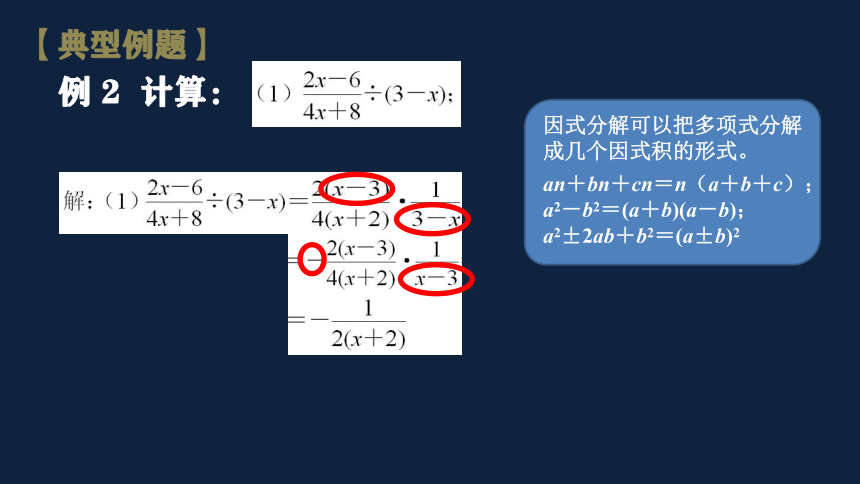
例 2 计算:
因式分解可以把多项式分解成几个因式积的形式。
an+bn+cn=n(a+b+c);
a2-b2=(a+b)(a-b);
a2±2ab+b2=(a±b)2
【典型例题】
例 2 计算:
【小试牛刀】
A
C
④
【小试牛刀】
【小试牛刀】
【融会贯通】
分式乘除的运算法则完全遵循分数乘除的运算法则;
不同之处在于运算时既要关注数字因数的公因数,
又要关注字母因式的公因式。
分子、分母出现多项式时要因式分解,尤其要关注 “符号” 。
分式加减的常用工具是通分,分式乘除的常用工具是约分。
【拓展延伸】
【交流探讨】
如何进行分式的乘、除混合运算?如何进行分式的加、减、乘、除混合运算?
式与数的运算法则、运算顺序完全一致,
这是数式和谐统一的内在需要。
分式 分数
+、-、×、÷、乘方
混合运算的顺序
【交流探讨】
类比
【试一试,找方法】
分式的乘、除混合运算,要按从左到右的顺序进行;
【典型例题】
分式的乘、除混合运算中,符号要格外关注!“定符号,再运算”依然是好的运算程序。
【典型例题】
分式的加、减、乘、除混合运算,先乘除,后加减,如果有括号,先进行括号内的运算。
【典型例题】
【典型例题】
【小试牛刀】
C
A
【小试牛刀】
【小试牛刀】
【拓展延伸】
解法(一)
解法(二)
解法(三)
从部分到整体,体现的是知识和方法的类比与灵活运用,它是数学发展思维的重要方式。
【融会贯通】
分式乘、除混合运算的顺序,分式加、减、乘、除混合运算的顺序都完全遵循数的混合运算顺序;
运算过程中依然要关注符号,尤其是因式为多项式时,“-”的提取要注意式子的整体是否要变号;
整体、代数式的相互替换等思想方法是分式运算中要特别关注的,它往往会令问题的解决有直达本质的豁然开朗。
一种原则,无数内容;
一种方法,到处可用。
——华罗庚
【课后练习】
【课后练习】
同学们,再见!
10.4 分式的乘除(1)
式 数
类 比
整式 整数
+、-、×、÷、乘方
分式 分数
+、-、
【从单元整体看分式乘除】
类 比
类 比
×、÷、乘方
式与数的运算法则完全一致,
这是数学内部和谐统一的内在需要。
分数乘除
分式乘除
右边的式子是分式的乘、除法法则,事实上,我们也常用它说明类似左边分数运算的普遍性。
分式乘分式,用分子的积做积的分子,分母的积做积的分母;
分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
【试一试,找方法】
3
3
2
2
类比分数乘法,分式乘法可以分子相乘后再约分,也可以约分后再相乘。
分式除法:
把除式的分子分母颠倒位置后,转化为分式乘法。
分式乘除的结果要通过约分化为最简分式或整式。
【典型例题】
例 1 计算:
关注:符号,数字因数,字母因式
【典型例题】
例 1 计算:
【解题后反思】
分式乘、除的运算要类比分数乘、除运算来进行;
除法通过颠倒除式分子、分母的位置转化为乘法,
乘方通过乘方的意义转化为乘法。
类比思想与转化思想
【典型例题】
例 2 计算:
因式分解可以把多项式分解成几个因式积的形式。
an+bn+cn=n(a+b+c);
a2-b2=(a+b)(a-b);
a2±2ab+b2=(a±b)2
【典型例题】
例 2 计算:
【小试牛刀】
A
C
④
【小试牛刀】
【小试牛刀】
【融会贯通】
分式乘除的运算法则完全遵循分数乘除的运算法则;
不同之处在于运算时既要关注数字因数的公因数,
又要关注字母因式的公因式。
分子、分母出现多项式时要因式分解,尤其要关注 “符号” 。
分式加减的常用工具是通分,分式乘除的常用工具是约分。
【拓展延伸】
【交流探讨】
如何进行分式的乘、除混合运算?如何进行分式的加、减、乘、除混合运算?
式与数的运算法则、运算顺序完全一致,
这是数式和谐统一的内在需要。
分式 分数
+、-、×、÷、乘方
混合运算的顺序
【交流探讨】
类比
【试一试,找方法】
分式的乘、除混合运算,要按从左到右的顺序进行;
【典型例题】
分式的乘、除混合运算中,符号要格外关注!“定符号,再运算”依然是好的运算程序。
【典型例题】
分式的加、减、乘、除混合运算,先乘除,后加减,如果有括号,先进行括号内的运算。
【典型例题】
【典型例题】
【小试牛刀】
C
A
【小试牛刀】
【小试牛刀】
【拓展延伸】
解法(一)
解法(二)
解法(三)
从部分到整体,体现的是知识和方法的类比与灵活运用,它是数学发展思维的重要方式。
【融会贯通】
分式乘、除混合运算的顺序,分式加、减、乘、除混合运算的顺序都完全遵循数的混合运算顺序;
运算过程中依然要关注符号,尤其是因式为多项式时,“-”的提取要注意式子的整体是否要变号;
整体、代数式的相互替换等思想方法是分式运算中要特别关注的,它往往会令问题的解决有直达本质的豁然开朗。
一种原则,无数内容;
一种方法,到处可用。
——华罗庚
【课后练习】
【课后练习】
同学们,再见!
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
