高中数学人教A版(2019)必修第二册9.1.2分层随机抽样9.1.3获取数据的途径 课件(共32张PPT)
文档属性
| 名称 | 高中数学人教A版(2019)必修第二册9.1.2分层随机抽样9.1.3获取数据的途径 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 10:25:49 | ||
图片预览











文档简介
(共32张PPT)
9.1.2分层随机抽样
1、简单随机抽样的定义;
2、抽签法的一般步骤;
3、随机数法的一般步骤;
4、抽签法与随机数表法的比较;
5、用样本均值估计总体均值
复习回顾
上节课中在对树人中学高一年级学生身高的调查中, 采取简单随机抽样的方式抽取了50名学生。
2.会不会出现样本中 50 个个体大部分来自高个子或矮个子的情形?
3.为什么会出现这种“极端样本”?
1.抽样调查最核心的问题是什么?
4.如何避免这种“极端样本”?
样本代表性
会
抽样的随机性
个体差异较大
分组抽样,减少组内差距
实例引入
思考1:从统计数据来看,哪些因素可能影响高一学生的平均身高?
性别、年龄.
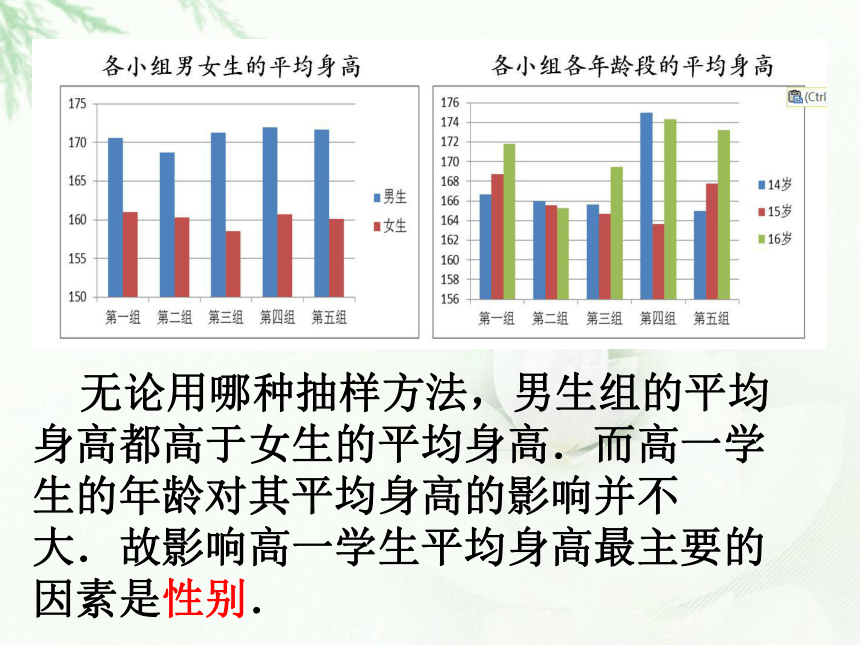
无论用哪种抽样方法,男生组的平均身高都高于女生的平均身高.而高一学生的年龄对其平均身高的影响并不大.故影响高一学生平均身高最主要的因素是性别.
在树人中学高一年级的 712 名学生中, 男生有 326 名、女生有 386 名.
思考2:样本量在男生、女生中应如何分配?
?
?
等额分配
比例分配
要保持样本结构与总体结构的一致性,故应该按比例分配.
在树人中学高一年级的 712 名学生中, 男生有 326 名、女生有 386 名
男生样本量=
女生样本量=
一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.
分层随机抽样的概念
学习新知
每一层抽取的样本数=
总样本量
×
抽样比例
×
该层个体数
=
等可能
说明:1.使用分层随机抽样的前提
分层随机抽样的总体按一个或多个变量划分成若干个子总体(层),并且每一个个体属于且仅属于一个子总体(层),层与层之间差异较大,而层内个体间差异较小.
如果层数分为 2层,第 1 层和第 2 层包含的个体数分别为M 和N 抽取的样本数分别 m 和n
2.使用分层随机抽样应遵循的原则
(1)将相似的个体归入一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则;
(2)分层随机抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比等于抽样比.
总体由差异明显的几个部分组成.
3.适用范围
3.分层随机抽样的实施步骤
(1)分层:按某种特征将总体分成若干层;
(2)按比例确定每层抽取个体的个数;
(3)各层分别按简单随机抽样方法抽取;
(4)综合每层抽样,组成样本.
4.简单随机抽样与分层随机抽样有何异同?
区别:简单随机抽样是从总体中逐个抽取样本;分层随机抽样则首先将总体分成几层,在各层中按比例分配抽取样本.
联系:(1)抽样过程中每个个体被抽到的可能性相等;
(2)每次抽出个体后不再将它放回,即不放回抽样.
典型例题
B
分析抽样方法的确定要依据总体的构成、总体的容量以及样本容量等综合考虑,把握住各种抽样方法的特征是解决此类问题的关键.
例2交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层随机抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101 B.808 C.1 212 D.2 012
B
变:若将“甲社区有驾驶员96人”改为“甲、乙社区驾驶员共99人”,则N的值是什么?
303
练.某高中共有900人,其中高一年级300人,
高二年级200人,高三年级400人,现采用
比例分配的分层随机抽样抽取容量为45的
样本,那么高一、 高二、高三各年级抽取
的人数分别为( )
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20
D
解:各层人数分别为:
学以致用
分层随机抽样的平均数
1.在简单随机抽样中如何估计总体平均数?
2.那么在分层随机抽样中如何估计总体平均数呢?
是否也可以直接用样本平均数进行估计?
学习新知
学习新知
由于用第一层的样本平均数 可以估计第1层的总体平
均数 ,第二层的样本平均数 可以估计第2层的总体平
均数
因此我们可以用
估计总体平均数
对各层样本平均数加权(层权)求和
学习新知
因此,我们可以用样本平均数估计总体平均数
比例分配的随机抽样中
学习新知
在比例分配的分层随机中抽样中
分层随机抽样如何估计总体平均数
学习新知
在树人中学高一年级的 712 名学生,男生有 326 名、女生有 386 名,分别抽取的男生23名男生、27名女生样本数据如下
实例验证
样本女生平均身高=160.6
样本男生平均身高=170.6
163.0 164.0 161.0 157.0 162.0 165.0 168.0 155.0 164.0 162.5
154.0 154.0 164.0 149.0 159.0 161.0 170.0 171.0 155.0 148.0
172.0 162.5 158.0 155.5 157.0 163.0 172.0
例3(2019·全国卷Ⅲ)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 ( )
A.0.5 B.0.6 C.0.7 D.0.8
典型例题
估计效果比较
我们已经学习了两种抽样方法,那么在估计平
均数值的角度,比例分配的分层抽样的估计效
果是否一定比简单随机抽样效果更好呢?
小明用比例分配的分层抽样方法,从高一年级的学
生中抽取了十个样本量为50的样本,计算出样
本平均数。与上一节探究中的相同样本量的简单
随机抽样的结果比较。
1.分层抽样的样本平均的围绕总体平均数波动,
与简单随机抽样的结果相比分层抽样并没有明
显优于简单随机抽样。
2.相对而言,分层抽样的样本平均数波动幅度更均
匀,简单随机抽样的样本平均数有的偏离总体平
均数的幅度比较大的极端数据。
3.分层随机抽样的结果并不是每一次都优于简单
随机抽样。
结 论
课堂总结
1.什么情况下采取分层随机抽样。
2.分层随机抽样的步骤。
3.分层随机抽样中如何用样本估计总体平均值。
1.通过调查获取数据:对于有限总体问题,一般通过抽样调查或普查的方法获取数据.
9.1.3获取数据的途径
2.通过试验获取数据:通过试验获取数据时,我们需要严格控
制试验环境,通过精心的设计安排试验,以提高数据质量,为
获得好的分析结果奠定基础.
3.通过观察获取数据:通过观察自然现象所获取的数据性质比较复杂,其中蕴含着所观察现象的本质信息,这些信息十分宝贵,统计学理论和方法是挖掘这些信息的强有力的工具之一.
4.通过查询获得数据:
我们可以收集前人的劳动成果并加以利用,从而减少收集数据的成本.我们往往把这样获得的数据叫做二手数据.随着信息技术的发展,通过互联网获取数据越来越成为获取二手数据的主要方式.但从网络上查找的数据,因为数据来历和渠道多样,所以质量会参差不齐,必须根据问题背景知识“清洗”数据,去伪存真,为进一步的数据分析奠定基础。
1、必做题:
完成学案导学P107——P111
2、必做题:课时跟踪检测
三十五、三十六选择填空
每日一题
(2019全国卷2文数17).如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥 的体积.
9.1.2分层随机抽样
1、简单随机抽样的定义;
2、抽签法的一般步骤;
3、随机数法的一般步骤;
4、抽签法与随机数表法的比较;
5、用样本均值估计总体均值
复习回顾
上节课中在对树人中学高一年级学生身高的调查中, 采取简单随机抽样的方式抽取了50名学生。
2.会不会出现样本中 50 个个体大部分来自高个子或矮个子的情形?
3.为什么会出现这种“极端样本”?
1.抽样调查最核心的问题是什么?
4.如何避免这种“极端样本”?
样本代表性
会
抽样的随机性
个体差异较大
分组抽样,减少组内差距
实例引入
思考1:从统计数据来看,哪些因素可能影响高一学生的平均身高?
性别、年龄.
无论用哪种抽样方法,男生组的平均身高都高于女生的平均身高.而高一学生的年龄对其平均身高的影响并不大.故影响高一学生平均身高最主要的因素是性别.
在树人中学高一年级的 712 名学生中, 男生有 326 名、女生有 386 名.
思考2:样本量在男生、女生中应如何分配?
?
?
等额分配
比例分配
要保持样本结构与总体结构的一致性,故应该按比例分配.
在树人中学高一年级的 712 名学生中, 男生有 326 名、女生有 386 名
男生样本量=
女生样本量=
一般地,按一个或多个变量把总体划分成若干个子总体,每个个体属于且仅属于一个子总体,在每个子总体中独立地进行简单随机抽样,再把所有子总体中抽取的样本合在一起作为总样本,这样的抽样方法称为分层随机抽样(stratified random sampling),每一个子总体称为层.在分层随机抽样中,如果每层样本量都与层的大小成比例,那么称这种样本量的分配方式为比例分配.
分层随机抽样的概念
学习新知
每一层抽取的样本数=
总样本量
×
抽样比例
×
该层个体数
=
等可能
说明:1.使用分层随机抽样的前提
分层随机抽样的总体按一个或多个变量划分成若干个子总体(层),并且每一个个体属于且仅属于一个子总体(层),层与层之间差异较大,而层内个体间差异较小.
如果层数分为 2层,第 1 层和第 2 层包含的个体数分别为M 和N 抽取的样本数分别 m 和n
2.使用分层随机抽样应遵循的原则
(1)将相似的个体归入一类,即为一层,分层要求每层的各个个体互不交叉,即遵循不重复、不遗漏的原则;
(2)分层随机抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比等于抽样比.
总体由差异明显的几个部分组成.
3.适用范围
3.分层随机抽样的实施步骤
(1)分层:按某种特征将总体分成若干层;
(2)按比例确定每层抽取个体的个数;
(3)各层分别按简单随机抽样方法抽取;
(4)综合每层抽样,组成样本.
4.简单随机抽样与分层随机抽样有何异同?
区别:简单随机抽样是从总体中逐个抽取样本;分层随机抽样则首先将总体分成几层,在各层中按比例分配抽取样本.
联系:(1)抽样过程中每个个体被抽到的可能性相等;
(2)每次抽出个体后不再将它放回,即不放回抽样.
典型例题
B
分析抽样方法的确定要依据总体的构成、总体的容量以及样本容量等综合考虑,把握住各种抽样方法的特征是解决此类问题的关键.
例2交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层随机抽样调查.假设四个社区驾驶员的总人数为N,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数N为( )
A.101 B.808 C.1 212 D.2 012
B
变:若将“甲社区有驾驶员96人”改为“甲、乙社区驾驶员共99人”,则N的值是什么?
303
练.某高中共有900人,其中高一年级300人,
高二年级200人,高三年级400人,现采用
比例分配的分层随机抽样抽取容量为45的
样本,那么高一、 高二、高三各年级抽取
的人数分别为( )
A.15,5,25 B.15,15,15
C.10,5,30 D.15,10,20
D
解:各层人数分别为:
学以致用
分层随机抽样的平均数
1.在简单随机抽样中如何估计总体平均数?
2.那么在分层随机抽样中如何估计总体平均数呢?
是否也可以直接用样本平均数进行估计?
学习新知
学习新知
由于用第一层的样本平均数 可以估计第1层的总体平
均数 ,第二层的样本平均数 可以估计第2层的总体平
均数
因此我们可以用
估计总体平均数
对各层样本平均数加权(层权)求和
学习新知
因此,我们可以用样本平均数估计总体平均数
比例分配的随机抽样中
学习新知
在比例分配的分层随机中抽样中
分层随机抽样如何估计总体平均数
学习新知
在树人中学高一年级的 712 名学生,男生有 326 名、女生有 386 名,分别抽取的男生23名男生、27名女生样本数据如下
实例验证
样本女生平均身高=160.6
样本男生平均身高=170.6
163.0 164.0 161.0 157.0 162.0 165.0 168.0 155.0 164.0 162.5
154.0 154.0 164.0 149.0 159.0 161.0 170.0 171.0 155.0 148.0
172.0 162.5 158.0 155.5 157.0 163.0 172.0
例3(2019·全国卷Ⅲ)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为 ( )
A.0.5 B.0.6 C.0.7 D.0.8
典型例题
估计效果比较
我们已经学习了两种抽样方法,那么在估计平
均数值的角度,比例分配的分层抽样的估计效
果是否一定比简单随机抽样效果更好呢?
小明用比例分配的分层抽样方法,从高一年级的学
生中抽取了十个样本量为50的样本,计算出样
本平均数。与上一节探究中的相同样本量的简单
随机抽样的结果比较。
1.分层抽样的样本平均的围绕总体平均数波动,
与简单随机抽样的结果相比分层抽样并没有明
显优于简单随机抽样。
2.相对而言,分层抽样的样本平均数波动幅度更均
匀,简单随机抽样的样本平均数有的偏离总体平
均数的幅度比较大的极端数据。
3.分层随机抽样的结果并不是每一次都优于简单
随机抽样。
结 论
课堂总结
1.什么情况下采取分层随机抽样。
2.分层随机抽样的步骤。
3.分层随机抽样中如何用样本估计总体平均值。
1.通过调查获取数据:对于有限总体问题,一般通过抽样调查或普查的方法获取数据.
9.1.3获取数据的途径
2.通过试验获取数据:通过试验获取数据时,我们需要严格控
制试验环境,通过精心的设计安排试验,以提高数据质量,为
获得好的分析结果奠定基础.
3.通过观察获取数据:通过观察自然现象所获取的数据性质比较复杂,其中蕴含着所观察现象的本质信息,这些信息十分宝贵,统计学理论和方法是挖掘这些信息的强有力的工具之一.
4.通过查询获得数据:
我们可以收集前人的劳动成果并加以利用,从而减少收集数据的成本.我们往往把这样获得的数据叫做二手数据.随着信息技术的发展,通过互联网获取数据越来越成为获取二手数据的主要方式.但从网络上查找的数据,因为数据来历和渠道多样,所以质量会参差不齐,必须根据问题背景知识“清洗”数据,去伪存真,为进一步的数据分析奠定基础。
1、必做题:
完成学案导学P107——P111
2、必做题:课时跟踪检测
三十五、三十六选择填空
每日一题
(2019全国卷2文数17).如图,长方体ABCD–A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.
(1)证明:BE⊥平面EB1C1;
(2)若AE=A1E,AB=3,求四棱锥 的体积.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
