人教A版(2019)高中数学必修第二册教学课件:8.1 基本立体图形 (共29张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册教学课件:8.1 基本立体图形 (共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 10:27:11 | ||
图片预览


文档简介
(共29张PPT)
8.1 基本立体图形(1)多面体
一、生活中的立体图形
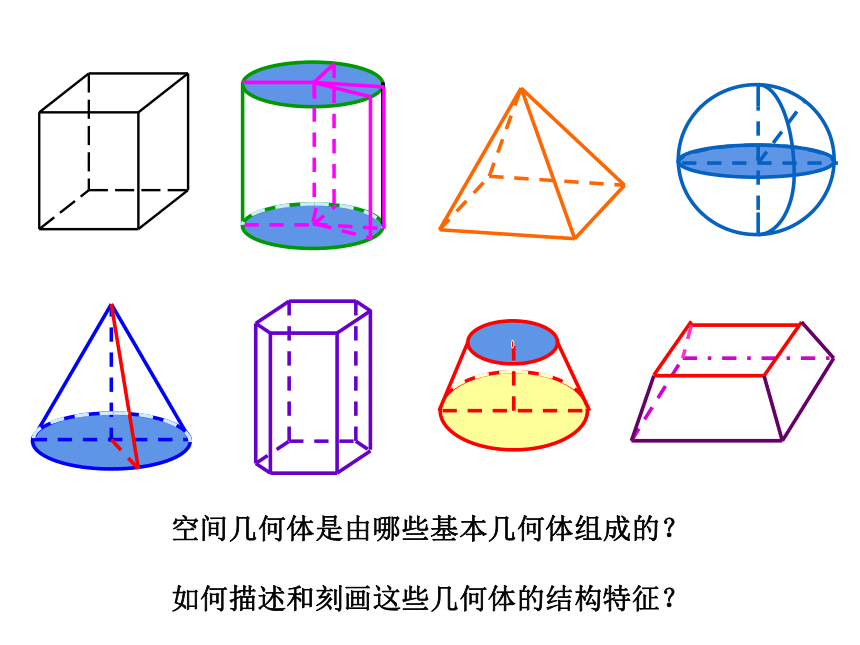
空间几何体是由哪些基本几何体组成的?
如何描述和刻画这些几何体的结构特征?
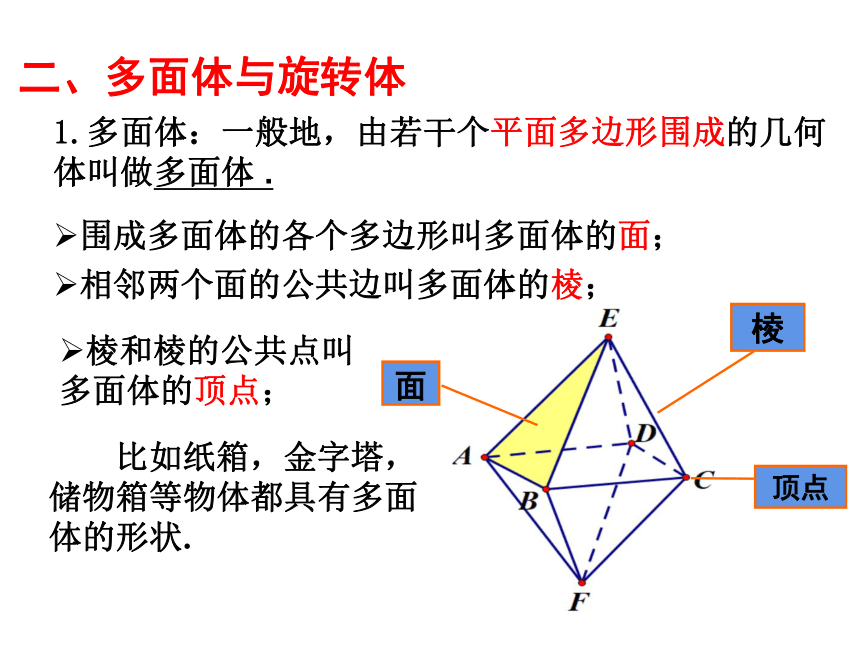
1.多面体:一般地,由若干个平面多边形围成的几何 体叫做多面体 .
二、多面体与旋转体
围成多面体的各个多边形叫多面体的面;
棱
面
顶点
相邻两个面的公共边叫多面体的棱;
棱和棱的公共点叫多面体的顶点;
比如纸箱,金字塔,储物箱等物体都具有多面体的形状.
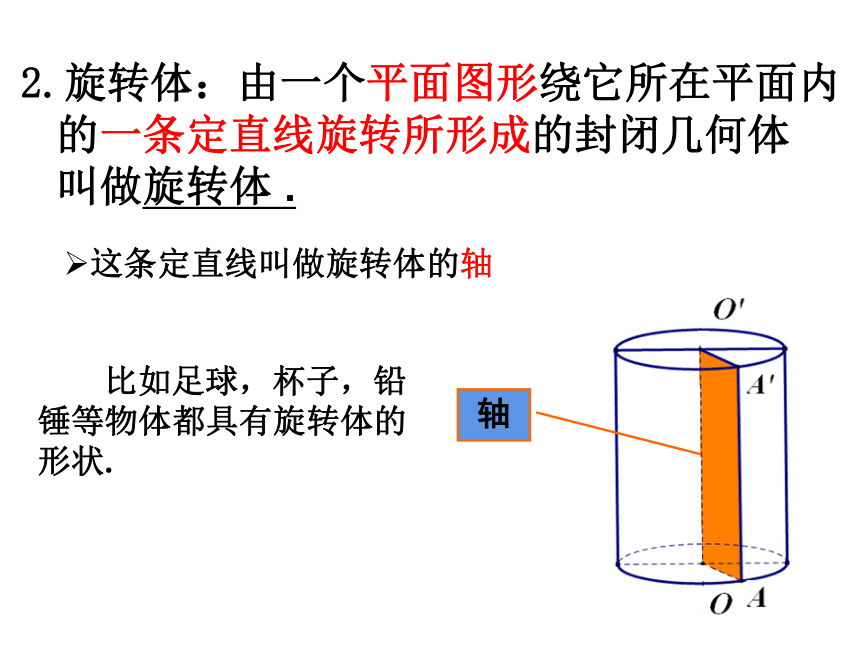
2.旋转体:由一个平面图形绕它所在平面内
的一条定直线旋转所形成的封闭几何体
叫做旋转体 .
这条定直线叫做旋转体的轴
轴
比如足球,杯子,铅锤等物体都具有旋转体的形状.
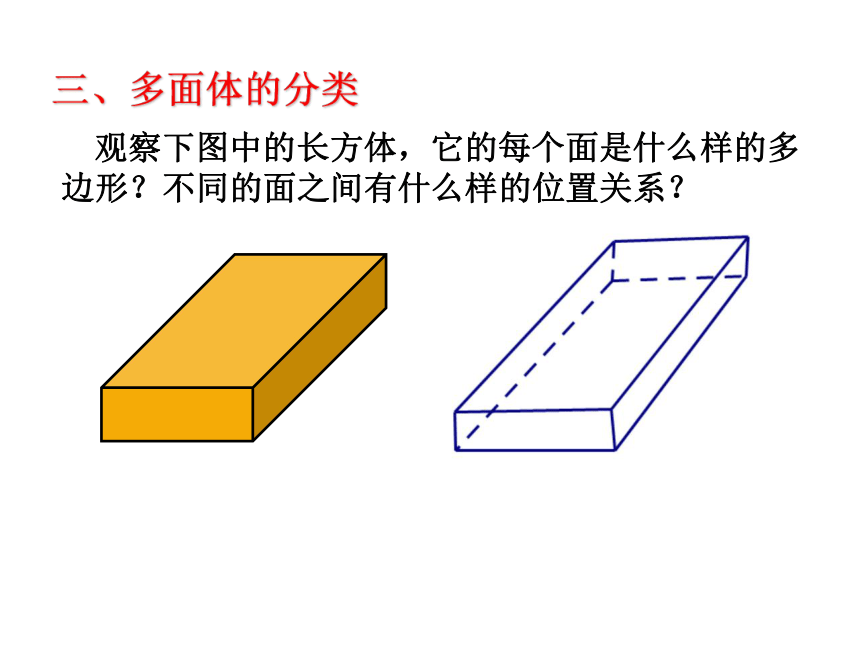
三、多面体的分类
观察下图中的长方体,它的每个面是什么样的多边形?不同的面之间有什么样的位置关系?
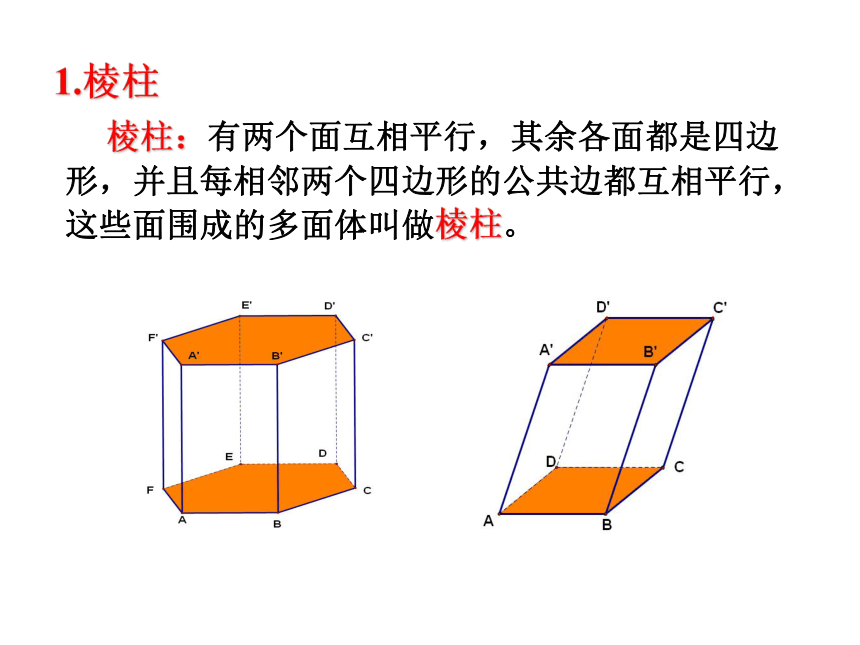
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的多面体叫做棱柱。
1.棱柱
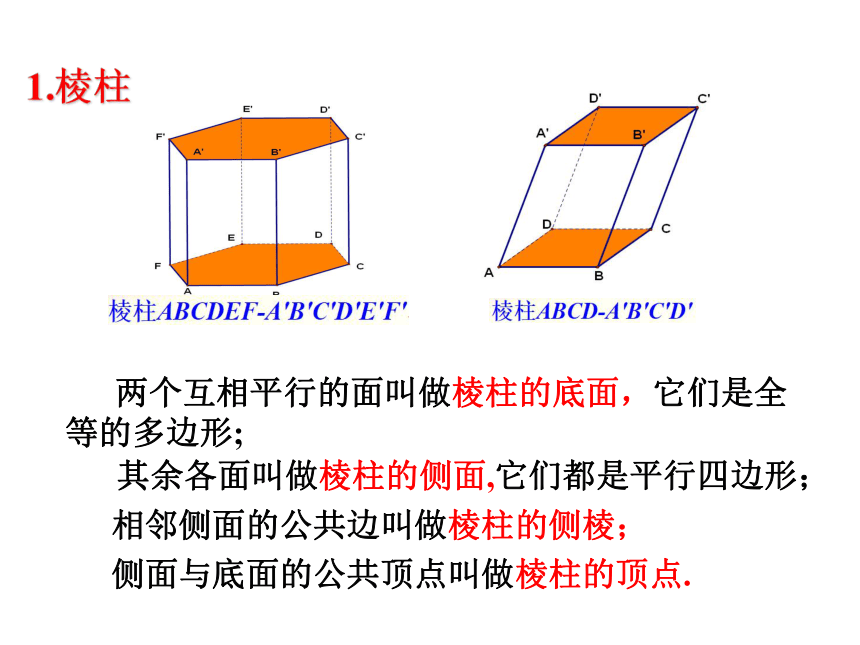
1.棱柱
两个互相平行的面叫做棱柱的底面,它们是全等的多边形;
其余各面叫做棱柱的侧面,它们都是平行四边形;
相邻侧面的公共边叫做棱柱的侧棱;
侧面与底面的公共顶点叫做棱柱的顶点.
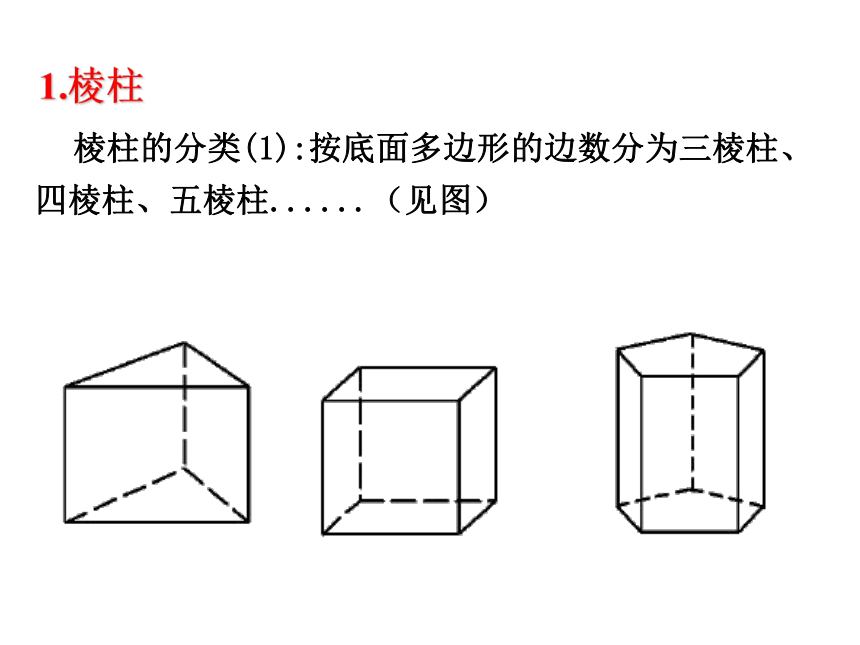
棱柱的分类(1):按底面多边形的边数分为三棱柱、四棱柱、五棱柱......(见图)
1.棱柱
棱柱的分类(2):按侧棱与底面的关系分类:侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱.
1.棱柱
底面是平行四边形的棱柱叫做平行六面体.
底面是正多边形的直棱柱叫做正棱柱.
你能举出生活中哪些物体所对应的几何体是棱柱吗
2.棱锥
一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
2.棱锥
棱锥S-ABCDE
这个多边形面叫做棱锥的底面.
有公共顶点的各个三角形面叫做棱锥的侧面.
相邻侧面的公共边叫做棱锥的侧棱.
各侧面的公共顶点叫做棱锥的顶点.
三棱锥
四棱锥
五棱锥
(四面体)
2.棱锥
棱锥的分类(1):按照底面多边形的边数分为:三棱锥、四棱锥、五棱锥......
四面体是最简单的空间几何体之一,它有什么特点?
1.有四个面,每个面都是三角形.
2.每个三角形的顶点都可以作为三棱锥的顶点.
3.每个面都可以作为三棱锥的底面.
正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.
O
S
A
B
C
D
E
正棱锥的基本性质
各侧棱相等,各侧面 是全等的等腰三角形,各等腰 三角形底边上的高相等.
M
2.棱锥
你能举出生活中哪些物体所对应的几何体是棱锥吗
小试身手
1.判断
(1)长方体是四棱柱,直四棱柱都是长方体.( )
(2)四棱柱、五棱锥都是六面体. ( )
2.填空
(1)一个几何体由7个面围成,其中两个面是互相平行且相等的五边形,其他各面都是全等的矩形,则这个几何体是_______.
(2)一个多面体最少有____个面,此时这个多面体是
_______.
×
√
五棱柱
四
三棱锥
(四面体)
3.下列几何体中为棱柱的是________________.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(1) (3) (5)
3.棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台.
下底面
上底面
侧面
侧棱
顶点
你能仿照棱锥中侧面、侧棱、顶点的定义,写出棱台的侧面、侧棱、顶点吗?
A
B
C
D
E
F
棱台ABC-DEF
用正棱锥截得的棱台叫作正棱台.
正棱台性质:
正棱台的侧面是全等的等腰梯形,
正棱锥
正四棱台
3.棱台
你能举出生活中哪些物体所对应的几何体是棱台吗
4.判断下列几何体是不是棱台,为什么?
小试身手
不是
不是
是
小试身手
5.判断
(1)一个棱柱至少有5个面. ( )
(2)平行六面体中相对的两个面是全等的平行四边形.( )
(3)有一个面是平行四边形的棱锥一定是四棱锥. ( )
(4)正棱锥的侧面是全等的等腰三角形. ( )
√
√
√
√
小试身手
6.如图,长方体ABCD-A'B'C'D'被一个平面截成两个几何体,其中EH∥B'C'∥FG,请说出这两个几何体的名称.
解:两个几何体均为棱柱.
分别为:棱柱HC'G-EB'F
和棱柱D'HGCD-A'EFBA.
四、典例分析
例1 你能分清楚下列几何体之间的关系吗?
多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体
试着用Venn图表示出来.
解:如图所示
拓广探索
下列命题是否正确,若正确请说明理由,若不正确请举出反例.
1.有两个面平行,其他各面都是平行四边形的多面体是棱柱 .
( )
×
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的多面体叫做棱柱
反例:
拓广探索
2.有两个面平行且相似,其他各个面都是梯形的多面体是棱台 ( )
×
反例:
五、课堂小结
1.精读课本96-101页.
2.完成导学导练.
六、作业
8.1 基本立体图形(1)多面体
一、生活中的立体图形
空间几何体是由哪些基本几何体组成的?
如何描述和刻画这些几何体的结构特征?
1.多面体:一般地,由若干个平面多边形围成的几何 体叫做多面体 .
二、多面体与旋转体
围成多面体的各个多边形叫多面体的面;
棱
面
顶点
相邻两个面的公共边叫多面体的棱;
棱和棱的公共点叫多面体的顶点;
比如纸箱,金字塔,储物箱等物体都具有多面体的形状.
2.旋转体:由一个平面图形绕它所在平面内
的一条定直线旋转所形成的封闭几何体
叫做旋转体 .
这条定直线叫做旋转体的轴
轴
比如足球,杯子,铅锤等物体都具有旋转体的形状.
三、多面体的分类
观察下图中的长方体,它的每个面是什么样的多边形?不同的面之间有什么样的位置关系?
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的多面体叫做棱柱。
1.棱柱
1.棱柱
两个互相平行的面叫做棱柱的底面,它们是全等的多边形;
其余各面叫做棱柱的侧面,它们都是平行四边形;
相邻侧面的公共边叫做棱柱的侧棱;
侧面与底面的公共顶点叫做棱柱的顶点.
棱柱的分类(1):按底面多边形的边数分为三棱柱、四棱柱、五棱柱......(见图)
1.棱柱
棱柱的分类(2):按侧棱与底面的关系分类:侧棱与底面不垂直的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱.
1.棱柱
底面是平行四边形的棱柱叫做平行六面体.
底面是正多边形的直棱柱叫做正棱柱.
你能举出生活中哪些物体所对应的几何体是棱柱吗
2.棱锥
一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.
棱锥的底面
棱锥的侧面
棱锥的顶点
棱锥的侧棱
S
A
B
C
D
E
2.棱锥
棱锥S-ABCDE
这个多边形面叫做棱锥的底面.
有公共顶点的各个三角形面叫做棱锥的侧面.
相邻侧面的公共边叫做棱锥的侧棱.
各侧面的公共顶点叫做棱锥的顶点.
三棱锥
四棱锥
五棱锥
(四面体)
2.棱锥
棱锥的分类(1):按照底面多边形的边数分为:三棱锥、四棱锥、五棱锥......
四面体是最简单的空间几何体之一,它有什么特点?
1.有四个面,每个面都是三角形.
2.每个三角形的顶点都可以作为三棱锥的顶点.
3.每个面都可以作为三棱锥的底面.
正棱锥
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.
O
S
A
B
C
D
E
正棱锥的基本性质
各侧棱相等,各侧面 是全等的等腰三角形,各等腰 三角形底边上的高相等.
M
2.棱锥
你能举出生活中哪些物体所对应的几何体是棱锥吗
小试身手
1.判断
(1)长方体是四棱柱,直四棱柱都是长方体.( )
(2)四棱柱、五棱锥都是六面体. ( )
2.填空
(1)一个几何体由7个面围成,其中两个面是互相平行且相等的五边形,其他各面都是全等的矩形,则这个几何体是_______.
(2)一个多面体最少有____个面,此时这个多面体是
_______.
×
√
五棱柱
四
三棱锥
(四面体)
3.下列几何体中为棱柱的是________________.
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(1) (3) (5)
3.棱台
用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台.
下底面
上底面
侧面
侧棱
顶点
你能仿照棱锥中侧面、侧棱、顶点的定义,写出棱台的侧面、侧棱、顶点吗?
A
B
C
D
E
F
棱台ABC-DEF
用正棱锥截得的棱台叫作正棱台.
正棱台性质:
正棱台的侧面是全等的等腰梯形,
正棱锥
正四棱台
3.棱台
你能举出生活中哪些物体所对应的几何体是棱台吗
4.判断下列几何体是不是棱台,为什么?
小试身手
不是
不是
是
小试身手
5.判断
(1)一个棱柱至少有5个面. ( )
(2)平行六面体中相对的两个面是全等的平行四边形.( )
(3)有一个面是平行四边形的棱锥一定是四棱锥. ( )
(4)正棱锥的侧面是全等的等腰三角形. ( )
√
√
√
√
小试身手
6.如图,长方体ABCD-A'B'C'D'被一个平面截成两个几何体,其中EH∥B'C'∥FG,请说出这两个几何体的名称.
解:两个几何体均为棱柱.
分别为:棱柱HC'G-EB'F
和棱柱D'HGCD-A'EFBA.
四、典例分析
例1 你能分清楚下列几何体之间的关系吗?
多面体,长方体,棱柱,棱锥,棱台,直棱柱,四面体,平行六面体
试着用Venn图表示出来.
解:如图所示
拓广探索
下列命题是否正确,若正确请说明理由,若不正确请举出反例.
1.有两个面平行,其他各面都是平行四边形的多面体是棱柱 .
( )
×
棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的多面体叫做棱柱
反例:
拓广探索
2.有两个面平行且相似,其他各个面都是梯形的多面体是棱台 ( )
×
反例:
五、课堂小结
1.精读课本96-101页.
2.完成导学导练.
六、作业
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
