湖北省华中师大一附中2020年网课课件——单摆(20200222)
文档属性
| 名称 | 湖北省华中师大一附中2020年网课课件——单摆(20200222) |

|
|
| 格式 | zip | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
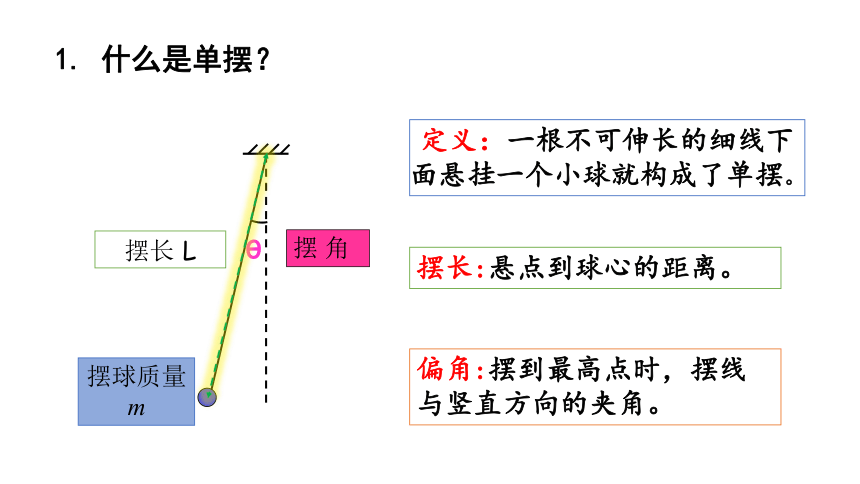
1. 什么是单摆?
摆长 L
摆 角
θ
摆长:悬点到球心的距离。
定义:一根不可伸长的细线下面悬挂一个小球就构成了单摆。
偏角:摆到最高点时,摆线与竖直方向的夹角。
摆球质量m
理想化条件:
单摆是实际摆的理想化模型。
摆线不可伸长
摆线可视为轻绳
摆球可视为质点
空气阻力忽略不计
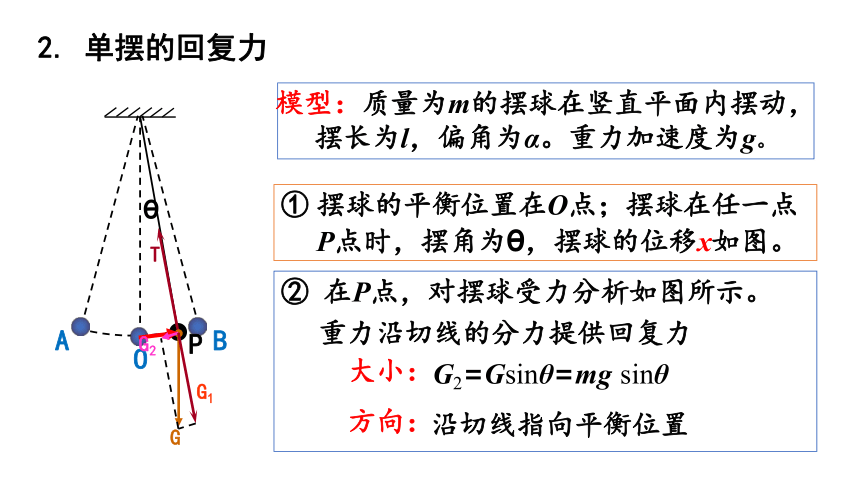
② 在P点,对摆球受力分析如图所示。
B
A
O
2. 单摆的回复力
摆球的平衡位置在O点;摆球在任一点P点时,摆角为θ,摆球的位移x如图。
大小:
G2=Gsinθ=mg sinθ
方向:
沿切线指向平衡位置
模型:质量为m的摆球在竖直平面内摆动,摆长为l,偏角为α。重力加速度为g。
P
θ
T
G
G2
G1
重力沿切线的分力提供回复力
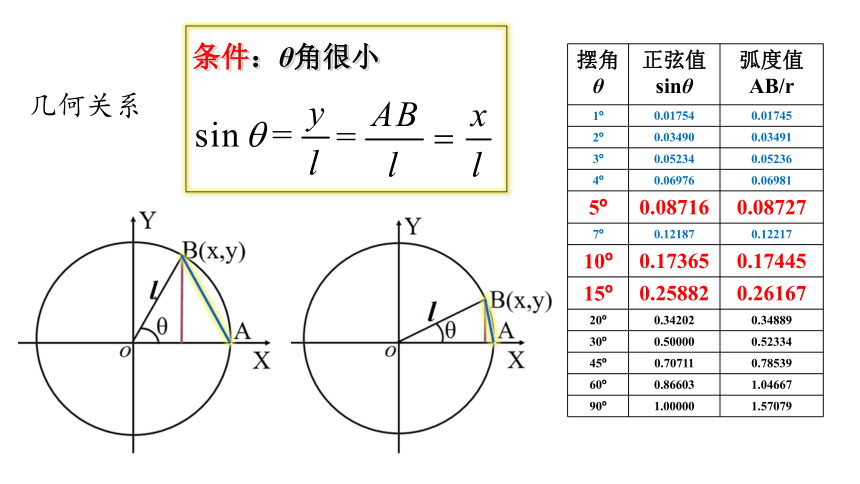
几何关系
摆角
θ 正弦值
sinθ 弧度值
AB/r
1? 0.01754 0.01745
2? 0.03490 0.03491
3? 0.05234 0.05236
4? 0.06976 0.06981
5? 0.08716 0.08727
7? 0.12187 0.12217
10? 0.17365 0.17445
15? 0.25882 0.26167
20? 0.34202 0.34889
30? 0.50000 0.52334
45? 0.70711 0.78539
60? 0.86603 1.04667
90? 1.00000 1.57079
条件:θ角很小
B
A
O
P
θ
T
G
G2
G1
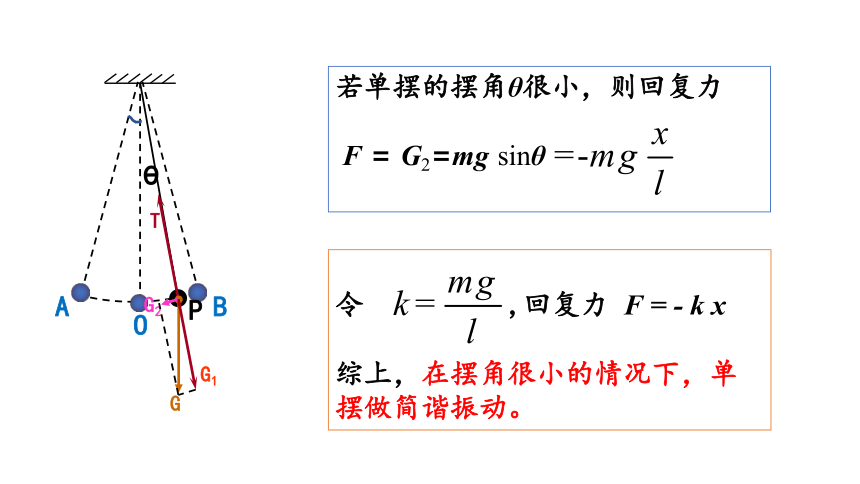
若单摆的摆角θ很小,则回复力
F = G2=mg sinθ
令 ,回复力 F = - k x
综上,在摆角很小的情况下,单摆做简谐振动。
思考: (多选)
下列有关单摆运动过程中的受力,说法正确的是( )
A.单摆运动的回复力是重力和摆线拉力的合力
B.单摆运动的回复力是重力沿圆弧切线方向的一个分力
C.单摆运动的回复力是摆线拉力的一个分力
D.单摆经过平衡位置时合力为零
E. 摆球在运动过程中仅受到重力和绳子的拉力
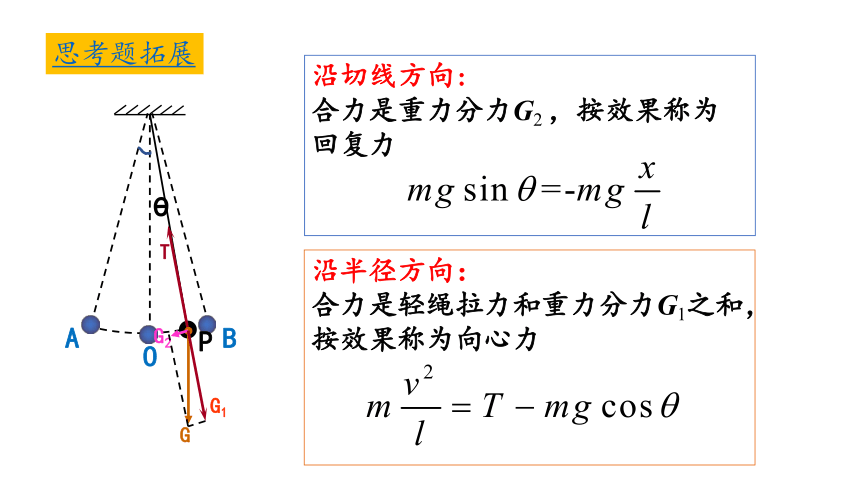
沿切线方向:
合力是重力分力G2 ,按效果称为回复力
沿半径方向:
合力是轻绳拉力和重力分力G1之和,按效果称为向心力
思考题拓展
B
A
O
P
θ
T
G
G2
G1
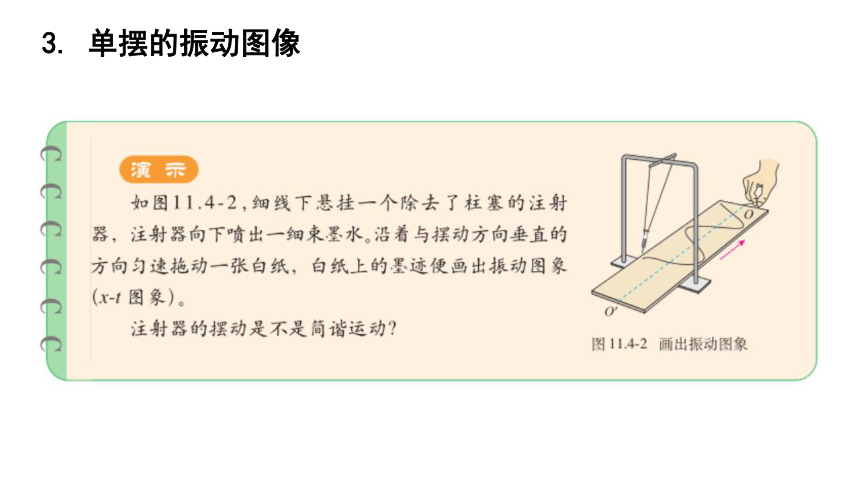
3. 单摆的振动图像
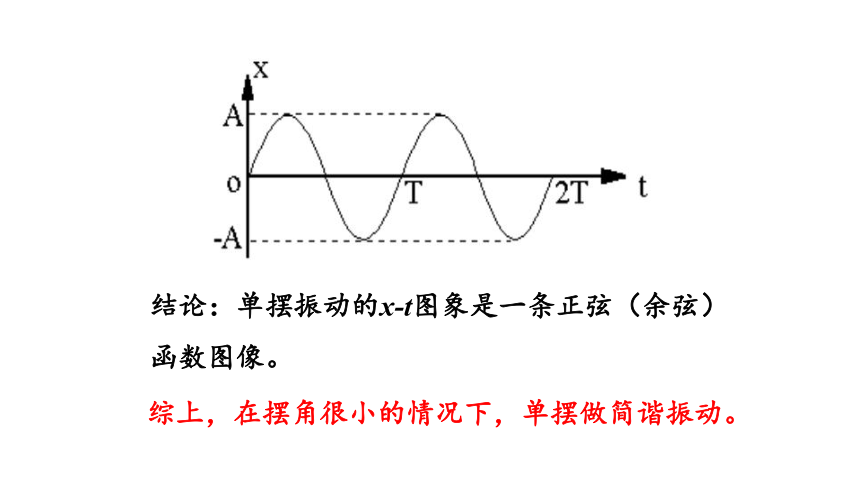
综上,在摆角很小的情况下,单摆做简谐振动。
结论:单摆振动的x-t图象是一条正弦(余弦)函数图像。
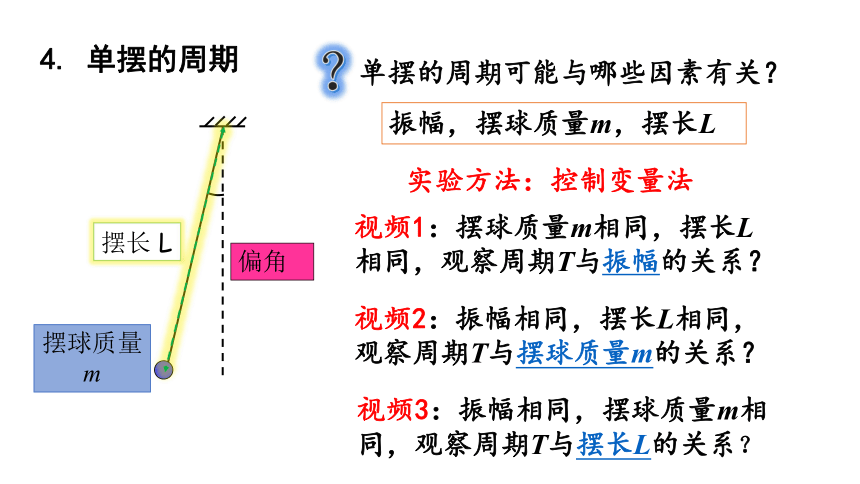
4. 单摆的周期
摆球质量m
偏角
摆长 L
单摆的周期可能与哪些因素有关?
?
实验方法:控制变量法
视频1:摆球质量m相同,摆长L相同,观察周期T与振幅的关系?
视频2:振幅相同,摆长L相同,观察周期T与摆球质量m的关系?
视频3:振幅相同,摆球质量m相同,观察周期T与摆长L的关系?
振幅,摆球质量m,摆长L
实验结论:在同一个地点,单摆周期与摆球质量和振幅无关,仅与摆长有关系,且单摆周期与摆长的平方根成正比。
荷兰物理学家惠更斯(1629---1695)通过实验进一步找到:
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
实验表明单摆周期与单摆所在处的重力加速度有关。 g越小,T越大。
O
弹簧振子
单摆
回复力
周期
对所有简谐振动都成立
(1)计时器:利用等时性
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)。
周期T =2s的单摆叫做秒摆
(2)测定当地的重力加速度
5. 单摆周期的应用
测出单摆的摆长和周期就可求重力加速度
实验:用单摆测定重力加速度
①制作单摆,并确保其做简谐振动
选材:金属小球 、细线(长1 m左右)
操作:固定悬点,单摆从平衡位置拉开一个较小的角度,无初速度释放小球。
②测摆长
刻度尺测摆线长L0
游标卡尺测小球直径d
③测周期
累计法测周期
摆长 L=L0+d/2
④数据处理
方案1:平均值法
方案2:图像法
课堂小结:
一、单摆概念
二、回复力
四、周期
三、图像: 正弦或余弦曲线
① 线的伸缩和质量不计
②小球可看作质点(摆长为悬点到球心的距离)
① F = mg sinθ
② θ 很小时,F=-k x (简谐运动的条件)
五、周期的应用:
实验:用单摆测定重力加速度
钟摆
若单摆的摆长不变,摆球的质量增加为原来的4倍,摆球经过平衡位置的速度变为原来的1/2,则单摆振动的( )
A.频率不变,振幅不变
B.周期不变,振幅改变
C.频率改变,振幅改变
D.周期改变,振幅不变
练习 1
球A在光滑圆弧凹槽的右端,球B在圆弧的圆心。圆弧的半径远大于弧长,且A、B小球可视为质点。A、B同时无初速释放,下列说法正确的是( )
球A先到达O点
球B先到达O点
球A、B同时先到达O点
无法判断
θ
A
练习 2
B
O
练习 3
一小球挂于O点,细线长为l,O点正下方 l /2处有一铁钉。将小球拉至A处无初速释放,摆角很小,问这样的一个摆的周期是多少?
练习 4
固定在天花板上的两根细线与水平面均成 θ 角,线长相等,下端系于同一个小球。给小球一个较小的初速度,让它在前后摆动,小球将作什么运动?能否求出它的周期?
等效摆长:摆球重心到摆动圆弧圆心的距离。
公式拓展1:
L为摆长(或等效摆长)
练习 5
如图,一小球用长为L的细线系于与水平面成α角的光滑斜面内,小球呈平衡状态。若使细线偏离平衡位置,其偏角小于5o,然后将小球由静止释放,则小球的振动周期是多少?
等效重力加速度:等效重力加速度的取值是单摆不振动时,摆线的拉力与摆球质量的比值( g = T/m )。
公式拓展2:
g 为重力加速度(或等效重力加速度)
如图有一带电量为q的小球,用长为 L的绝缘细线悬挂在匀强电场E 中,匀强电场方向与重力方向垂直。小球可视为质点,当小球小角度摆动时,求小球的摆动周期。
(重力加速度为g ,场强 )
练习 6
E
E
一般复合场中,单摆周期
如图所示,单摆甲放在空气中,周期为T甲;单摆乙带正电,放在匀强磁场中,周期为T乙;单摆丙带正电,悬点处有另一带正电q小球,周期T丙。甲、乙、丙的周期关系为( )
A. T甲< T乙< T丙
B. T甲< T丙, T乙不确定
C. T甲=T乙< T丙
D. T甲=T乙=T丙
练习 7
练习8
一单摆,摆长为L,摆球质量为m,悬在升降机顶部。当升降机以加速度a下降时,求单摆在升降机内简谐振动的周期T。
a
a
若升降机以加速度a上升呢?
自主拓展练习
如图所示,摆长为L的单摆悬于架上,架固定于小车,使小车沿倾角为 φ的斜面以加速度a向下做匀加速运动,求此时单摆振动的周期。
参考答案
课间休息 10分钟
周期公式推导
1. 什么是单摆?
摆长 L
摆 角
θ
摆长:悬点到球心的距离。
定义:一根不可伸长的细线下面悬挂一个小球就构成了单摆。
偏角:摆到最高点时,摆线与竖直方向的夹角。
摆球质量m
理想化条件:
单摆是实际摆的理想化模型。
摆线不可伸长
摆线可视为轻绳
摆球可视为质点
空气阻力忽略不计
② 在P点,对摆球受力分析如图所示。
B
A
O
2. 单摆的回复力
摆球的平衡位置在O点;摆球在任一点P点时,摆角为θ,摆球的位移x如图。
大小:
G2=Gsinθ=mg sinθ
方向:
沿切线指向平衡位置
模型:质量为m的摆球在竖直平面内摆动,摆长为l,偏角为α。重力加速度为g。
P
θ
T
G
G2
G1
重力沿切线的分力提供回复力
几何关系
摆角
θ 正弦值
sinθ 弧度值
AB/r
1? 0.01754 0.01745
2? 0.03490 0.03491
3? 0.05234 0.05236
4? 0.06976 0.06981
5? 0.08716 0.08727
7? 0.12187 0.12217
10? 0.17365 0.17445
15? 0.25882 0.26167
20? 0.34202 0.34889
30? 0.50000 0.52334
45? 0.70711 0.78539
60? 0.86603 1.04667
90? 1.00000 1.57079
条件:θ角很小
B
A
O
P
θ
T
G
G2
G1
若单摆的摆角θ很小,则回复力
F = G2=mg sinθ
令 ,回复力 F = - k x
综上,在摆角很小的情况下,单摆做简谐振动。
思考: (多选)
下列有关单摆运动过程中的受力,说法正确的是( )
A.单摆运动的回复力是重力和摆线拉力的合力
B.单摆运动的回复力是重力沿圆弧切线方向的一个分力
C.单摆运动的回复力是摆线拉力的一个分力
D.单摆经过平衡位置时合力为零
E. 摆球在运动过程中仅受到重力和绳子的拉力
沿切线方向:
合力是重力分力G2 ,按效果称为回复力
沿半径方向:
合力是轻绳拉力和重力分力G1之和,按效果称为向心力
思考题拓展
B
A
O
P
θ
T
G
G2
G1
3. 单摆的振动图像
综上,在摆角很小的情况下,单摆做简谐振动。
结论:单摆振动的x-t图象是一条正弦(余弦)函数图像。
4. 单摆的周期
摆球质量m
偏角
摆长 L
单摆的周期可能与哪些因素有关?
?
实验方法:控制变量法
视频1:摆球质量m相同,摆长L相同,观察周期T与振幅的关系?
视频2:振幅相同,摆长L相同,观察周期T与摆球质量m的关系?
视频3:振幅相同,摆球质量m相同,观察周期T与摆长L的关系?
振幅,摆球质量m,摆长L
实验结论:在同一个地点,单摆周期与摆球质量和振幅无关,仅与摆长有关系,且单摆周期与摆长的平方根成正比。
荷兰物理学家惠更斯(1629---1695)通过实验进一步找到:
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
实验表明单摆周期与单摆所在处的重力加速度有关。 g越小,T越大。
O
弹簧振子
单摆
回复力
周期
对所有简谐振动都成立
(1)计时器:利用等时性
惠更斯在1656年首先利用摆的等时性发明了带摆的计时器(1657年获得专利权)。
周期T =2s的单摆叫做秒摆
(2)测定当地的重力加速度
5. 单摆周期的应用
测出单摆的摆长和周期就可求重力加速度
实验:用单摆测定重力加速度
①制作单摆,并确保其做简谐振动
选材:金属小球 、细线(长1 m左右)
操作:固定悬点,单摆从平衡位置拉开一个较小的角度,无初速度释放小球。
②测摆长
刻度尺测摆线长L0
游标卡尺测小球直径d
③测周期
累计法测周期
摆长 L=L0+d/2
④数据处理
方案1:平均值法
方案2:图像法
课堂小结:
一、单摆概念
二、回复力
四、周期
三、图像: 正弦或余弦曲线
① 线的伸缩和质量不计
②小球可看作质点(摆长为悬点到球心的距离)
① F = mg sinθ
② θ 很小时,F=-k x (简谐运动的条件)
五、周期的应用:
实验:用单摆测定重力加速度
钟摆
若单摆的摆长不变,摆球的质量增加为原来的4倍,摆球经过平衡位置的速度变为原来的1/2,则单摆振动的( )
A.频率不变,振幅不变
B.周期不变,振幅改变
C.频率改变,振幅改变
D.周期改变,振幅不变
练习 1
球A在光滑圆弧凹槽的右端,球B在圆弧的圆心。圆弧的半径远大于弧长,且A、B小球可视为质点。A、B同时无初速释放,下列说法正确的是( )
球A先到达O点
球B先到达O点
球A、B同时先到达O点
无法判断
θ
A
练习 2
B
O
练习 3
一小球挂于O点,细线长为l,O点正下方 l /2处有一铁钉。将小球拉至A处无初速释放,摆角很小,问这样的一个摆的周期是多少?
练习 4
固定在天花板上的两根细线与水平面均成 θ 角,线长相等,下端系于同一个小球。给小球一个较小的初速度,让它在前后摆动,小球将作什么运动?能否求出它的周期?
等效摆长:摆球重心到摆动圆弧圆心的距离。
公式拓展1:
L为摆长(或等效摆长)
练习 5
如图,一小球用长为L的细线系于与水平面成α角的光滑斜面内,小球呈平衡状态。若使细线偏离平衡位置,其偏角小于5o,然后将小球由静止释放,则小球的振动周期是多少?
等效重力加速度:等效重力加速度的取值是单摆不振动时,摆线的拉力与摆球质量的比值( g = T/m )。
公式拓展2:
g 为重力加速度(或等效重力加速度)
如图有一带电量为q的小球,用长为 L的绝缘细线悬挂在匀强电场E 中,匀强电场方向与重力方向垂直。小球可视为质点,当小球小角度摆动时,求小球的摆动周期。
(重力加速度为g ,场强 )
练习 6
E
E
一般复合场中,单摆周期
如图所示,单摆甲放在空气中,周期为T甲;单摆乙带正电,放在匀强磁场中,周期为T乙;单摆丙带正电,悬点处有另一带正电q小球,周期T丙。甲、乙、丙的周期关系为( )
A. T甲< T乙< T丙
B. T甲< T丙, T乙不确定
C. T甲=T乙< T丙
D. T甲=T乙=T丙
练习 7
练习8
一单摆,摆长为L,摆球质量为m,悬在升降机顶部。当升降机以加速度a下降时,求单摆在升降机内简谐振动的周期T。
a
a
若升降机以加速度a上升呢?
自主拓展练习
如图所示,摆长为L的单摆悬于架上,架固定于小车,使小车沿倾角为 φ的斜面以加速度a向下做匀加速运动,求此时单摆振动的周期。
参考答案
课间休息 10分钟
周期公式推导
