人教版数学七年级下册7.1.2平面直角坐标系课件(共31张PPT)
文档属性
| 名称 | 人教版数学七年级下册7.1.2平面直角坐标系课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-06 23:25:02 | ||
图片预览







文档简介
(共31张PPT)
规定了原点、正方向和单位长度的直线叫做数轴。
什么是数轴?
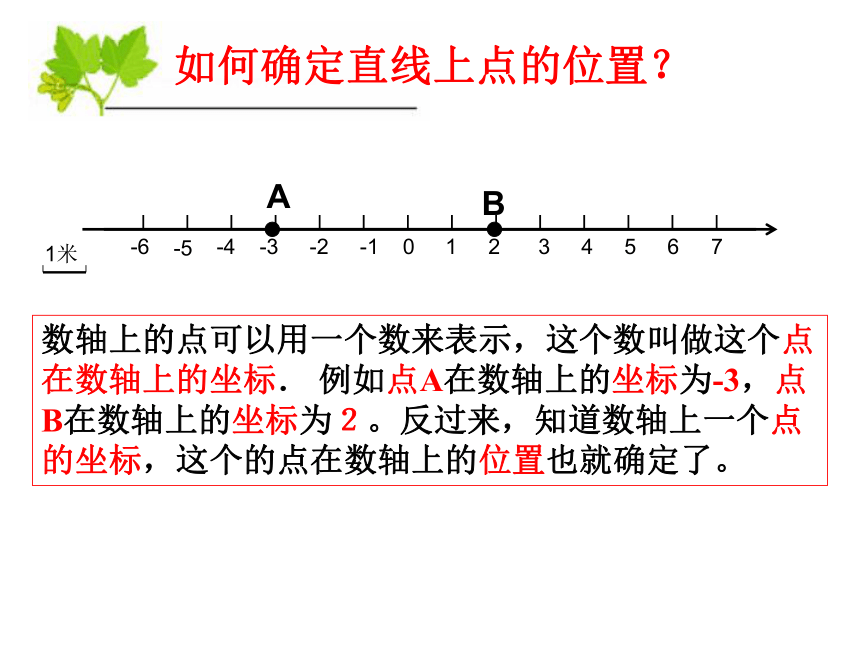
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
如何确定直线上点的位置?
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
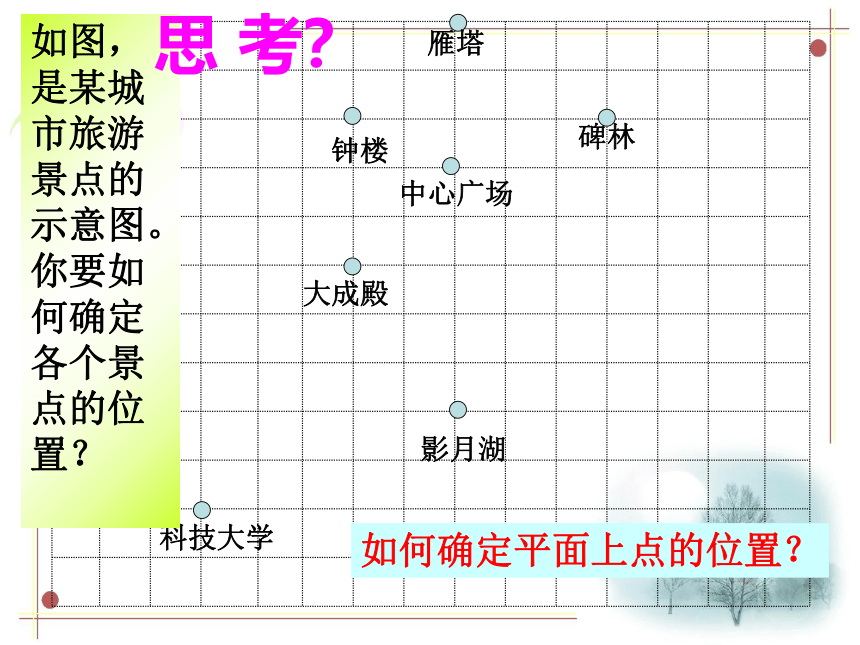
如图,是某城市旅游景点的示意图。你要如何确定各个景点的位置?
如何确定平面上点的位置?
思 考?
笛卡儿, 法国伟大的哲学家、物理学家、数学家。解析几何的创始人。1637年,他发表了《几何学》,创立了直角坐标系。他用平面上的一点到两条固定直线的距离来确定点的位置,用坐标来描述空间上的点。他进而创立了解析几何学,把相互对立着的“数”与“形”统一了起来。人们称他为“近代科学的始祖”。
笛卡儿
7.1.2 平面直角坐标系
1.知识与能力目标:
???? 使学生认识平面直角坐标系,理解并掌握横轴、纵轴、原点及点的坐标,能准确地在平面直角坐标系中描出点的位置和根据点的位置写出点的坐标 ;了解特殊位置的点的坐标特征。
2.过程与方法目标:
??? 通过自主阅读,用游戏活动和动手实践的方式,培养学生自主获取知识的能力,渗透数形结合的数学思想。
3.情感态度价值观目标:
??? 利用游戏、观察、实践、归纳等方法,积淀学生的数学文化涵养,鼓励学生去发现、去思考,使学生认识到数学的科学价值和应用价值,培养热爱数学,勇于探索的精神。
问题1:什么叫平面直角坐标系?
问题2:平面直角坐标系有什么特征?
问题3:什么叫点的坐标?
平面上 组成
平面直角坐标系, 叫x轴(横轴),
取向 为正方向, 叫y轴(纵轴),
取向 为正方向。两坐标轴的交点是平面直角坐标系的 。
两条具有公共原点且互相垂直的数轴
水平的数轴
右
上
竖直的数轴
原点
平面直角坐标系的概念
满足以下条件的两条数轴叫做平面直角坐标系
(1)原点重合
(2)互相垂直
x轴(横轴)
O
第一象限
第二象限
第三象限
第四象限
y轴(纵轴)
坐标原点
注 意:坐标轴上的点不属于任何象限。
(3)通常取向右、向上为正方向
(4)单位长度一般取相同
Ⅰ
Ⅱ
Ⅲ
Ⅳ
X
O
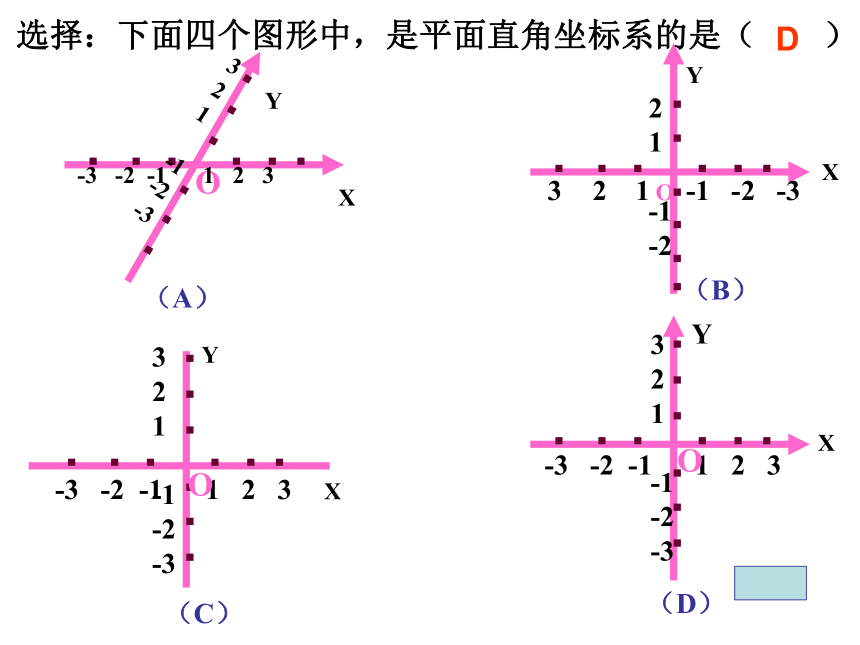
选择:下面四个图形中,是平面直角坐标系的是( )
X
X
Y
(A)
3 2 1 -1 -2 -3
X
Y
(B)
2
1
-1
-2
O
D
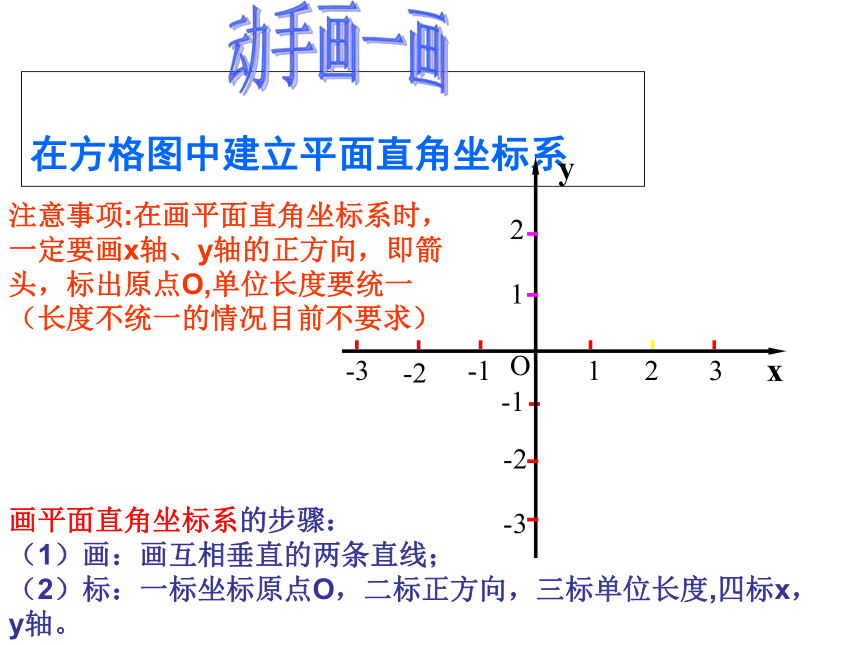
在方格图中建立平面直角坐标系
注意事项:在画平面直角坐标系时,一定要画x轴、y轴的正方向,即箭头,标出原点O,单位长度要统一(长度不统一的情况目前不要求)
画平面直角坐标系的步骤:
(1)画:画互相垂直的两条直线;
(2)标:一标坐标原点O,二标正方向,三标单位长度,四标x,y轴。
X
y
a
b
P(a,b)
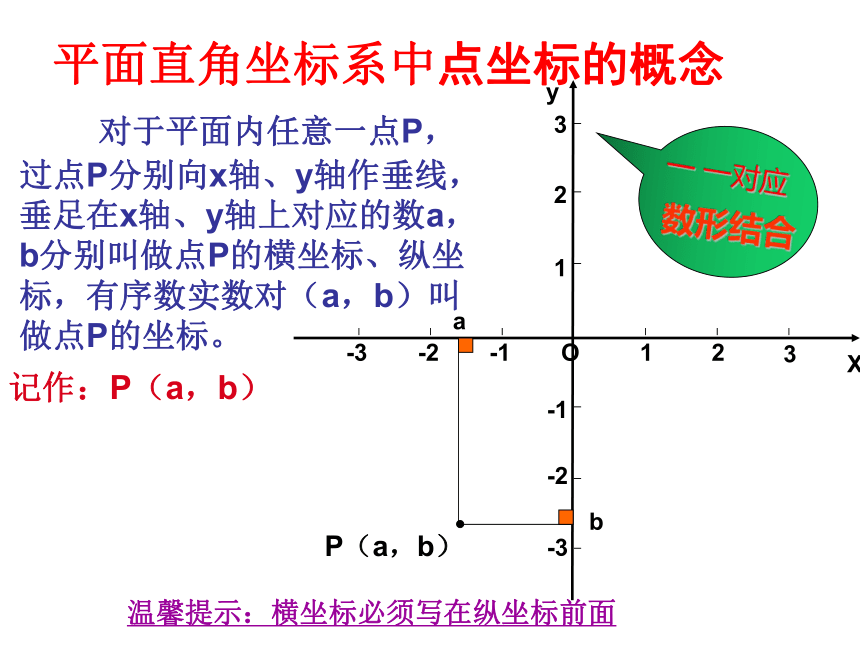
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数实数对(a,b)叫做点P的坐标。
记作:P(a,b)
温馨提示:横坐标必须写在纵坐标前面
根据点求坐标:
平面直角坐标系中点坐标的概念
一 一对应
数形结合
1.由点找坐标:
如何表示点A的位置?
A
(4,3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对
应的数是4,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对
应的数是3,就是点A的纵坐标.
有序数对(4,3)就是点A的坐标.
x
y
在平面直角坐标系中找到表示A(3,-2)的点.
由坐标找点的方法:
先在坐标轴上找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
A
2.由坐标找点(描点):
·
A
·
B
·
E
F
C
D
在平面直角坐标系中描出下列各点
A (4,2) B(-4,1)C (-3,-4)
D (3,-2) E(0,4) F(-3,0)
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
快速说出图中各点的坐标
请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) B (3,-2) C(0,4) D(-6,0) E(1,8) F(0,0) G(5,0) H(-6,-4) M (0,-3)
1.以 A同学 所在排为横轴、以B同学所在列为纵轴建立平面直角坐标系,你能用坐标表示你的位置吗?
2.请找出以下几个坐标指的是哪个同学的位置:(3,2) (-2,4) (0,3) (-3,-4) (4,-1)
3.第一象限的同学请举手!……
点到两轴的距离
点P(x,y)到x轴的距离为∣y∣,到y轴的距离为∣x∣.例如,点A(-3,4)到x轴的距离为4,到y轴的距离为3.
注意:
点P(x,y)到两轴的距离是一个非负数.
例如点A(-3,4)到y轴的距离为3而不是-3
如图,以中心广场为坐标原点,取正东方向为x轴的正方向,取正北方向为y轴的正方向,一个方格的边长作为一个单位长度,建立直角坐标系,分别写出图中各个景点的坐标。
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
各个景点的坐标为:
雁塔(0,3)
碑林(3,1)
钟楼(-2,1)
大成殿(-2,-2)
科技大学(-5,-7)
影月湖(0,-5)
中心广场(0,0)
1.横坐标为负,纵坐标为正的点( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
2.如果a-b<0,且ab<0,那么点(a,b)在
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
3.点A(3,4)到x轴的距离是( ),
到y轴的距离是( );
4.点B(0,9)到x轴的距离是( ),
到y轴的距离是( );
5.点C (9,0)到x轴的距离是( ),
到y轴的距离是( );
4
3
9
0
0
9
6.若点P(a,b)是第四象限的点,且︱a ︱ =2,
︱ b ︱ =3,则p的坐标是( )
A. (2,-3) B.(-2,3)
C.(-3,2) D.(3,-2)
A
已知(a-2)2 + ︱ b+3 ︱=0,
则P(-a,-b)的坐标为----------
(-2,3)
通过今天的学习,你有什么收获?
1.平面直角坐标系的有关概念;
2.建立平面直角坐标系;
3.由点写出坐标,由坐标找出点;
4.平面直角坐标系中坐标轴和各个
象限上的点的坐标的特征。
3
1
4
2
-2
-4
-1
-3
x
y
当点P (a,b)落在一、三或二、四象限的两条坐标轴夹角平分线上时a,b 之间是什么关系?
1.课本第69页第3题(写在书上)
2.作业本:课本第69页第5、6题
数学中的人生哲理
在生命萌动之初,你在人世间就有了自己的位置,到生命终结之际,你在大地上仍有自己的位置。一个人要知道自己的位置,就像知道一个人的脸面一样,这是最为清醒的自觉。所以做能做的事,把它做到最好,这才是做人的重要。
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
各个景点的坐标为:
雁塔(0,3)
碑林(3,1)
钟楼(-2,1)
大成殿(-2,-2)
科技大学(-5,-7)
影月湖(0,-5)
中心广场(0,0)
雁塔
中心广场
钟楼
大成殿
科枝大学
碑林
影月湖
如果以“中心广场”为原点作平面直角坐标系那么你能表示“碑林”的位置吗?“大成殿”的位置呢?
规定了原点、正方向和单位长度的直线叫做数轴。
什么是数轴?
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
如何确定直线上点的位置?
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
如图,是某城市旅游景点的示意图。你要如何确定各个景点的位置?
如何确定平面上点的位置?
思 考?
笛卡儿, 法国伟大的哲学家、物理学家、数学家。解析几何的创始人。1637年,他发表了《几何学》,创立了直角坐标系。他用平面上的一点到两条固定直线的距离来确定点的位置,用坐标来描述空间上的点。他进而创立了解析几何学,把相互对立着的“数”与“形”统一了起来。人们称他为“近代科学的始祖”。
笛卡儿
7.1.2 平面直角坐标系
1.知识与能力目标:
???? 使学生认识平面直角坐标系,理解并掌握横轴、纵轴、原点及点的坐标,能准确地在平面直角坐标系中描出点的位置和根据点的位置写出点的坐标 ;了解特殊位置的点的坐标特征。
2.过程与方法目标:
??? 通过自主阅读,用游戏活动和动手实践的方式,培养学生自主获取知识的能力,渗透数形结合的数学思想。
3.情感态度价值观目标:
??? 利用游戏、观察、实践、归纳等方法,积淀学生的数学文化涵养,鼓励学生去发现、去思考,使学生认识到数学的科学价值和应用价值,培养热爱数学,勇于探索的精神。
问题1:什么叫平面直角坐标系?
问题2:平面直角坐标系有什么特征?
问题3:什么叫点的坐标?
平面上 组成
平面直角坐标系, 叫x轴(横轴),
取向 为正方向, 叫y轴(纵轴),
取向 为正方向。两坐标轴的交点是平面直角坐标系的 。
两条具有公共原点且互相垂直的数轴
水平的数轴
右
上
竖直的数轴
原点
平面直角坐标系的概念
满足以下条件的两条数轴叫做平面直角坐标系
(1)原点重合
(2)互相垂直
x轴(横轴)
O
第一象限
第二象限
第三象限
第四象限
y轴(纵轴)
坐标原点
注 意:坐标轴上的点不属于任何象限。
(3)通常取向右、向上为正方向
(4)单位长度一般取相同
Ⅰ
Ⅱ
Ⅲ
Ⅳ
X
O
选择:下面四个图形中,是平面直角坐标系的是( )
X
X
Y
(A)
3 2 1 -1 -2 -3
X
Y
(B)
2
1
-1
-2
O
D
在方格图中建立平面直角坐标系
注意事项:在画平面直角坐标系时,一定要画x轴、y轴的正方向,即箭头,标出原点O,单位长度要统一(长度不统一的情况目前不要求)
画平面直角坐标系的步骤:
(1)画:画互相垂直的两条直线;
(2)标:一标坐标原点O,二标正方向,三标单位长度,四标x,y轴。
X
y
a
b
P(a,b)
对于平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数实数对(a,b)叫做点P的坐标。
记作:P(a,b)
温馨提示:横坐标必须写在纵坐标前面
根据点求坐标:
平面直角坐标系中点坐标的概念
一 一对应
数形结合
1.由点找坐标:
如何表示点A的位置?
A
(4,3)
如何表示点A的位置:
过点A作x轴的垂线,垂足在x轴上对
应的数是4,就是点A的横坐标.
过点A作y轴的垂线,垂足在y轴上对
应的数是3,就是点A的纵坐标.
有序数对(4,3)就是点A的坐标.
x
y
在平面直角坐标系中找到表示A(3,-2)的点.
由坐标找点的方法:
先在坐标轴上找到表示横坐标与纵坐标的点,
然后过这两点分别作x轴与y轴的垂线,
垂线的交点就是该坐标对应的点。
A
2.由坐标找点(描点):
·
A
·
B
·
E
F
C
D
在平面直角坐标系中描出下列各点
A (4,2) B(-4,1)C (-3,-4)
D (3,-2) E(0,4) F(-3,0)
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
快速说出图中各点的坐标
请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) B (3,-2) C(0,4) D(-6,0) E(1,8) F(0,0) G(5,0) H(-6,-4) M (0,-3)
1.以 A同学 所在排为横轴、以B同学所在列为纵轴建立平面直角坐标系,你能用坐标表示你的位置吗?
2.请找出以下几个坐标指的是哪个同学的位置:(3,2) (-2,4) (0,3) (-3,-4) (4,-1)
3.第一象限的同学请举手!……
点到两轴的距离
点P(x,y)到x轴的距离为∣y∣,到y轴的距离为∣x∣.例如,点A(-3,4)到x轴的距离为4,到y轴的距离为3.
注意:
点P(x,y)到两轴的距离是一个非负数.
例如点A(-3,4)到y轴的距离为3而不是-3
如图,以中心广场为坐标原点,取正东方向为x轴的正方向,取正北方向为y轴的正方向,一个方格的边长作为一个单位长度,建立直角坐标系,分别写出图中各个景点的坐标。
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
各个景点的坐标为:
雁塔(0,3)
碑林(3,1)
钟楼(-2,1)
大成殿(-2,-2)
科技大学(-5,-7)
影月湖(0,-5)
中心广场(0,0)
1.横坐标为负,纵坐标为正的点( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
2.如果a-b<0,且ab<0,那么点(a,b)在
( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
3.点A(3,4)到x轴的距离是( ),
到y轴的距离是( );
4.点B(0,9)到x轴的距离是( ),
到y轴的距离是( );
5.点C (9,0)到x轴的距离是( ),
到y轴的距离是( );
4
3
9
0
0
9
6.若点P(a,b)是第四象限的点,且︱a ︱ =2,
︱ b ︱ =3,则p的坐标是( )
A. (2,-3) B.(-2,3)
C.(-3,2) D.(3,-2)
A
已知(a-2)2 + ︱ b+3 ︱=0,
则P(-a,-b)的坐标为----------
(-2,3)
通过今天的学习,你有什么收获?
1.平面直角坐标系的有关概念;
2.建立平面直角坐标系;
3.由点写出坐标,由坐标找出点;
4.平面直角坐标系中坐标轴和各个
象限上的点的坐标的特征。
3
1
4
2
-2
-4
-1
-3
x
y
当点P (a,b)落在一、三或二、四象限的两条坐标轴夹角平分线上时a,b 之间是什么关系?
1.课本第69页第3题(写在书上)
2.作业本:课本第69页第5、6题
数学中的人生哲理
在生命萌动之初,你在人世间就有了自己的位置,到生命终结之际,你在大地上仍有自己的位置。一个人要知道自己的位置,就像知道一个人的脸面一样,这是最为清醒的自觉。所以做能做的事,把它做到最好,这才是做人的重要。
雁塔
中心广场
钟楼
大成殿
科技大学
碑林
影月湖
各个景点的坐标为:
雁塔(0,3)
碑林(3,1)
钟楼(-2,1)
大成殿(-2,-2)
科技大学(-5,-7)
影月湖(0,-5)
中心广场(0,0)
雁塔
中心广场
钟楼
大成殿
科枝大学
碑林
影月湖
如果以“中心广场”为原点作平面直角坐标系那么你能表示“碑林”的位置吗?“大成殿”的位置呢?
