六年级下册数学课件-圆柱的体积-人教版(共44张PPT)
文档属性
| 名称 | 六年级下册数学课件-圆柱的体积-人教版(共44张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 09:38:06 | ||
图片预览







文档简介
(共44张PPT)
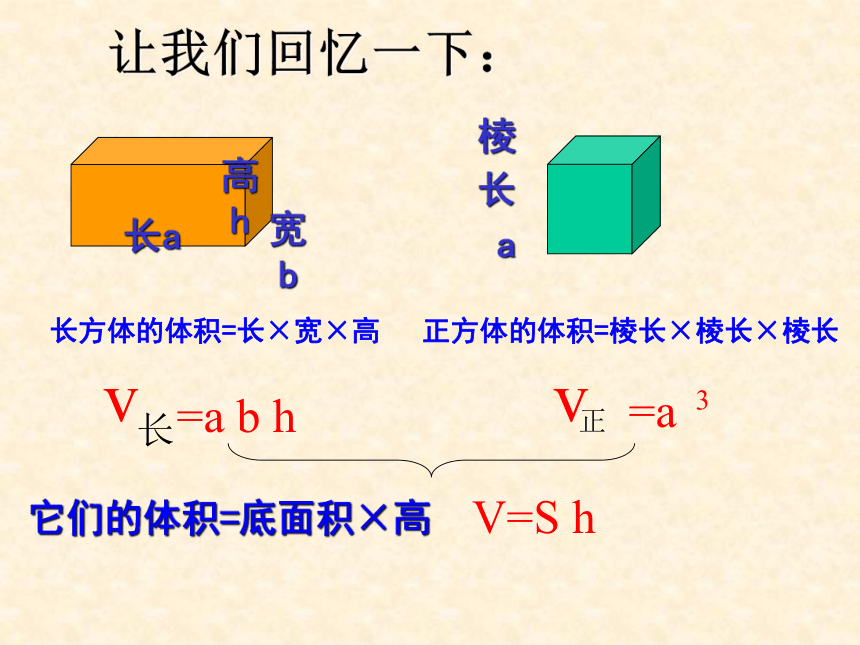
让我们回忆一下:
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=S h
它们的体积=底面积×高
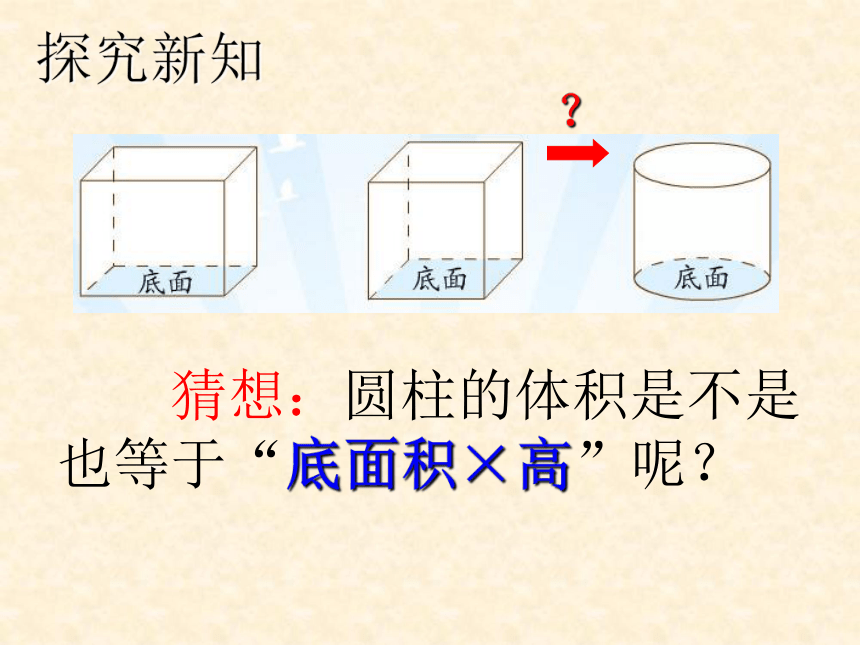
猜想:圆柱的体积是不是也等于“底面积×高”呢?
?
探究新知
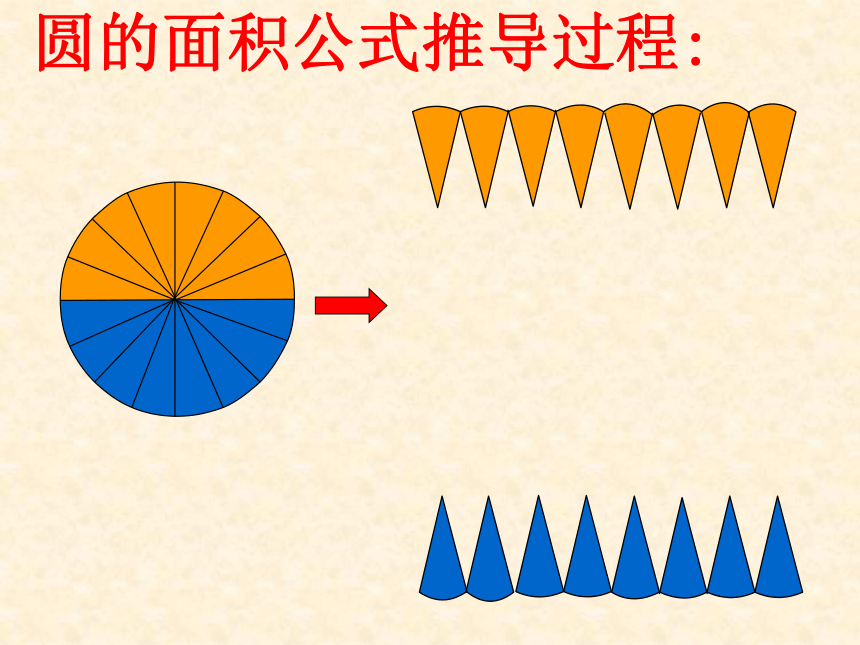
想一想:
在学习计算圆的面积时,我们是怎样把圆变成已学过的图形来计算面积的
?
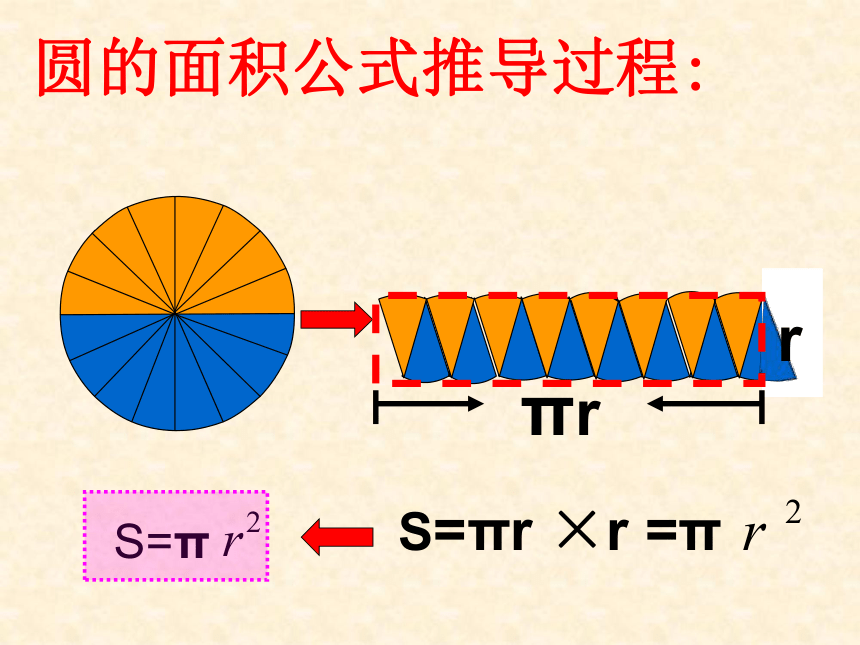
圆的面积公式推导过程:
πr
r
圆的面积公式推导过程:
讨论:
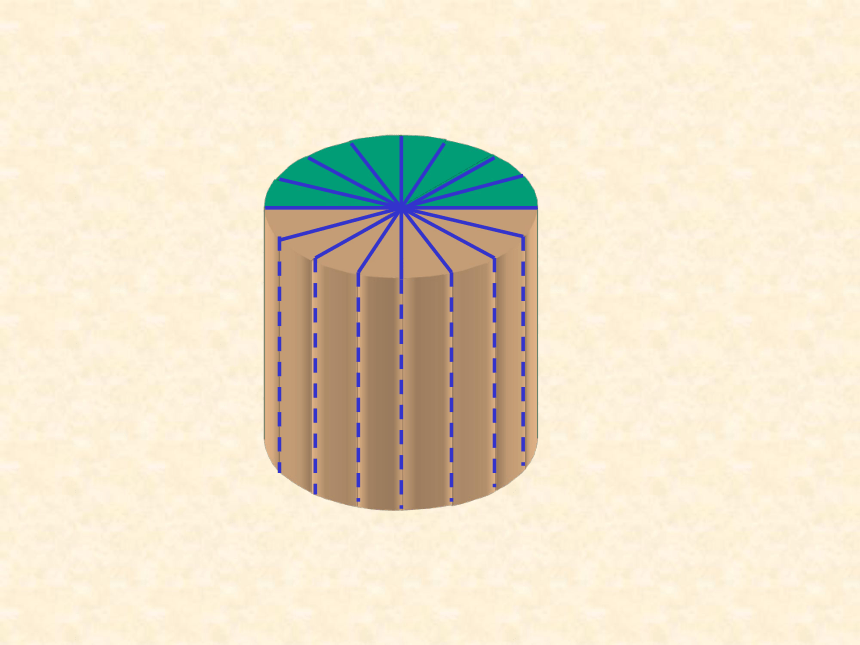
能不能把圆柱转化成我们已经学过的形体来求出它的体积?
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
1.长方体的底面积与圆柱的底面积有什么关系?
2.长方体的高与圆柱的高有什么关系?
3.长方体的体积与圆柱的体积有什么关系?
拼成的长方体与原来的圆柱有什么联系?
概括:
试着根据圆柱与近似长方体的关系,推导公式:
长方体的体积=底面积×高
↓ ↓ ↓
圆 柱 的 体积=底面积×高
用字母表示计算公式: V=Sh
思考:
求圆柱的体积必须具备哪两个条件?
9dm=90cm
75 ×90 =6750(cm3)
答:它的体积是6750cm3。
1. 一根圆柱形木料,底面积为75cm2 ,长9dm。它的体积是多少?
思考:这道题已知什么?求什么?能不能根据公式直接计算?计算之前要注意什么?
杯子的容积。
请你想一想,要回答这个问题,先要计算出什么?
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
答:因为502.4大于498,所以杯子能装下这袋牛奶。
杯子的容积: 50.24×10
=502.4 (cm3 )
=502.4 (mL)
巩固练习
一、填表。
15
3
45
40
4
160
底面积 s
(平方米) 高 h
(米) 圆柱体积 V
(立方米)
二、填空
1、一个长方体和一个圆柱的体积
相等,高也相等,那么它们的
底面积( )。
2、一根横截面面积是10平方厘米
的圆柱形钢材,长是2米,它的
体积是( )立方厘米。
相等
2000
三、判断对错。
一根圆柱形钢材,底面积是50cm ,高是2.1m。求它的体积?
2
A、50 ×2.1=105(cm )
B、2.1m=210cm 50 ×210=10500(cm )
C、50cm =0.5m 0.5 ×2.1=1.05(m )
D、50cm =0.005 (m )
0.005 ×2.1=0.105(m )
3
3
3
3
2
2
2
2
四、求下面圆柱的体积。(只列式不计算。)
1、底面积24平方厘
米,高12厘米。
2
2、底面半径 2 厘
米, 高 5 厘米。
5
12
24×12
3.14×
× 5
3、底面直径 5 分米, 高 2 分米。
2
3.14×
÷ × 2
5
保温杯的容积:
50.24×15
=753.6 (cm?)
=0.7536(L)
答:因为0.7536小于1,所以带这杯水不够喝。
4. 小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
拓展提高:
一个圆柱的石柱子底面的周长18.84分米,高是20分米, 体积是多少?
全课总结
问:这节课里我们学到了哪些知识?
作业:第26页做一做,第2题。
第28页练习五,第2题、第6题。
布置作业
让我们回忆一下:
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
V=S h
它们的体积=底面积×高
猜想:圆柱的体积是不是也等于“底面积×高”呢?
?
探究新知
想一想:
在学习计算圆的面积时,我们是怎样把圆变成已学过的图形来计算面积的
?
圆的面积公式推导过程:
πr
r
圆的面积公式推导过程:
讨论:
能不能把圆柱转化成我们已经学过的形体来求出它的体积?
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
1.长方体的底面积与圆柱的底面积有什么关系?
2.长方体的高与圆柱的高有什么关系?
3.长方体的体积与圆柱的体积有什么关系?
拼成的长方体与原来的圆柱有什么联系?
概括:
试着根据圆柱与近似长方体的关系,推导公式:
长方体的体积=底面积×高
↓ ↓ ↓
圆 柱 的 体积=底面积×高
用字母表示计算公式: V=Sh
思考:
求圆柱的体积必须具备哪两个条件?
9dm=90cm
75 ×90 =6750(cm3)
答:它的体积是6750cm3。
1. 一根圆柱形木料,底面积为75cm2 ,长9dm。它的体积是多少?
思考:这道题已知什么?求什么?能不能根据公式直接计算?计算之前要注意什么?
杯子的容积。
请你想一想,要回答这个问题,先要计算出什么?
下图的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
答:因为502.4大于498,所以杯子能装下这袋牛奶。
杯子的容积: 50.24×10
=502.4 (cm3 )
=502.4 (mL)
巩固练习
一、填表。
15
3
45
40
4
160
底面积 s
(平方米) 高 h
(米) 圆柱体积 V
(立方米)
二、填空
1、一个长方体和一个圆柱的体积
相等,高也相等,那么它们的
底面积( )。
2、一根横截面面积是10平方厘米
的圆柱形钢材,长是2米,它的
体积是( )立方厘米。
相等
2000
三、判断对错。
一根圆柱形钢材,底面积是50cm ,高是2.1m。求它的体积?
2
A、50 ×2.1=105(cm )
B、2.1m=210cm 50 ×210=10500(cm )
C、50cm =0.5m 0.5 ×2.1=1.05(m )
D、50cm =0.005 (m )
0.005 ×2.1=0.105(m )
3
3
3
3
2
2
2
2
四、求下面圆柱的体积。(只列式不计算。)
1、底面积24平方厘
米,高12厘米。
2
2、底面半径 2 厘
米, 高 5 厘米。
5
12
24×12
3.14×
× 5
3、底面直径 5 分米, 高 2 分米。
2
3.14×
÷ × 2
5
保温杯的容积:
50.24×15
=753.6 (cm?)
=0.7536(L)
答:因为0.7536小于1,所以带这杯水不够喝。
4. 小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
拓展提高:
一个圆柱的石柱子底面的周长18.84分米,高是20分米, 体积是多少?
全课总结
问:这节课里我们学到了哪些知识?
作业:第26页做一做,第2题。
第28页练习五,第2题、第6题。
布置作业
