北师大版七年级数学下册 4.3 探索三角形全等的条件课件(共两课时,共63张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.3 探索三角形全等的条件课件(共两课时,共63张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 49.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览









文档简介
(共63张PPT)
初中数学七年级(下)
4.3 探索三角形全等的条件
温故知新:
1.什么叫做全等三角形?
能够完全重合的两个三角形叫做全等三角形.
2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
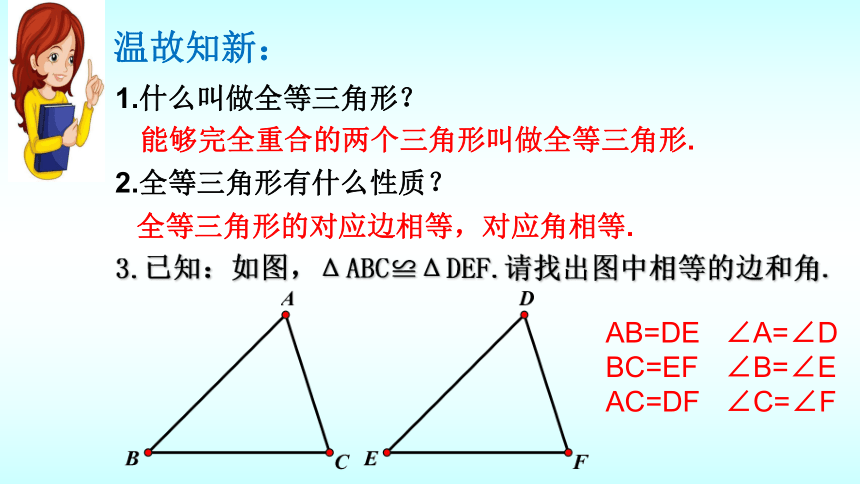
3.已知:如图,ΔABC≌ΔDEF.请找出图中相等的边和角.
AB=DE
BC=EF
AC=DF
∠A=∠D
∠B=∠E
∠C=∠F
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?
问题引入:
探究活动1:
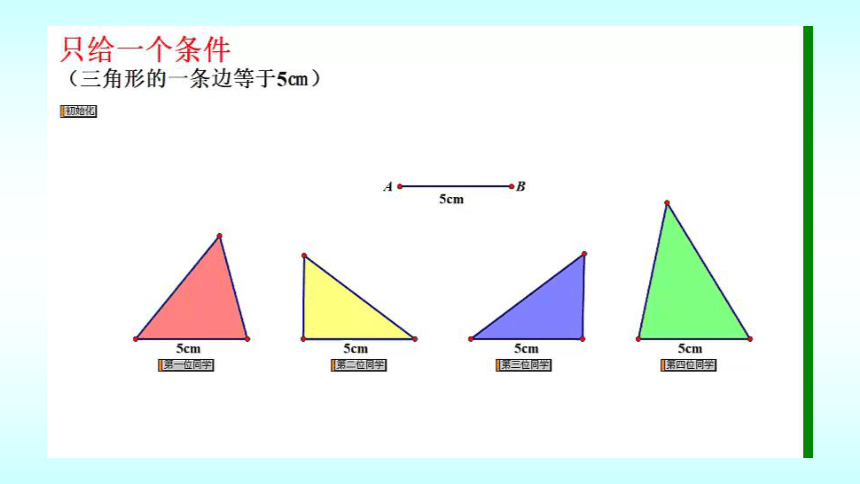
只给一个条件(一条边或一个角)画三角形时,
大家画出的三角形一定全等吗?
请按照下面的条件画一画
(1)请画一个三角形,其中一条边的长度是5㎝;
(2)请画一个三角形,其中一个角的度数是30°.
探究结论1:
一个条件不能保证三角形全等
探究活动2:
想一想:给出两个条件画三角形时,有几种可能的情况?
一角一边,两角或者两边。
请按照下面的条件画一画
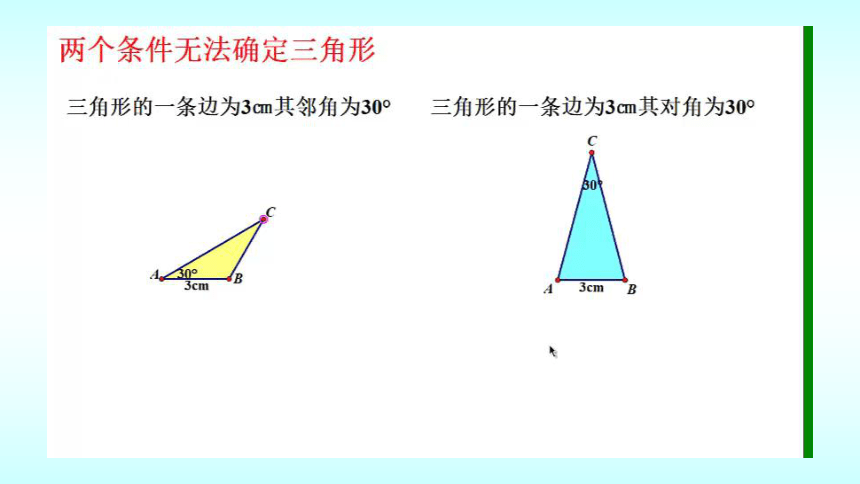
(1)三角形的一个内角为30°,一条边为3cm;
(2)三角形的两个内角分别为30°和 50°;
(3)三角形的两条边分别为4cm,6cm.
探究结论2:
两个条件不能保证三角形全等
探究活动3:
想一想:给出三个条件画三角形时,
你能说出有哪几种可能的情况吗?
三角、三边、两角一边和两边一角,一共四种情况。
(1)已知一个三角形的三个内角分别为40°,60°和80°,
你能画出这个三角形吗?
把你画的三角形与同伴画出的进行比较,它们一定全等吗?
请按照下面的条件画一画
(2)已知一个三角形的三条边分别为4cm,5cm和7cm,
你能画出这个三角形吗?
(请大家准备4cm,5cm和7cm长的的三条硬纸条或小木棒,拼出一个三角形)
把你拼的三角形与同伴拼出的进行比较,它们一定全等吗?
探究活动3:
请按照下面的条件画一画
探究结论3:
1.三个内角分别相等的两个三角形不一定全等。
2.三边分别相等的两个三角形全等,
简写为“边边边”或“SSS”。
几何语言的表述:
在△ABC和△DEF中
AB=DE,
AC=DF,
BC=EF.
∴△ABC≌△DEF
探究活动4:
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
动手做一做
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?
探究结论4:
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
四边形的框架,它的大小和形状是可以改变的,四边形不具备稳定性。
你能举几个应用三角形稳定性的例子吗?
跪姿射击的稳定性
如何据枪最稳固?结合力的构成,
跪姿据枪的要领概括为“三三据枪法”:第一个三,就是支撑身体、稳固据枪的三个三角形:左脚、右脚尖、右膝构成水平三角形,起到稳固支撑身体的作用;左手、左肘、左肩构成垂直三角形,起到稳固托枪的作用;左手、左肩、右肩构成水平三角形,起到稳固据枪的作用。
第二个三,就是“三心重叠”:枪的重心,身体的重心,与身体支撑面三角形的中心重叠。两手对枪的作用力始终水平向后。身体和枪在重心的牵引下,通过力的三角形将身体锁住,这样据枪最稳固。
如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线。你能说明其中的道理吗?
A(R)
B
D
C
E
Q
P
问题解决:
小明的思考过程如下:
你能说出每一步的理由吗?
在△ABC和△ADC中,
因为AB=AD,BC=DC,AC=AC.
所以△ABC ≌△ADC,
所以∠BAC=∠DAC,即∠QRE=∠PRE.
所以AE就是∠PRQ的角平分线 .
课堂小结:
一、知识技能
(1)边边边判定三角形全等的方法;
(2)三角形稳定性的性质。
二、数学思考
(1)分类讨论思想;
(2)举反例的方法。
三、问题解决
通过观察、动手操作、类比、推断等数学活动,积累数学
活动经验,感受数学思考过程的条理性,发展形象思维。
四、情感态度
通过自主学习的发展体验获取数学知识的感受,
培养勇于创新,多方位审视问题的创造技巧。
4.3 探索三角形全等的条件
(第2课时)
小明在家锻炼时,不小心用球将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢? 如果可以,带哪块去合适? 为什么? 请同学们帮他想一想.
情境创设 问题驱动
情境创设 问题驱动
A
B
只给出一个或两个条件时,是不能保证做出的三角形与原来三角形全等的。
要保证做出的三角形与原来三角形全等,至少需要边或角的三个条件:
(2) 三条边
(1) 三个角
(3) 两角一边
SSS
不能!
?
(4) 两边一角
探究发现 形成新知
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
“两角及夹边”
“两角和其中一角的对边”
分类讨论
探究发现 形成新知
若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?
2cm
60°
80°
你画的三角形与老师画的三角形一定全等吗?
探究过程
作图探究
改变角度和边长,你能得到同样的结论吗?
探究发现 形成新知
几何语言:
在△ABC 和△ A′B′ C′中,
∴△ABC ≌△ A′B′ C′(ASA).
∠A =∠A′,
AB = A′B′,
∠B =∠B′,
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
A
B
C
A'
B'
C'
判定三角形全等的方法
在△ABC和△DEF中, ∠A=∠D,∠B=∠E,BC=EF,
求证△ABC ≌△DEF.
你能从上题中得到什么结论?
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
A
B
C
D
E
F
证明:在△ABC 中,
∵∠A +∠B +∠C =180°
∴∠C = 180°-∠A-∠B
又 ∵∠A =∠D, ∠B =∠E,
∴∠C = ∠F
在△ABC 和△DEF 中,
∴△ABC ≌△DEF(ASA).
∠B=∠E,
BC = EF,
∠C =∠F,
同理可得∠F =180°-∠D -∠E
判定三角形全等的方法
只要两个三角形的两角一边对应相等,这两个三角形全等.
ASA
AAS
(三角形内角和定理)
归纳总结 巩固新知
例题讲解
如图,AB与CD相交于点O,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
A
B
C
D
O
解: △AOC≌△BOD.
在△AOC和△BOD中,
∴△AOC≌△BOD(ASA).
∠A =∠B,
AO = BO,
∠AOC =∠BOD,
理由如下: ∵O是AB的中点,
∴AO=BO
问题变式 思维拓展
变式一
A
B
C
D
O
A
B
C
D
E
F
如图∠A=∠B,∠AFC=∠BED,那么要得到△ACF≌△BDE,还应给出的条件是( )
A.∠C=∠D B.AC=ED
C.CF=BD D.AE=BF
注意:
要判定两个三角形全等时,边和角一定要“对应相等”,而不是“相等”.
D
∵AE=BF,
∴AE-EF=BF-EF
即 AF=BE
问题变式 思维拓展
变式二
A
B
C
D
O
A
B
C
D
E
F
提示:
如图AF=BE,AC∥BD,∠C=∠D,求证CF∥ED
由线平行可推出角相等,由角相等推出线平行.
∠A=∠B,
∠C =∠D,
AF= BE,
∴△ACF ≌△BDE(AAS).
∴∠AFC=∠BED
∴CF∥ED
证明:∵AC∥BD
∴∠A=∠B
在△ACF 和△BDE 中,
找条件,证全等
1.直接条件:
2.隐含条件:
3.间接条件:
A
B
C
D
E
F
∟
∟
归纳总结 巩固新知
即已知中直接给出的三角形的对应边或对应角.
即已知没有给出,但通过读图很容易得到的条件,
如公共边、公共角、对顶角等.
即已知中所给条件不是三角形的边和角,需要进一步推理.比如
平行、角平分线、垂直等都可得到角相等.中点、等式的基本性质
可推出线段相等等.
学以致用 思维提升
E
M
B
A
F
O
N
C
如图,O是线段EF的中点,∠E=∠F,∠A=∠B,
求证:△EOB≌△FOA
△AON≌△BOM
△ACM≌△BCN
AAS
ASA
AAS、ASA
证明两个三角形全等判定方法不一定是唯一的!根据条件选择合适的即可.
△EOM≌△FON
SSS、ASA、AAS
图中还有其他的全等三角形吗?请说明理由.
步步高
全等
全等
边、角相等
∵AO=BO,MO=NO
∴AO-MO=BO-NO
即 AM=BN
问题驱动 回扣情境
A
B
要保证做出的三角形与原来三角形全等,至少需要边或角的三个条件:
(2) 三条边
(1) 三个角
(3) 两角一边
SSS
不能!
(4) 两边一角
带B. 由“角边角”可知,利用这块能配出一个与原来全等的三角形玻璃.
ASA
AAS
课堂小结 反思提升
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”.
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
探索三角形全等的条件
思想方法
要学会分类、转化等思想解决问题.
(SSS、ASA、AAS)
文化渗透 课外拓展
古人对全等三角形的认识源于测量.据史料记载.第一个应用全等三角形的人应该是古希腊学者泰勒斯(约公元前625一公元前547).他可谓是几何学的鼻祖,把演绎逻辑思想引入数学.尤其值得称道的是,他证明了第一个全等三角形的判定定理:也就是我们今天所研究的“角边角”定理.
有关全等三角形判定的历史追溯
古希腊数学家欧几里得试图利用较为严密的逻辑推理去推证全等的相关结论.“直觉是不可靠的”和“几何中无王者之路”是他的名言.欧几里得没有利用三角形内角和定理.而是分别对“等角夹边”和“等角对边”两种情况进行了证明,其中也应用了反证法. 有些数学家不满意欧几里得的证明.如阿拉伯数学家阿尔·奈里兹(865--922)在注释《原本》时,仍采用了叠置法.
文化渗透 课外拓展
有关全等三角形判定的历史追溯
对于同一个问题,数学家们虽然会有不同的见解.但在他们学术个性的背后仍存有共性,即甘于寂寞、坚韧不拔潜心钻研的精神值得我们学习.
在这特殊的阶段,相信同学们也会耐得住寂寞,不断学习,用知识缝制铠甲,不远的将来,当你们走向社会,各行各业都将由你们披甲上阵.加油!
新课引入
我们讨论这种情形:如果两个三角形有两条边和一个角分别对应相等,
那么这两个三角形一定全等吗?又有几种情况呢?
温馨提示
不重不漏哦!
两条边及其中一边的对角
两条边及两边的夹角(两边夹角)
探究体验
画一个三角形,两条边分别为2.5cm,3.5cm ,它们所夹的角为40 °
1.画一线段AB,使它等于3.5cm ;
2.画∠MAB = 40°;
3.在射线AM上截取AC =2.5cm ;
4.连结BC.
△ABC 就是所求的三角形.
A
B
M
C
.
3.5cm
.
.
2.5cm
.
.
实践检验
你画的三角形与同伴画的一定全等吗?
实践检验
A
B
C
A’
B’
C’
结论:
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等.
真真假假
以2.5厘米、3.5厘米为三角形的两边,长度2.5厘米的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?
步骤:1.画一线段AC ,使它等于3.5厘米;
2.画∠CAM = 45°;
3.以C 为圆心, 2.5厘米长为半径画弧,
交AM 于点B.
4.连结CB.
△AB1 C 与△AB2 C 都符合所
要求作的三角形.
结论:两边及其一边所对的角相等,两个三角形无法确定全等.
C
A
B1
B2
.
M
3.5厘米
2.5厘米
2.5厘米
归纳结论
在两个三角形中,如果有两条边及它们的夹角对应
相等,那么这两个三角形全等,简记为SAS.
A
B
C
A’
B’
C’
几何语言
∵ AC = A’C’
∠A = ∠A’
AB = A’B’
∴ △ABC≌△A’B’C’ (SAS )
牛刀小试
在下列图中找出全等三角形,并把它们用直线连起来.
30?
8 cm
9 cm
30?
8 cm
8 cm
30?
8 cm
5 cm
8 cm
5 cm
30?
Ⅲ
30?
8 cm
8 cm
8 cm
5 cm
30?
5 cm
8 cm
Ⅳ
8 cm
9 cm
例题讲解
例1:如图,已知AB =AD,AC =AE,∠BAC =∠DAE,
说明△BAC 与△DAE 全等的理由.
AB =AD(已知)
∠BAC =∠DAE(已知)
AC =AE(已知)
∴△BAC≌△DAE(SAS)
A
D
E
在△ BAC 与△ DAE 中,
说明:
B
C
B
C
例2:如图,AB =AC,BE =CD.
试说明.
(1)△ABD ≌△ACE
(2)BD =CE
(3)∠B =∠C
例题讲解
B
C
A
D
E
AB =AC(已知)
∠A =∠A(公共角)
AD =AE(已证)
∴△ABD≌△ACE(SAS)
在△ABD 与△ACE 中,
(1)
∵ AB =AC,BE =CD
∴ AB –BE =AC-CD
即 AE =AD
(2)
∵ △ABD≌△ACE(已证)
∴BD =CE(全等三角形的对应边相等)
(3)∵ △ABD≌△ACE(已证)
∴∠B =∠C
说明
变式训练
1.如图,已知AB =AD,AC =AE, ∠BAD =∠CAE,
说明△BAC 与△DAE 全等的理由.
A
B
C
D
E
说明:
∵ ∠BAD =∠CAE
∴ ∠BAD -∠CAD =∠CAE -∠CAD
∴ ∠BAC =∠DAE
在△BAC 与△DAE 中,
AB =AD(已知)
∠BAC =∠DAE(已证)
AC =AE(已知)
∴△BAC ≌△ DAE (SAS)
2 .如图,已知AB =DC,∠ABC =∠DCB,那么△ABC 与△DCB
是否全等?为什么?
变式训练
A
B
D
C
△ABC 与△DCB 全等
说明:
在△ABC 与△DCB 中,
AB =DC(已知)
∠ABC =∠DCB (已知)
BC =CB(公共边)
∴△ABC≌△DCB (SAS)
3 . 如图,AB∥DE,
AB =DE,BE =CF
(1) BC =EF
(2)△ABC≌△DEF
(3)AC∥DF
变式训练
A
B
C
E
F
D
AB =DE(已知)
∠ABC =∠DEF (已证)
BC =EF(已证)
∴△ABC ≌△DEF(SAS)
在△ABC与△DEF中,
(1)说明:
∵ BE =CF
∴ BE +EC =CF +EC
∴ BC =EF
∵△ABC≌△DEF (已证)
(3)解:∵ △ ABD≌△ ACE(已证)
∴∠B=∠C(全等三角形的对应角相等)
(2)说明:
∵ AB∥DE
∴ ∠ABC =∠DEF
(3)说明
∴ ∠ACB =∠DFE(全等三角形的对应角相等)
∴ AC ∥ DF
试说明:
拓展提升
如图,已知AB =AE, ∠B =∠E, BC=ED,F是CD 的中点,试说明AF ⊥CD.
A
C
B
D
E
F
拓展提升
A
C
B
D
E
F
在△ABC 与△AED 中
AB = AE
∠B = ∠E
BC = ED
∴ △ABC ≌△AED (SAS)
在△ACF 与△ADF 中
AC =AD
AF = AF
CF =DF
∴ △ACF ≌△ADF (SSS)
∴ ∠AFC =∠AFD
又∵ F是CD 的中点
∴CF =DF
说明:连接AC,AD
∵ ∠AFC +∠AFD = 1800
∴ ∠AFC =∠AFD = 900
∴ AF ⊥CD
∴AC =AD
1.如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC =DF, ∠C =∠F, BC =EF ;
课堂检测
A
E
D
F
C
B
能
能
A
B
C
D
(2) BC =BD, ∠ABC =∠ABD.
2.小明做了一个如图所示的风筝,其中∠EDH =∠FDH, ED =FD ,将上述
条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流.
课堂检测
F
D
H
E
ED =FD
∠EDH =∠FDH(已知)
DH = DH(公共边)
∴△EDH ≌△FDH (SAS)
∴EH =FH(全等三角形对应边相等)
说明:在△EDH 和△FDH 中
3.如图,已知AB 和CD 相交与O, OA=OB, OC =OD.说明 AD ∥ BC.
课堂检测
O
A
B
C
D
1
2
说明:在△OAD 和△OBC中
OA = OB(已知)
∠1 = ∠2(对顶角相等)
OD = OC (已知)
∴△OAD ≌△OBC (SAS)
∴ ∠A = ∠B
∴ AD ∥ BC
学习收获
4、遇到较为复杂的图形时,可以采用图形分离法(将基本图形分离).
3、注意对应边和对应角的确定,特别是公共边和公共角的应用.
2、注意规范书写证明三角形全等的基本步骤.
1、新的一个三角形全等的判定方法:在两个三角形中,如果有两条边 及它们的夹角对应相等,那么这两个三角形全等(简记为SAS).
5、无法直接证明三角形全等时,考虑辅助线的添加.
学习收获
常用到的全等的基本图形
O
A
B
C
D
A
B
C
D
E
A
B
C
D
A
B
C
E
F
D
1.如图,点E 在AB上,AC =AD, ∠CAB =∠DAB , △ACE 与△DAE 全等吗?
课后作业
B
D
A
C
E
△ACB 与△ADB 呢? 请说明理由.
2.如图,已知AB =AD,AC =AE,BA⊥DA,AC⊥AE,
说明△BAC 与△DAE 全等的理由.
A
B
C
D
E
课后作业
3.小颖作业本上画的三角形被墨迹污染,她想画出一个与原来完全一样
的三角形,她该怎么办呢?请帮助小颖想出一个办法来,并说明理由.
课后作业
4.如图, △EFG 的三条边相等,三个内角也相等,且EH =FI =GJ,
△EHJ, △FIH, △GJI全等吗? △HIJ 的三边相等吗?
课后作业
E
I
H
J
G
F
提升题:
有一块三角形木板,如图,由于实际生产的需要,工人师傅要把∠MON
平分开,现在他手边只有一根细绳和一把直尺,你能帮助工人师傅想个
办法吗?并说明理由.
M
O
N
课后作业
初中数学七年级(下)
4.3 探索三角形全等的条件
温故知新:
1.什么叫做全等三角形?
能够完全重合的两个三角形叫做全等三角形.
2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
3.已知:如图,ΔABC≌ΔDEF.请找出图中相等的边和角.
AB=DE
BC=EF
AC=DF
∠A=∠D
∠B=∠E
∠C=∠F
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件?只知道一个条件行吗?两个条件呢?三个条件呢?
问题引入:
探究活动1:
只给一个条件(一条边或一个角)画三角形时,
大家画出的三角形一定全等吗?
请按照下面的条件画一画
(1)请画一个三角形,其中一条边的长度是5㎝;
(2)请画一个三角形,其中一个角的度数是30°.
探究结论1:
一个条件不能保证三角形全等
探究活动2:
想一想:给出两个条件画三角形时,有几种可能的情况?
一角一边,两角或者两边。
请按照下面的条件画一画
(1)三角形的一个内角为30°,一条边为3cm;
(2)三角形的两个内角分别为30°和 50°;
(3)三角形的两条边分别为4cm,6cm.
探究结论2:
两个条件不能保证三角形全等
探究活动3:
想一想:给出三个条件画三角形时,
你能说出有哪几种可能的情况吗?
三角、三边、两角一边和两边一角,一共四种情况。
(1)已知一个三角形的三个内角分别为40°,60°和80°,
你能画出这个三角形吗?
把你画的三角形与同伴画出的进行比较,它们一定全等吗?
请按照下面的条件画一画
(2)已知一个三角形的三条边分别为4cm,5cm和7cm,
你能画出这个三角形吗?
(请大家准备4cm,5cm和7cm长的的三条硬纸条或小木棒,拼出一个三角形)
把你拼的三角形与同伴拼出的进行比较,它们一定全等吗?
探究活动3:
请按照下面的条件画一画
探究结论3:
1.三个内角分别相等的两个三角形不一定全等。
2.三边分别相等的两个三角形全等,
简写为“边边边”或“SSS”。
几何语言的表述:
在△ABC和△DEF中
AB=DE,
AC=DF,
BC=EF.
∴△ABC≌△DEF
探究活动4:
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
动手做一做
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?
探究结论4:
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
四边形的框架,它的大小和形状是可以改变的,四边形不具备稳定性。
你能举几个应用三角形稳定性的例子吗?
跪姿射击的稳定性
如何据枪最稳固?结合力的构成,
跪姿据枪的要领概括为“三三据枪法”:第一个三,就是支撑身体、稳固据枪的三个三角形:左脚、右脚尖、右膝构成水平三角形,起到稳固支撑身体的作用;左手、左肘、左肩构成垂直三角形,起到稳固托枪的作用;左手、左肩、右肩构成水平三角形,起到稳固据枪的作用。
第二个三,就是“三心重叠”:枪的重心,身体的重心,与身体支撑面三角形的中心重叠。两手对枪的作用力始终水平向后。身体和枪在重心的牵引下,通过力的三角形将身体锁住,这样据枪最稳固。
如图,仪器ABCD可以用来平分一个角,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们落在角的两边上,沿AC画一条射线AE,AE就是∠PRQ的平分线。你能说明其中的道理吗?
A(R)
B
D
C
E
Q
P
问题解决:
小明的思考过程如下:
你能说出每一步的理由吗?
在△ABC和△ADC中,
因为AB=AD,BC=DC,AC=AC.
所以△ABC ≌△ADC,
所以∠BAC=∠DAC,即∠QRE=∠PRE.
所以AE就是∠PRQ的角平分线 .
课堂小结:
一、知识技能
(1)边边边判定三角形全等的方法;
(2)三角形稳定性的性质。
二、数学思考
(1)分类讨论思想;
(2)举反例的方法。
三、问题解决
通过观察、动手操作、类比、推断等数学活动,积累数学
活动经验,感受数学思考过程的条理性,发展形象思维。
四、情感态度
通过自主学习的发展体验获取数学知识的感受,
培养勇于创新,多方位审视问题的创造技巧。
4.3 探索三角形全等的条件
(第2课时)
小明在家锻炼时,不小心用球将一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形玻璃呢? 如果可以,带哪块去合适? 为什么? 请同学们帮他想一想.
情境创设 问题驱动
情境创设 问题驱动
A
B
只给出一个或两个条件时,是不能保证做出的三角形与原来三角形全等的。
要保证做出的三角形与原来三角形全等,至少需要边或角的三个条件:
(2) 三条边
(1) 三个角
(3) 两角一边
SSS
不能!
?
(4) 两边一角
探究发现 形成新知
如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
“两角及夹边”
“两角和其中一角的对边”
分类讨论
探究发现 形成新知
若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?
2cm
60°
80°
你画的三角形与老师画的三角形一定全等吗?
探究过程
作图探究
改变角度和边长,你能得到同样的结论吗?
探究发现 形成新知
几何语言:
在△ABC 和△ A′B′ C′中,
∴△ABC ≌△ A′B′ C′(ASA).
∠A =∠A′,
AB = A′B′,
∠B =∠B′,
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
A
B
C
A'
B'
C'
判定三角形全等的方法
在△ABC和△DEF中, ∠A=∠D,∠B=∠E,BC=EF,
求证△ABC ≌△DEF.
你能从上题中得到什么结论?
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
A
B
C
D
E
F
证明:在△ABC 中,
∵∠A +∠B +∠C =180°
∴∠C = 180°-∠A-∠B
又 ∵∠A =∠D, ∠B =∠E,
∴∠C = ∠F
在△ABC 和△DEF 中,
∴△ABC ≌△DEF(ASA).
∠B=∠E,
BC = EF,
∠C =∠F,
同理可得∠F =180°-∠D -∠E
判定三角形全等的方法
只要两个三角形的两角一边对应相等,这两个三角形全等.
ASA
AAS
(三角形内角和定理)
归纳总结 巩固新知
例题讲解
如图,AB与CD相交于点O,O是AB的中点,∠A=∠B,△AOC与△BOD全等吗?为什么?
A
B
C
D
O
解: △AOC≌△BOD.
在△AOC和△BOD中,
∴△AOC≌△BOD(ASA).
∠A =∠B,
AO = BO,
∠AOC =∠BOD,
理由如下: ∵O是AB的中点,
∴AO=BO
问题变式 思维拓展
变式一
A
B
C
D
O
A
B
C
D
E
F
如图∠A=∠B,∠AFC=∠BED,那么要得到△ACF≌△BDE,还应给出的条件是( )
A.∠C=∠D B.AC=ED
C.CF=BD D.AE=BF
注意:
要判定两个三角形全等时,边和角一定要“对应相等”,而不是“相等”.
D
∵AE=BF,
∴AE-EF=BF-EF
即 AF=BE
问题变式 思维拓展
变式二
A
B
C
D
O
A
B
C
D
E
F
提示:
如图AF=BE,AC∥BD,∠C=∠D,求证CF∥ED
由线平行可推出角相等,由角相等推出线平行.
∠A=∠B,
∠C =∠D,
AF= BE,
∴△ACF ≌△BDE(AAS).
∴∠AFC=∠BED
∴CF∥ED
证明:∵AC∥BD
∴∠A=∠B
在△ACF 和△BDE 中,
找条件,证全等
1.直接条件:
2.隐含条件:
3.间接条件:
A
B
C
D
E
F
∟
∟
归纳总结 巩固新知
即已知中直接给出的三角形的对应边或对应角.
即已知没有给出,但通过读图很容易得到的条件,
如公共边、公共角、对顶角等.
即已知中所给条件不是三角形的边和角,需要进一步推理.比如
平行、角平分线、垂直等都可得到角相等.中点、等式的基本性质
可推出线段相等等.
学以致用 思维提升
E
M
B
A
F
O
N
C
如图,O是线段EF的中点,∠E=∠F,∠A=∠B,
求证:△EOB≌△FOA
△AON≌△BOM
△ACM≌△BCN
AAS
ASA
AAS、ASA
证明两个三角形全等判定方法不一定是唯一的!根据条件选择合适的即可.
△EOM≌△FON
SSS、ASA、AAS
图中还有其他的全等三角形吗?请说明理由.
步步高
全等
全等
边、角相等
∵AO=BO,MO=NO
∴AO-MO=BO-NO
即 AM=BN
问题驱动 回扣情境
A
B
要保证做出的三角形与原来三角形全等,至少需要边或角的三个条件:
(2) 三条边
(1) 三个角
(3) 两角一边
SSS
不能!
(4) 两边一角
带B. 由“角边角”可知,利用这块能配出一个与原来全等的三角形玻璃.
ASA
AAS
课堂小结 反思提升
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”.
两角分别相等且其中一组等角的对边相等的两个三角形全等,简写成“角角边”或“AAS”.
探索三角形全等的条件
思想方法
要学会分类、转化等思想解决问题.
(SSS、ASA、AAS)
文化渗透 课外拓展
古人对全等三角形的认识源于测量.据史料记载.第一个应用全等三角形的人应该是古希腊学者泰勒斯(约公元前625一公元前547).他可谓是几何学的鼻祖,把演绎逻辑思想引入数学.尤其值得称道的是,他证明了第一个全等三角形的判定定理:也就是我们今天所研究的“角边角”定理.
有关全等三角形判定的历史追溯
古希腊数学家欧几里得试图利用较为严密的逻辑推理去推证全等的相关结论.“直觉是不可靠的”和“几何中无王者之路”是他的名言.欧几里得没有利用三角形内角和定理.而是分别对“等角夹边”和“等角对边”两种情况进行了证明,其中也应用了反证法. 有些数学家不满意欧几里得的证明.如阿拉伯数学家阿尔·奈里兹(865--922)在注释《原本》时,仍采用了叠置法.
文化渗透 课外拓展
有关全等三角形判定的历史追溯
对于同一个问题,数学家们虽然会有不同的见解.但在他们学术个性的背后仍存有共性,即甘于寂寞、坚韧不拔潜心钻研的精神值得我们学习.
在这特殊的阶段,相信同学们也会耐得住寂寞,不断学习,用知识缝制铠甲,不远的将来,当你们走向社会,各行各业都将由你们披甲上阵.加油!
新课引入
我们讨论这种情形:如果两个三角形有两条边和一个角分别对应相等,
那么这两个三角形一定全等吗?又有几种情况呢?
温馨提示
不重不漏哦!
两条边及其中一边的对角
两条边及两边的夹角(两边夹角)
探究体验
画一个三角形,两条边分别为2.5cm,3.5cm ,它们所夹的角为40 °
1.画一线段AB,使它等于3.5cm ;
2.画∠MAB = 40°;
3.在射线AM上截取AC =2.5cm ;
4.连结BC.
△ABC 就是所求的三角形.
A
B
M
C
.
3.5cm
.
.
2.5cm
.
.
实践检验
你画的三角形与同伴画的一定全等吗?
实践检验
A
B
C
A’
B’
C’
结论:
在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等.
真真假假
以2.5厘米、3.5厘米为三角形的两边,长度2.5厘米的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?
步骤:1.画一线段AC ,使它等于3.5厘米;
2.画∠CAM = 45°;
3.以C 为圆心, 2.5厘米长为半径画弧,
交AM 于点B.
4.连结CB.
△AB1 C 与△AB2 C 都符合所
要求作的三角形.
结论:两边及其一边所对的角相等,两个三角形无法确定全等.
C
A
B1
B2
.
M
3.5厘米
2.5厘米
2.5厘米
归纳结论
在两个三角形中,如果有两条边及它们的夹角对应
相等,那么这两个三角形全等,简记为SAS.
A
B
C
A’
B’
C’
几何语言
∵ AC = A’C’
∠A = ∠A’
AB = A’B’
∴ △ABC≌△A’B’C’ (SAS )
牛刀小试
在下列图中找出全等三角形,并把它们用直线连起来.
30?
8 cm
9 cm
30?
8 cm
8 cm
30?
8 cm
5 cm
8 cm
5 cm
30?
Ⅲ
30?
8 cm
8 cm
8 cm
5 cm
30?
5 cm
8 cm
Ⅳ
8 cm
9 cm
例题讲解
例1:如图,已知AB =AD,AC =AE,∠BAC =∠DAE,
说明△BAC 与△DAE 全等的理由.
AB =AD(已知)
∠BAC =∠DAE(已知)
AC =AE(已知)
∴△BAC≌△DAE(SAS)
A
D
E
在△ BAC 与△ DAE 中,
说明:
B
C
B
C
例2:如图,AB =AC,BE =CD.
试说明.
(1)△ABD ≌△ACE
(2)BD =CE
(3)∠B =∠C
例题讲解
B
C
A
D
E
AB =AC(已知)
∠A =∠A(公共角)
AD =AE(已证)
∴△ABD≌△ACE(SAS)
在△ABD 与△ACE 中,
(1)
∵ AB =AC,BE =CD
∴ AB –BE =AC-CD
即 AE =AD
(2)
∵ △ABD≌△ACE(已证)
∴BD =CE(全等三角形的对应边相等)
(3)∵ △ABD≌△ACE(已证)
∴∠B =∠C
说明
变式训练
1.如图,已知AB =AD,AC =AE, ∠BAD =∠CAE,
说明△BAC 与△DAE 全等的理由.
A
B
C
D
E
说明:
∵ ∠BAD =∠CAE
∴ ∠BAD -∠CAD =∠CAE -∠CAD
∴ ∠BAC =∠DAE
在△BAC 与△DAE 中,
AB =AD(已知)
∠BAC =∠DAE(已证)
AC =AE(已知)
∴△BAC ≌△ DAE (SAS)
2 .如图,已知AB =DC,∠ABC =∠DCB,那么△ABC 与△DCB
是否全等?为什么?
变式训练
A
B
D
C
△ABC 与△DCB 全等
说明:
在△ABC 与△DCB 中,
AB =DC(已知)
∠ABC =∠DCB (已知)
BC =CB(公共边)
∴△ABC≌△DCB (SAS)
3 . 如图,AB∥DE,
AB =DE,BE =CF
(1) BC =EF
(2)△ABC≌△DEF
(3)AC∥DF
变式训练
A
B
C
E
F
D
AB =DE(已知)
∠ABC =∠DEF (已证)
BC =EF(已证)
∴△ABC ≌△DEF(SAS)
在△ABC与△DEF中,
(1)说明:
∵ BE =CF
∴ BE +EC =CF +EC
∴ BC =EF
∵△ABC≌△DEF (已证)
(3)解:∵ △ ABD≌△ ACE(已证)
∴∠B=∠C(全等三角形的对应角相等)
(2)说明:
∵ AB∥DE
∴ ∠ABC =∠DEF
(3)说明
∴ ∠ACB =∠DFE(全等三角形的对应角相等)
∴ AC ∥ DF
试说明:
拓展提升
如图,已知AB =AE, ∠B =∠E, BC=ED,F是CD 的中点,试说明AF ⊥CD.
A
C
B
D
E
F
拓展提升
A
C
B
D
E
F
在△ABC 与△AED 中
AB = AE
∠B = ∠E
BC = ED
∴ △ABC ≌△AED (SAS)
在△ACF 与△ADF 中
AC =AD
AF = AF
CF =DF
∴ △ACF ≌△ADF (SSS)
∴ ∠AFC =∠AFD
又∵ F是CD 的中点
∴CF =DF
说明:连接AC,AD
∵ ∠AFC +∠AFD = 1800
∴ ∠AFC =∠AFD = 900
∴ AF ⊥CD
∴AC =AD
1.如图所示, 根据题目条件,判断下面的三角形是否全等.
(1) AC =DF, ∠C =∠F, BC =EF ;
课堂检测
A
E
D
F
C
B
能
能
A
B
C
D
(2) BC =BD, ∠ABC =∠ABD.
2.小明做了一个如图所示的风筝,其中∠EDH =∠FDH, ED =FD ,将上述
条件标注在图中,小明不用测量就能知道EH=FH吗?与同桌进行交流.
课堂检测
F
D
H
E
ED =FD
∠EDH =∠FDH(已知)
DH = DH(公共边)
∴△EDH ≌△FDH (SAS)
∴EH =FH(全等三角形对应边相等)
说明:在△EDH 和△FDH 中
3.如图,已知AB 和CD 相交与O, OA=OB, OC =OD.说明 AD ∥ BC.
课堂检测
O
A
B
C
D
1
2
说明:在△OAD 和△OBC中
OA = OB(已知)
∠1 = ∠2(对顶角相等)
OD = OC (已知)
∴△OAD ≌△OBC (SAS)
∴ ∠A = ∠B
∴ AD ∥ BC
学习收获
4、遇到较为复杂的图形时,可以采用图形分离法(将基本图形分离).
3、注意对应边和对应角的确定,特别是公共边和公共角的应用.
2、注意规范书写证明三角形全等的基本步骤.
1、新的一个三角形全等的判定方法:在两个三角形中,如果有两条边 及它们的夹角对应相等,那么这两个三角形全等(简记为SAS).
5、无法直接证明三角形全等时,考虑辅助线的添加.
学习收获
常用到的全等的基本图形
O
A
B
C
D
A
B
C
D
E
A
B
C
D
A
B
C
E
F
D
1.如图,点E 在AB上,AC =AD, ∠CAB =∠DAB , △ACE 与△DAE 全等吗?
课后作业
B
D
A
C
E
△ACB 与△ADB 呢? 请说明理由.
2.如图,已知AB =AD,AC =AE,BA⊥DA,AC⊥AE,
说明△BAC 与△DAE 全等的理由.
A
B
C
D
E
课后作业
3.小颖作业本上画的三角形被墨迹污染,她想画出一个与原来完全一样
的三角形,她该怎么办呢?请帮助小颖想出一个办法来,并说明理由.
课后作业
4.如图, △EFG 的三条边相等,三个内角也相等,且EH =FI =GJ,
△EHJ, △FIH, △GJI全等吗? △HIJ 的三边相等吗?
课后作业
E
I
H
J
G
F
提升题:
有一块三角形木板,如图,由于实际生产的需要,工人师傅要把∠MON
平分开,现在他手边只有一根细绳和一把直尺,你能帮助工人师傅想个
办法吗?并说明理由.
M
O
N
课后作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
