北师大版七年级数学下册 4.4用尺规作三角形课件(24ppt)
文档属性
| 名称 | 北师大版七年级数学下册 4.4用尺规作三角形课件(24ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 66.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 09:33:55 | ||
图片预览




文档简介
(共25张PPT)
用尺规作三角形
情境引入
如右图,小颖作业本上画的三角形被墨迹污染,她想用尺规作图的方法画一个与原来三角形完全一样的三角形,她该怎样做呢?
知识唤醒
尺规作图是起源于古希腊的数学课题,是指用无刻度的直尺和圆规作图。并且只准许使用有限次,来解决不同的平面几何作图题。
相传,是古希腊的数学家安那萨哥拉斯首先提出作图要有尺寸限制。他因政治上的纠葛,被关进监狱,并被判处死刑。在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间不多了,因此他很自然地想到要有限次地使用尺规解决问题。这就是尺规作图最早的来源,后来不断在古希腊流传,并以理论形式具体明确在欧几里德的《几何原本》中。因其作图工具的简洁和衍生问题之广,从古至今吸引着数学家和爱好者不断探索。
知识唤醒
已知:线段a,∠α,
求作:求作线段BC,∠A,使BC=a,∠A=∠α.
新课学习
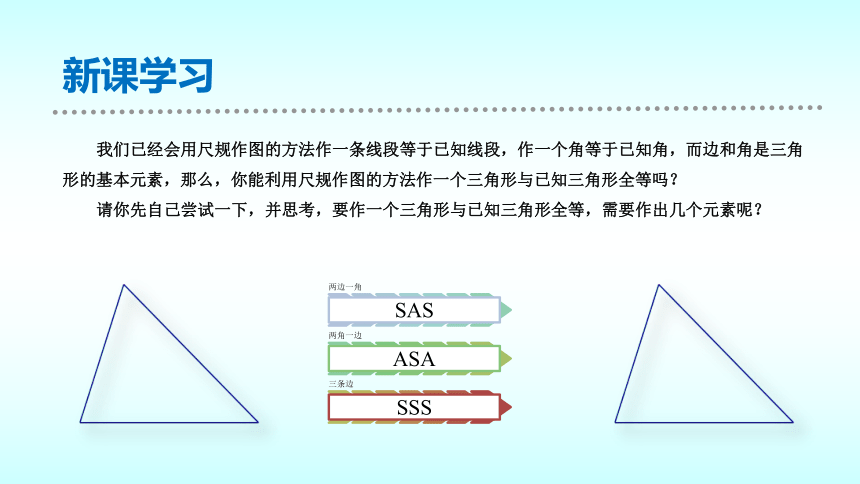
我们已经会用尺规作图的方法作一条线段等于已知线段,作一个角等于已知角,而边和角是三角形的基本元素,那么,你能利用尺规作图的方法作一个三角形与已知三角形全等吗?
请你先自己尝试一下,并思考,要作一个三角形与已知三角形全等,需要作出几个元素呢?
新课学习
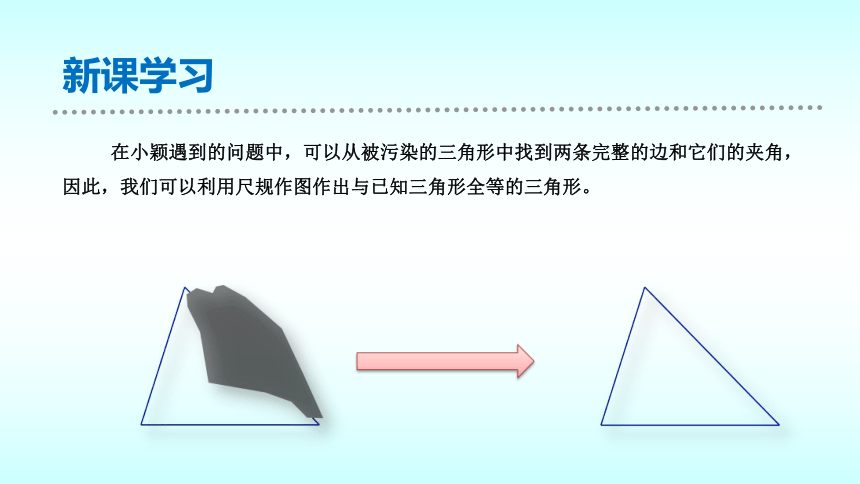
在小颖遇到的问题中,可以从被污染的三角形中找到两条完整的边和它们的夹角,因此,我们可以利用尺规作图作出与已知三角形全等的三角形。
新课学习
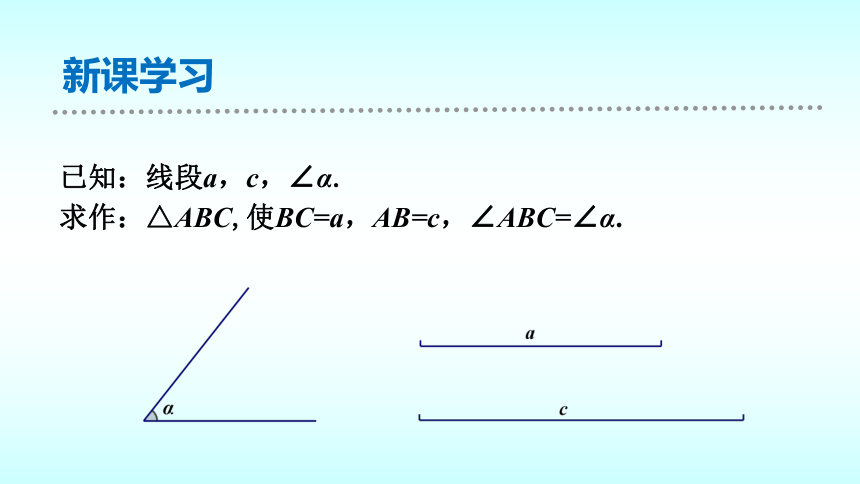
已知:线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
新课学习
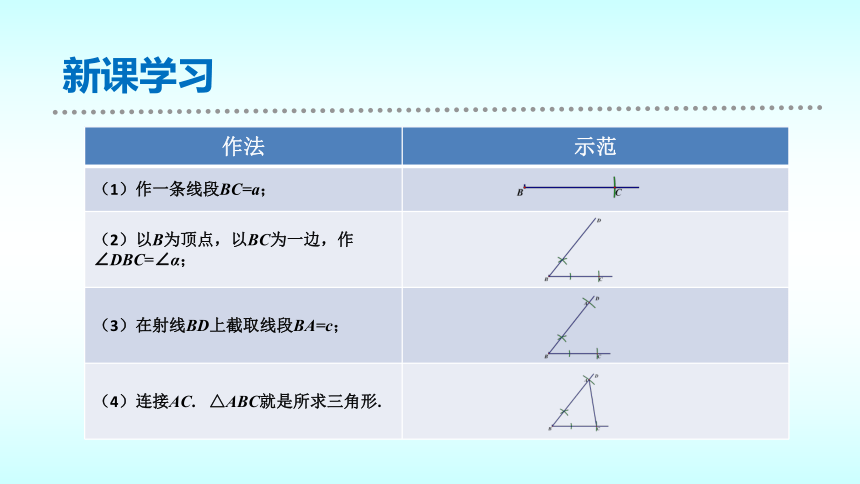
作法 示范
(1)作一条线段BC=a;
(2)以B为顶点,以BC为一边,作
∠DBC=∠α;
(3)在射线BD上截取线段BA=c;
(4)连接AC. △ABC就是所求三角形.
新课学习
已知:线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
新课学习
SAS
新课学习
已知:∠α,∠β,线段c.
求作:△ABC,使∠A=∠α,使∠B=∠β,AB=c.
新课学习
作法 图形
(1)作∠DAF=∠α;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,
作∠ABE=∠β,BE交AD于点C.
△ ABC 就是所求作的三角形.
新课学习
已知:∠α,∠β,线段c.
求作:△ABC,使∠A=∠α,使∠B=∠β,AB=c.
新课学习
已知:线段a,b,c.
求作:△ABC,使AB=c,AC=b,BC=a.
新课学习
作法 图形
(1)
(2)
……
新课学习
已知:线段a,b,c.
求作:△ABC,使AB=c,AC=b,BC=a.
巩固练习
已知∠α和线段a,用尺规作一个三角形,使其一个内角等于,另一个内角等于2∠α,且这两个内角的夹边等于a.
巩固练习
已知∠α和线段a,用尺规作一个三角形,使其一个内角等于,另一个内角等于2∠α,且这两个内角的夹边等于a.
巩固练习
2. 已知线段a,用尺规作△ABC ,使AB=a,BC=AC=2a.
巩固练习
颗粒归仓
数海拾贝
千百年来,有许许多多关于尺规作图的有趣例子,最为经典的要数大数学家高斯与正十七边形的尺规作图法。1796年的一天,德国哥廷根大学,高斯吃完晚饭,开始做导师给他单独布置的三道数学题。前两道题他不费吹灰之力就做了出来了,第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。这道题把他难住了——所学过的数学知识竟然对解出这道题没有任何帮助。时间一分一秒的过去了,第三道题竟毫无进展,他绞尽脑汁,尝试着用一些超常规的思路去寻求答案,当窗口露出曙光时,他终于解决了这道难题。
当他把作业交给导师时,感到很惭愧。他对导师说:“您给我布置的第三道题,我竟然做了整整一个通宵,……”可导师却激动地对他说:“你知不知道?你解开了一桩有两千多年历史的数学悬案!阿基米得没有解决,牛顿也没有解决,你竟然一个晚上就解出来了,你是一个真正的天才!”原来,导师也一直想解开这道难题,他是因为拿错了纸条,才将这道题目交给了高斯。
后来高斯曾回忆说:“如果有人告诉我,那是一道千古难题,我可能永远也没有信心将它解出来。”
数海拾贝
还有一些很美丽的图案,也可以用尺规作图非常完美的作出,同学们,请你试着用尺规作图的方法作出下面的图案吧!
数海拾贝
由于尺规作图对作图工具的限制,使得一些貌似简单的几何作图问题却始终无法解决。最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题。当时很多有名的希腊数学家都曾着力于研究这三大问题,却一直未能如愿以偿。以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终。直到1637年笛卡儿创立了解析几何,关于尺规作图的可能性问题才有了准则。到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题,1882年林德曼证明了π是超越数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案。
虽然几何三大问题不能用尺规作图解决,但在研究过程中得到了大量价值非凡的副产品,特别是开创了对圆锥曲线的研究,发现了一批著名的曲线等。不仅如此,三大问题还和近代的方程论、群论等数学分支发生了关系。
数海拾贝
《孟子》卷四中说“不以规矩,不能成方圆”;古代先贤以“尺规”的比喻来告诫我们,做任何事情都要循规律,知边界,守法度。
愿大家心存尺墨,行有规节,不断勾画出幸福充盈,精彩纷呈的人生图案。
用尺规作三角形
情境引入
如右图,小颖作业本上画的三角形被墨迹污染,她想用尺规作图的方法画一个与原来三角形完全一样的三角形,她该怎样做呢?
知识唤醒
尺规作图是起源于古希腊的数学课题,是指用无刻度的直尺和圆规作图。并且只准许使用有限次,来解决不同的平面几何作图题。
相传,是古希腊的数学家安那萨哥拉斯首先提出作图要有尺寸限制。他因政治上的纠葛,被关进监狱,并被判处死刑。在监狱里,他思考改圆成方以及其他有关问题,用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具,只能用一根绳子画圆,用随便找来的破木棍作直尺,当然这些尺子上不可能有刻度.另外,对他来说,时间不多了,因此他很自然地想到要有限次地使用尺规解决问题。这就是尺规作图最早的来源,后来不断在古希腊流传,并以理论形式具体明确在欧几里德的《几何原本》中。因其作图工具的简洁和衍生问题之广,从古至今吸引着数学家和爱好者不断探索。
知识唤醒
已知:线段a,∠α,
求作:求作线段BC,∠A,使BC=a,∠A=∠α.
新课学习
我们已经会用尺规作图的方法作一条线段等于已知线段,作一个角等于已知角,而边和角是三角形的基本元素,那么,你能利用尺规作图的方法作一个三角形与已知三角形全等吗?
请你先自己尝试一下,并思考,要作一个三角形与已知三角形全等,需要作出几个元素呢?
新课学习
在小颖遇到的问题中,可以从被污染的三角形中找到两条完整的边和它们的夹角,因此,我们可以利用尺规作图作出与已知三角形全等的三角形。
新课学习
已知:线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
新课学习
作法 示范
(1)作一条线段BC=a;
(2)以B为顶点,以BC为一边,作
∠DBC=∠α;
(3)在射线BD上截取线段BA=c;
(4)连接AC. △ABC就是所求三角形.
新课学习
已知:线段a,c,∠α.
求作:△ABC,使BC=a,AB=c,∠ABC=∠α.
新课学习
SAS
新课学习
已知:∠α,∠β,线段c.
求作:△ABC,使∠A=∠α,使∠B=∠β,AB=c.
新课学习
作法 图形
(1)作∠DAF=∠α;
(2)在射线AF上截取线段AB=c;
(3)以B为顶点,以BA为一边,
作∠ABE=∠β,BE交AD于点C.
△ ABC 就是所求作的三角形.
新课学习
已知:∠α,∠β,线段c.
求作:△ABC,使∠A=∠α,使∠B=∠β,AB=c.
新课学习
已知:线段a,b,c.
求作:△ABC,使AB=c,AC=b,BC=a.
新课学习
作法 图形
(1)
(2)
……
新课学习
已知:线段a,b,c.
求作:△ABC,使AB=c,AC=b,BC=a.
巩固练习
已知∠α和线段a,用尺规作一个三角形,使其一个内角等于,另一个内角等于2∠α,且这两个内角的夹边等于a.
巩固练习
已知∠α和线段a,用尺规作一个三角形,使其一个内角等于,另一个内角等于2∠α,且这两个内角的夹边等于a.
巩固练习
2. 已知线段a,用尺规作△ABC ,使AB=a,BC=AC=2a.
巩固练习
颗粒归仓
数海拾贝
千百年来,有许许多多关于尺规作图的有趣例子,最为经典的要数大数学家高斯与正十七边形的尺规作图法。1796年的一天,德国哥廷根大学,高斯吃完晚饭,开始做导师给他单独布置的三道数学题。前两道题他不费吹灰之力就做了出来了,第三道题写在另一张小纸条上:要求只用圆规和没有刻度的直尺,作出一个正十七边形。这道题把他难住了——所学过的数学知识竟然对解出这道题没有任何帮助。时间一分一秒的过去了,第三道题竟毫无进展,他绞尽脑汁,尝试着用一些超常规的思路去寻求答案,当窗口露出曙光时,他终于解决了这道难题。
当他把作业交给导师时,感到很惭愧。他对导师说:“您给我布置的第三道题,我竟然做了整整一个通宵,……”可导师却激动地对他说:“你知不知道?你解开了一桩有两千多年历史的数学悬案!阿基米得没有解决,牛顿也没有解决,你竟然一个晚上就解出来了,你是一个真正的天才!”原来,导师也一直想解开这道难题,他是因为拿错了纸条,才将这道题目交给了高斯。
后来高斯曾回忆说:“如果有人告诉我,那是一道千古难题,我可能永远也没有信心将它解出来。”
数海拾贝
还有一些很美丽的图案,也可以用尺规作图非常完美的作出,同学们,请你试着用尺规作图的方法作出下面的图案吧!
数海拾贝
由于尺规作图对作图工具的限制,使得一些貌似简单的几何作图问题却始终无法解决。最著名的是被称为几何三大问题的三个古希腊古典作图难题:立方倍积问题、三等分任意角问题和化圆为方问题。当时很多有名的希腊数学家都曾着力于研究这三大问题,却一直未能如愿以偿。以后两千年来,无数数学家为之绞尽脑汁,都以失败而告终。直到1637年笛卡儿创立了解析几何,关于尺规作图的可能性问题才有了准则。到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题,1882年林德曼证明了π是超越数,化圆为方问题不可能用尺规作图解决,这才结束了历时两千年的数学难题公案。
虽然几何三大问题不能用尺规作图解决,但在研究过程中得到了大量价值非凡的副产品,特别是开创了对圆锥曲线的研究,发现了一批著名的曲线等。不仅如此,三大问题还和近代的方程论、群论等数学分支发生了关系。
数海拾贝
《孟子》卷四中说“不以规矩,不能成方圆”;古代先贤以“尺规”的比喻来告诫我们,做任何事情都要循规律,知边界,守法度。
愿大家心存尺墨,行有规节,不断勾画出幸福充盈,精彩纷呈的人生图案。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
