四年级下册数学教案-数学广角-鸡兔同笼 -人教版
文档属性
| 名称 | 四年级下册数学教案-数学广角-鸡兔同笼 -人教版 |

|
|
| 格式 | zip | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览



文档简介
《数学广角——鸡兔同笼》教学设计
江西省铜鼓县第二小学
教学内容
教育部审定2011义务教育教科书四年级下册数学《数学广角——鸡兔同笼》
二、教学目标
1、了解“鸡兔同笼”问题的结构特点,尝试用列表、画图、假设等策略解决“鸡兔同笼”问题。
2、在解决问题的过程中,培养学生的思维能力,并向学生渗透化繁为简、假设的数学思想和方法,经历数学思想具体化的过程,构建数学模型。
3、在学习过程中,感受古代数学问题的趣味性,体会“鸡兔同笼”问题在生活中的广泛应用,提高学习数学的兴趣。
三、教学重点:运用假设法构建“鸡兔同笼”问题的数学模型,并应用模型解决问题。
四、教学难点:让学生区分出运用假设法构建的“鸡兔同笼”问题的数学模型中表示鸡与兔的算式。
五、教学准备:教师准备多媒体课件,学生准备空表格和可擦笔一支。
(设计意图:这节课所采用的“列表法”“画图法”实际上是假设法的一种。因为假设这种思想方法对学生来说具有一定的思维难度,不能被所有学生所理解和掌握,因此在这里借助画图把假设的对象具体化、形象化,就要借助可擦笔演绎假设、推理的过程,让学生在用模的过程中逐渐体会假设法的内涵。)
教学设计
明确任务,引入新课。
今天刘老师想带你们进入这3块园地学习数学知识,有兴趣吗?(电脑展示鸡兔同笼园——龟鹤同游园——鸡兔同戏园)(生:有!)出发!进入——鸡兔同笼园
师:相传在1500多年前,鸡兔关在一个笼子里,相处得非常和睦。我们今天学习的就是——板书课题(鸡兔同笼问题)
【设计意图:以3块园地的导图引入新课,使学习材料变得非常有挑战性和趣味性。】
进入鸡兔同笼园,初步建立数学模型。
(一)了解古题,简化数据。
师:在1500多年前的《孙子算经》中就记载了这样一道鸡兔同笼问题,让我们翻开这本书去了解一下这道古题——(音画展开原题)
今有雉兔同笼,上有三十五足,下有九十四足,问雉兔各几何?
师:雉是野鸡的意思,谁来说说短短的4句话是什么意思?(指名说意思)
师:看来你的语文功底很扎实,真的是——(屏幕出示正确意思)
师:你会算吗?(指名回答)
师: 你呢?(指另一名回答)
师: 你们会算吗?(让全班回答)
师:老师也挺为难,是呀,35只鸡兔的头,即便我们画完了,也没有时间解决问题呀。老师给你们一个建议,把数据进行简化,行吗?(电脑出示简化后的题,学生读题):
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数有26条腿。
鸡和兔各有几只?
【设计意图:古题做成音画,使学生感悟数学文化的源远流长;古题数据太大,简化数据,渗透着化繁为简的思想,尊重学生知识接受基础。】
(二)寻求规律,内化解法
1.理清题意。
师:题目中提供了几条重要的数学信息?你还能挖掘出其它的数学信息吗?
(借助表格简单理解)
思考猜想
师:“没有大胆的猜想就没有伟大的发现。”你也可以猜猜,说不定会有惊喜呢。
师: 你可能不能一下子找到答案,但我们可以——(学生说)先根据什么条件猜?你试一试——,正确否,还要根据什么条件继续猜?直到——。
生猜测,师根据学生猜测,随机填如下表,逐步验证。
鸡
兔
腿
3.完善表格。
师:孩子们经过多次尝试找寻到鸡有3只,兔有5只,向你们表示祝贺。为了使我们的研究更有参考价值,应该尽可能考虑到每一种情况。(指名让学生继续完善、补充表格)
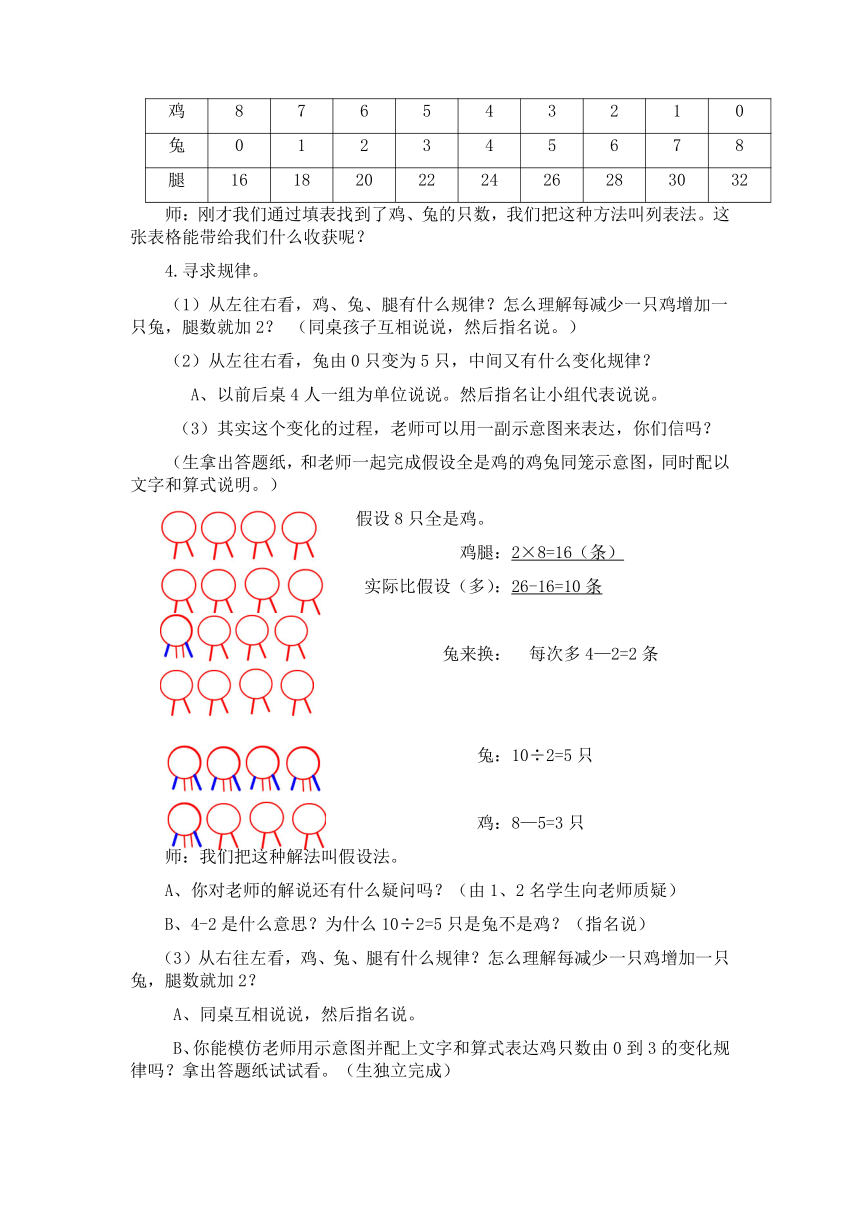
鸡 8 7 6 5 4 3 2 1 0
兔 0 1 2 3 4 5 6 7 8
腿 16 18 20 22 24 26 28 30 32
师:刚才我们通过填表找到了鸡、兔的只数,我们把这种方法叫列表法。这张表格能带给我们什么收获呢?
4.寻求规律。
从左往右看,鸡、兔、腿有什么规律?怎么理解每减少一只鸡增加一只兔,腿数就加2? (同桌孩子互相说说,然后指名说。)
从左往右看,兔由0只变为5只,中间又有什么变化规律?
A、以前后桌4人一组为单位说说。然后指名让小组代表说说。
(3)其实这个变化的过程,老师可以用一副示意图来表达,你们信吗?
(生拿出答题纸,和老师一起完成假设全是鸡的鸡兔同笼示意图,同时配以文字和算式说明。)
假设8只全是鸡。
鸡腿:2×8=16(条)
实际比假设(多):26-16=10条
兔来换: 每次多4—2=2条
兔:10÷2=5只
鸡:8—5=3只
师:我们把这种解法叫假设法。
你对老师的解说还有什么疑问吗?(由1、2名学生向老师质疑)
4-2是什么意思?为什么10÷2=5只是兔不是鸡?(指名说)
(3)从右往左看,鸡、兔、腿有什么规律?怎么理解每减少一只鸡增加一只兔,腿数就加2?
A、同桌互相说说,然后指名说。
B、你能模仿老师用示意图并配上文字和算式表达鸡只数由0到3的变化规律吗?拿出答题纸试试看。(生独立完成)
C、哪位孩子来做一名小老师向同学们讲解假设全是兔的解法?(指名上台讲解。)
D、对他的讲解满意吗?还有什么问题要问他吗?
(3)比照两种假设方法,找到求鸡、兔只数的秘诀。
小结方法,比较优劣。
师:我们学会了用哪些方法解鸡兔同笼问题?你会选择哪种方法?为什么?
【设计意图:猜测、列表尝试法,是解决问题的一种重要的策略和方法。但当问题中的数据比较大的时候,列表的方法就会很繁琐、复杂,这时教师充分利用学生的列表资源,引导学生从表格中寻找鸡、兔、脚的规律,并把规律分别用图形表达,生动地演绎假设法的解答过程,从而也可以体验不同方法间的内在联系。给示意图配以文字和算式,图文并茂,形象直观,有利于学生在思考、操作中内化假设法解鸡兔同笼问题。】
(三)今解古题,深化解法
师:我很想用假设法解决《孙子算经》中的鸡兔同笼古题,你们能帮老师度过这个难关吗?
师提醒:这里数字大,如需画图可以采用联想法,画一半,留一半在心里想像出画。
生独立解答。
假设全是鸡(由一名代表汇报解法并生解答伊始,
A、生在答题纸上独立完成(解答伊始播放古筝曲《高山流水》60秒)
B、选一名学生汇报解法,其他学生如有疑问要释疑。
假设全是兔
A、生在答题纸上独立完成(解答伊始播放古筝曲《渔舟唱晚》60秒)
B、选一名学生汇报解法,其他学生如有疑问要释疑。
2.再次比较,体会假设法的简洁、明快。
(三)适当评价,结束第一园学习
师:鸡兔同笼园的学习就要结束了,这一站谁是最佳学员?(生评师鼓励)
【设计意图:音乐是一种熏陶,在轻快短暂的音乐中催发学生解题的思维兴奋度;独学是一种能力,汇报是一种分享,评价是为了促进下一环节的学习。在愉悦的学习氛围中,初步建立了鸡兔同笼的数学模型。】
三、进入龟鹤同游园,巩固数学模型
(一)引入龟鹤同游园
师: 鸡兔同笼问题传到日本就变成了龟鹤同游问题,接下来进入龟鹤同游园学习。这个园子里有龟鹤——(电脑出示题目:有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?)
(二)建立联系
请仔细看题,这里鸡、兔总头数看成多少?总腿数呢?谁当作鸡?谁又当成兔呢?你有信心解答吗?
独立解答(生解答伊始,播放轻音乐《仙鹤情缘》60秒)
师:请孩子们答题纸上完成这道题。
展示评价
1.展示汇报(指名让学生带答题纸到台前对自己的解法发表解说)
2.评价激励。
师:龟鹤同游园学习很快就结束了,祝贺以上孩子成为最佳学员。
【设计意图:给学生提供独立解决问题的时间,使学生熟练用假设法解决鸡兔同笼问题,巩固鸡兔同笼的数学模型,培养应用数学模型解决问题的能力。】
四、进入鸡兔同戏园,演绎抬足法
师:鸡兔同笼问题被我们用假设法破解了,你能用两个字描绘一下你此刻的心情吗?(生:开心、快乐、高兴......)是呀,老师也为你们感到骄傲。假设法有多种思路,除了假设笼子里全是鸡或者全是兔的方法外,“抬足法”也是假设法的一种。现在我们一起进入鸡兔同戏园做“抬足法”游戏吧。
电脑出示游戏规则:我们班61位孩子。把鸡、兔总头数当作61,事先不知自己是鸡还是兔。老师报出总腿数后。听老师指挥,吹第一声口哨,抬左腿;吹第二声口哨,再抬右腿。最后算出鸡、兔各几只?
师报出总腿数为172,开始玩第一次游戏。
师:全体起立(吹第一声口哨,生抬起左腿。)
师:还有多少条腿?(生:172-61=111条)
师吹第二声口哨后笑问:为什么都坐下了?(生:因为没有腿可抬了。)
师:现在还有多少条腿?(生:111-61=50条)
师:剩下的腿是谁的腿?(生:兔子的。)
师:每只兔子还剩下几条腿?(2条)
师:有几只兔子?(50÷2=25只)
师:鸡呢?(生:61-25=36只)
师报出总腿数为162,开始玩第二次游戏。
3. 师:我们又学会了一种解决鸡兔同笼问题的方法,老师给这种方法起个名字——“抬足法”。“抬足法”的形式有多种。试想,兔子和鸡都抬起一半的脚,会怎样呢?这个游戏,孩子们可以课后接着玩。把你所玩的收获写成一篇数学日记交给老师,行吗?
【设计意图:假设法有多种思路,除了假设笼子里全是鸡或者全是兔的方法外,“抬足法”也是假设法的一种。用游戏的方式演绎“抬足法”,使学习资源变得鲜活有趣。“试想,兔子和鸡都抬起一半的脚,会怎样呢?这个游戏,孩子们可以课后接着玩。”以这样的言语激励学生大胆尝试,把鸡兔同笼问题的解决办法进一步拓展。】
畅谈收获,引向纵深。
今天我们解决了一个什么问题?你有什么收获?(选2、3名学生说说)
生1:我学会了用列表法、假设法和抬足法解决鸡兔同笼问题。
师:你的收获真多。
生2:我喜欢用假设法解鸡兔同笼问题,因为假设法解题清楚、明了。
师:很有思想。
生3:我喜欢用抬足法解题,因为抬足法有趣、好玩。
师:有见地。
师:我相信,只要孩子们大胆尝试、积极探究,一定能找到更多、更妙的解决鸡兔同笼问题的方法。
全课教学反思
“鸡兔同笼”问题是我国古代著名的数学趣题,最早出现在《孙子算经》中。解决这类问题有两类方法,一类是“假设法”,古代民间一般是这种方法,另一类是方程解法。“鸡兔同笼”问题在不同版本的教材中都有安排,在人教版2011教材中,这一知识安排在四年级下册数学广角中。教材先说明“鸡兔同笼”问题是我国古代著名的数学问题,再由生动有趣的古代课堂情境引出“鸡兔同笼”原题,并对原题给予解释,由小精灵提出“这个问题你能解决吗”,学生冥思苦想的画面激发学生解决该类问题的兴趣。由于“鸡兔同笼”原题的数据较大,不便于学生进行探究,所以教材以化繁为简的思想为指导,先在例1中安排一道数据较小的“鸡兔同笼”问题让学生探索解决的方法。教材首先呈现了学生最“朴素”的想法——猜测。先猜测鸡、兔各有几只,然后验证脚的只数是否符合条件,如果不对,再猜,这样有时也能找到答案,但有一定的盲目性。下面的表格用来帮助学生按顺序寻找答案,但当数据太大时,不是很合适。这时小精灵提出:还有其他方法吗?让学生去探究更具有逻辑性的解法。教材中主要呈现了“假设法”。回想这堂课,主要有如下体会:
一、尊重学生知识起点,渗透两个思想。
1.渗透化繁为简思想,体会数学的简洁美。
当把《孙子算经》中鸡兔同笼的原题展现在学生面前时,我问:谁会解这道题?学生呈现给我一副苦思瞑想的神态,我及时点拨:为了研究方便,我们可以把数字简化。
当学生用折中列表法和跳跃列表法找到正确答案后,我及时引起学生思考:你所填的鸡、兔、腿数有什么规律?让我们继续完善这张表再观察:鸡、兔、腿的规律。当学生一致统一看法后,我引导学生用两副示意图分别表达假设全是鸡和全是兔的推导过程并配以简洁的文字和算式表述推理。
2.渗透假设法思想,理会解题的内涵。
当学生列表找到鸡、兔、腿的规律后,我适时引导学生把规律转化成一种切实可行的能马上找到答案的方法——假设法。借助图形,学生深刻领悟了假设法的推理过程,减少了差错。用抬足法游戏解题,打开了学生的思路。
恰当运用多媒体,体现多媒体的课堂价值。
古题做成音画,让古朴纯厚的数学气息弥漫于数学课堂。
练习过程中,穿插轻音乐,减少学生练习的疲劳感。
三、多角度提供思考、展示的空间,扎实掌握所学知识。
1.提供思考支点,使学生在思考中完善、验证。在新课教学活动中,当学生理解了题目意思后,我引导学生思考:你可能不能一下子找到答案,但我们可以——先根据什么条件猜?正确与否,还要根据什么条件继续猜?直到——。这样,学生在填表时就会有的放矢。
2.操作中引导思考,使学生内化知识。在教学用假设法解决例题中的鸡兔同笼问题时,我引导学生借助图形边画边思考,并把这种思考和画图的过程转化成文字和算式,内化了鸡兔同笼问题的知识,建立了数学模型。
3.尊重学生思维,为学生提供展示、交流的机会。教学过程中,充分尊重学生的思维,提供给学生充裕的展示、交流的机会,如例题中的表格的完善来自于多名学生的表格填写数据,新课教学中第二副示意图和思维过程的表达是由一名学生充当小老师进行讲解,再由学生质疑、释疑、评价。在推广应用中,我把话语权交给学生,由学生表达解题的全过程,让学生享受到解题的乐趣。
四、多种形式开展合作学习,感受学习数学的乐趣。
1.表格的填写由多名学生猜想、调整、完善。
2.表格的规律采取同桌说一说,4人一小组组织说,代表展示说等形式分享学习成果和快乐。
3.借助游戏演绎“抬足法”。课尾,我组织学生在哨声中演绎“抬足法”,在欢快和谐的气氛中把课推向高潮。
五、发挥生生间、师生间的评价功能。
1.展示汇报中进行评价。学生每上台展示一次小组的成果都让学生来质疑评价“小老师”的表现。
2.学习园地中进行评价。每一次学习园地的学习活动结束时进行评价。
整堂课,依托三块学习原地,本着用多种形式建立“假设法”解决鸡兔同笼的数学模型、多种学习方式内化数学知识、多种渠道拓宽学生的解题思路、多角度引领数学思考的教学原则,使学生在乐中学,趣中学,玩中学。
江西省铜鼓县第二小学
教学内容
教育部审定2011义务教育教科书四年级下册数学《数学广角——鸡兔同笼》
二、教学目标
1、了解“鸡兔同笼”问题的结构特点,尝试用列表、画图、假设等策略解决“鸡兔同笼”问题。
2、在解决问题的过程中,培养学生的思维能力,并向学生渗透化繁为简、假设的数学思想和方法,经历数学思想具体化的过程,构建数学模型。
3、在学习过程中,感受古代数学问题的趣味性,体会“鸡兔同笼”问题在生活中的广泛应用,提高学习数学的兴趣。
三、教学重点:运用假设法构建“鸡兔同笼”问题的数学模型,并应用模型解决问题。
四、教学难点:让学生区分出运用假设法构建的“鸡兔同笼”问题的数学模型中表示鸡与兔的算式。
五、教学准备:教师准备多媒体课件,学生准备空表格和可擦笔一支。
(设计意图:这节课所采用的“列表法”“画图法”实际上是假设法的一种。因为假设这种思想方法对学生来说具有一定的思维难度,不能被所有学生所理解和掌握,因此在这里借助画图把假设的对象具体化、形象化,就要借助可擦笔演绎假设、推理的过程,让学生在用模的过程中逐渐体会假设法的内涵。)
教学设计
明确任务,引入新课。
今天刘老师想带你们进入这3块园地学习数学知识,有兴趣吗?(电脑展示鸡兔同笼园——龟鹤同游园——鸡兔同戏园)(生:有!)出发!进入——鸡兔同笼园
师:相传在1500多年前,鸡兔关在一个笼子里,相处得非常和睦。我们今天学习的就是——板书课题(鸡兔同笼问题)
【设计意图:以3块园地的导图引入新课,使学习材料变得非常有挑战性和趣味性。】
进入鸡兔同笼园,初步建立数学模型。
(一)了解古题,简化数据。
师:在1500多年前的《孙子算经》中就记载了这样一道鸡兔同笼问题,让我们翻开这本书去了解一下这道古题——(音画展开原题)
今有雉兔同笼,上有三十五足,下有九十四足,问雉兔各几何?
师:雉是野鸡的意思,谁来说说短短的4句话是什么意思?(指名说意思)
师:看来你的语文功底很扎实,真的是——(屏幕出示正确意思)
师:你会算吗?(指名回答)
师: 你呢?(指另一名回答)
师: 你们会算吗?(让全班回答)
师:老师也挺为难,是呀,35只鸡兔的头,即便我们画完了,也没有时间解决问题呀。老师给你们一个建议,把数据进行简化,行吗?(电脑出示简化后的题,学生读题):
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数有26条腿。
鸡和兔各有几只?
【设计意图:古题做成音画,使学生感悟数学文化的源远流长;古题数据太大,简化数据,渗透着化繁为简的思想,尊重学生知识接受基础。】
(二)寻求规律,内化解法
1.理清题意。
师:题目中提供了几条重要的数学信息?你还能挖掘出其它的数学信息吗?
(借助表格简单理解)
思考猜想
师:“没有大胆的猜想就没有伟大的发现。”你也可以猜猜,说不定会有惊喜呢。
师: 你可能不能一下子找到答案,但我们可以——(学生说)先根据什么条件猜?你试一试——,正确否,还要根据什么条件继续猜?直到——。
生猜测,师根据学生猜测,随机填如下表,逐步验证。
鸡
兔
腿
3.完善表格。
师:孩子们经过多次尝试找寻到鸡有3只,兔有5只,向你们表示祝贺。为了使我们的研究更有参考价值,应该尽可能考虑到每一种情况。(指名让学生继续完善、补充表格)
鸡 8 7 6 5 4 3 2 1 0
兔 0 1 2 3 4 5 6 7 8
腿 16 18 20 22 24 26 28 30 32
师:刚才我们通过填表找到了鸡、兔的只数,我们把这种方法叫列表法。这张表格能带给我们什么收获呢?
4.寻求规律。
从左往右看,鸡、兔、腿有什么规律?怎么理解每减少一只鸡增加一只兔,腿数就加2? (同桌孩子互相说说,然后指名说。)
从左往右看,兔由0只变为5只,中间又有什么变化规律?
A、以前后桌4人一组为单位说说。然后指名让小组代表说说。
(3)其实这个变化的过程,老师可以用一副示意图来表达,你们信吗?
(生拿出答题纸,和老师一起完成假设全是鸡的鸡兔同笼示意图,同时配以文字和算式说明。)
假设8只全是鸡。
鸡腿:2×8=16(条)
实际比假设(多):26-16=10条
兔来换: 每次多4—2=2条
兔:10÷2=5只
鸡:8—5=3只
师:我们把这种解法叫假设法。
你对老师的解说还有什么疑问吗?(由1、2名学生向老师质疑)
4-2是什么意思?为什么10÷2=5只是兔不是鸡?(指名说)
(3)从右往左看,鸡、兔、腿有什么规律?怎么理解每减少一只鸡增加一只兔,腿数就加2?
A、同桌互相说说,然后指名说。
B、你能模仿老师用示意图并配上文字和算式表达鸡只数由0到3的变化规律吗?拿出答题纸试试看。(生独立完成)
C、哪位孩子来做一名小老师向同学们讲解假设全是兔的解法?(指名上台讲解。)
D、对他的讲解满意吗?还有什么问题要问他吗?
(3)比照两种假设方法,找到求鸡、兔只数的秘诀。
小结方法,比较优劣。
师:我们学会了用哪些方法解鸡兔同笼问题?你会选择哪种方法?为什么?
【设计意图:猜测、列表尝试法,是解决问题的一种重要的策略和方法。但当问题中的数据比较大的时候,列表的方法就会很繁琐、复杂,这时教师充分利用学生的列表资源,引导学生从表格中寻找鸡、兔、脚的规律,并把规律分别用图形表达,生动地演绎假设法的解答过程,从而也可以体验不同方法间的内在联系。给示意图配以文字和算式,图文并茂,形象直观,有利于学生在思考、操作中内化假设法解鸡兔同笼问题。】
(三)今解古题,深化解法
师:我很想用假设法解决《孙子算经》中的鸡兔同笼古题,你们能帮老师度过这个难关吗?
师提醒:这里数字大,如需画图可以采用联想法,画一半,留一半在心里想像出画。
生独立解答。
假设全是鸡(由一名代表汇报解法并生解答伊始,
A、生在答题纸上独立完成(解答伊始播放古筝曲《高山流水》60秒)
B、选一名学生汇报解法,其他学生如有疑问要释疑。
假设全是兔
A、生在答题纸上独立完成(解答伊始播放古筝曲《渔舟唱晚》60秒)
B、选一名学生汇报解法,其他学生如有疑问要释疑。
2.再次比较,体会假设法的简洁、明快。
(三)适当评价,结束第一园学习
师:鸡兔同笼园的学习就要结束了,这一站谁是最佳学员?(生评师鼓励)
【设计意图:音乐是一种熏陶,在轻快短暂的音乐中催发学生解题的思维兴奋度;独学是一种能力,汇报是一种分享,评价是为了促进下一环节的学习。在愉悦的学习氛围中,初步建立了鸡兔同笼的数学模型。】
三、进入龟鹤同游园,巩固数学模型
(一)引入龟鹤同游园
师: 鸡兔同笼问题传到日本就变成了龟鹤同游问题,接下来进入龟鹤同游园学习。这个园子里有龟鹤——(电脑出示题目:有龟和鹤共40只,龟的腿和鹤的腿共有112条。龟、鹤各有几只?)
(二)建立联系
请仔细看题,这里鸡、兔总头数看成多少?总腿数呢?谁当作鸡?谁又当成兔呢?你有信心解答吗?
独立解答(生解答伊始,播放轻音乐《仙鹤情缘》60秒)
师:请孩子们答题纸上完成这道题。
展示评价
1.展示汇报(指名让学生带答题纸到台前对自己的解法发表解说)
2.评价激励。
师:龟鹤同游园学习很快就结束了,祝贺以上孩子成为最佳学员。
【设计意图:给学生提供独立解决问题的时间,使学生熟练用假设法解决鸡兔同笼问题,巩固鸡兔同笼的数学模型,培养应用数学模型解决问题的能力。】
四、进入鸡兔同戏园,演绎抬足法
师:鸡兔同笼问题被我们用假设法破解了,你能用两个字描绘一下你此刻的心情吗?(生:开心、快乐、高兴......)是呀,老师也为你们感到骄傲。假设法有多种思路,除了假设笼子里全是鸡或者全是兔的方法外,“抬足法”也是假设法的一种。现在我们一起进入鸡兔同戏园做“抬足法”游戏吧。
电脑出示游戏规则:我们班61位孩子。把鸡、兔总头数当作61,事先不知自己是鸡还是兔。老师报出总腿数后。听老师指挥,吹第一声口哨,抬左腿;吹第二声口哨,再抬右腿。最后算出鸡、兔各几只?
师报出总腿数为172,开始玩第一次游戏。
师:全体起立(吹第一声口哨,生抬起左腿。)
师:还有多少条腿?(生:172-61=111条)
师吹第二声口哨后笑问:为什么都坐下了?(生:因为没有腿可抬了。)
师:现在还有多少条腿?(生:111-61=50条)
师:剩下的腿是谁的腿?(生:兔子的。)
师:每只兔子还剩下几条腿?(2条)
师:有几只兔子?(50÷2=25只)
师:鸡呢?(生:61-25=36只)
师报出总腿数为162,开始玩第二次游戏。
3. 师:我们又学会了一种解决鸡兔同笼问题的方法,老师给这种方法起个名字——“抬足法”。“抬足法”的形式有多种。试想,兔子和鸡都抬起一半的脚,会怎样呢?这个游戏,孩子们可以课后接着玩。把你所玩的收获写成一篇数学日记交给老师,行吗?
【设计意图:假设法有多种思路,除了假设笼子里全是鸡或者全是兔的方法外,“抬足法”也是假设法的一种。用游戏的方式演绎“抬足法”,使学习资源变得鲜活有趣。“试想,兔子和鸡都抬起一半的脚,会怎样呢?这个游戏,孩子们可以课后接着玩。”以这样的言语激励学生大胆尝试,把鸡兔同笼问题的解决办法进一步拓展。】
畅谈收获,引向纵深。
今天我们解决了一个什么问题?你有什么收获?(选2、3名学生说说)
生1:我学会了用列表法、假设法和抬足法解决鸡兔同笼问题。
师:你的收获真多。
生2:我喜欢用假设法解鸡兔同笼问题,因为假设法解题清楚、明了。
师:很有思想。
生3:我喜欢用抬足法解题,因为抬足法有趣、好玩。
师:有见地。
师:我相信,只要孩子们大胆尝试、积极探究,一定能找到更多、更妙的解决鸡兔同笼问题的方法。
全课教学反思
“鸡兔同笼”问题是我国古代著名的数学趣题,最早出现在《孙子算经》中。解决这类问题有两类方法,一类是“假设法”,古代民间一般是这种方法,另一类是方程解法。“鸡兔同笼”问题在不同版本的教材中都有安排,在人教版2011教材中,这一知识安排在四年级下册数学广角中。教材先说明“鸡兔同笼”问题是我国古代著名的数学问题,再由生动有趣的古代课堂情境引出“鸡兔同笼”原题,并对原题给予解释,由小精灵提出“这个问题你能解决吗”,学生冥思苦想的画面激发学生解决该类问题的兴趣。由于“鸡兔同笼”原题的数据较大,不便于学生进行探究,所以教材以化繁为简的思想为指导,先在例1中安排一道数据较小的“鸡兔同笼”问题让学生探索解决的方法。教材首先呈现了学生最“朴素”的想法——猜测。先猜测鸡、兔各有几只,然后验证脚的只数是否符合条件,如果不对,再猜,这样有时也能找到答案,但有一定的盲目性。下面的表格用来帮助学生按顺序寻找答案,但当数据太大时,不是很合适。这时小精灵提出:还有其他方法吗?让学生去探究更具有逻辑性的解法。教材中主要呈现了“假设法”。回想这堂课,主要有如下体会:
一、尊重学生知识起点,渗透两个思想。
1.渗透化繁为简思想,体会数学的简洁美。
当把《孙子算经》中鸡兔同笼的原题展现在学生面前时,我问:谁会解这道题?学生呈现给我一副苦思瞑想的神态,我及时点拨:为了研究方便,我们可以把数字简化。
当学生用折中列表法和跳跃列表法找到正确答案后,我及时引起学生思考:你所填的鸡、兔、腿数有什么规律?让我们继续完善这张表再观察:鸡、兔、腿的规律。当学生一致统一看法后,我引导学生用两副示意图分别表达假设全是鸡和全是兔的推导过程并配以简洁的文字和算式表述推理。
2.渗透假设法思想,理会解题的内涵。
当学生列表找到鸡、兔、腿的规律后,我适时引导学生把规律转化成一种切实可行的能马上找到答案的方法——假设法。借助图形,学生深刻领悟了假设法的推理过程,减少了差错。用抬足法游戏解题,打开了学生的思路。
恰当运用多媒体,体现多媒体的课堂价值。
古题做成音画,让古朴纯厚的数学气息弥漫于数学课堂。
练习过程中,穿插轻音乐,减少学生练习的疲劳感。
三、多角度提供思考、展示的空间,扎实掌握所学知识。
1.提供思考支点,使学生在思考中完善、验证。在新课教学活动中,当学生理解了题目意思后,我引导学生思考:你可能不能一下子找到答案,但我们可以——先根据什么条件猜?正确与否,还要根据什么条件继续猜?直到——。这样,学生在填表时就会有的放矢。
2.操作中引导思考,使学生内化知识。在教学用假设法解决例题中的鸡兔同笼问题时,我引导学生借助图形边画边思考,并把这种思考和画图的过程转化成文字和算式,内化了鸡兔同笼问题的知识,建立了数学模型。
3.尊重学生思维,为学生提供展示、交流的机会。教学过程中,充分尊重学生的思维,提供给学生充裕的展示、交流的机会,如例题中的表格的完善来自于多名学生的表格填写数据,新课教学中第二副示意图和思维过程的表达是由一名学生充当小老师进行讲解,再由学生质疑、释疑、评价。在推广应用中,我把话语权交给学生,由学生表达解题的全过程,让学生享受到解题的乐趣。
四、多种形式开展合作学习,感受学习数学的乐趣。
1.表格的填写由多名学生猜想、调整、完善。
2.表格的规律采取同桌说一说,4人一小组组织说,代表展示说等形式分享学习成果和快乐。
3.借助游戏演绎“抬足法”。课尾,我组织学生在哨声中演绎“抬足法”,在欢快和谐的气氛中把课推向高潮。
五、发挥生生间、师生间的评价功能。
1.展示汇报中进行评价。学生每上台展示一次小组的成果都让学生来质疑评价“小老师”的表现。
2.学习园地中进行评价。每一次学习园地的学习活动结束时进行评价。
整堂课,依托三块学习原地,本着用多种形式建立“假设法”解决鸡兔同笼的数学模型、多种学习方式内化数学知识、多种渠道拓宽学生的解题思路、多角度引领数学思考的教学原则,使学生在乐中学,趣中学,玩中学。
