华东师大版初中数学九年级下册第27章圆单元综合测试5含答案
文档属性
| 名称 | 华东师大版初中数学九年级下册第27章圆单元综合测试5含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 55.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 13:44:35 | ||
图片预览



文档简介
第27章 圆
单元测试
一、选择题
1.下列条件中,能确定圆的是( )
A.以已知点O为圆心 B.以1cm长为半径
C.经过已知点A,且半径为2cm D.以点O为圆心,1cm为半径
2.如图1所示,AB是⊙O直径,弦CD⊥AB于E,AB=10,CD=8,则AE长为( )
A.2 B.3 C.4 D.5
(1) (2) (3)
3.如图2所示,A是半径为5的⊙O内一点,且OA=3,过点A且长等于7的弦有( )
A.0条 B.1条 C.2条 D.无数条
4.同圆内两条互相平行且相等的弦所对的圆心角为65°, 则此两弦所夹的两条劣弧所对的圆周角之和是( )
A.65° B.130° C.230° D.115°
5.下列说法正确的是( )
A.经过三个点有且只有一个圆;
B.经过两点的圆的圆心是这两点连线的中点
C.钝角三角形的外心在三角形外部;
D.等腰三角形的外心即为其中心
6.已知⊙O半径为4,直线L与⊙O不相交,则圆心到直线L的距离d( )
A.d>4 B.d=4 C.d≥4 D.d≤4
7.如图3所示,AB为⊙O直径,P点在AB延长线上,PM切⊙O于M点,若OA=a,PM=a,则△PMB周长是( )
A.(2+)a B.2- C.(2-)a D.2+
8.如图4所示,在工地的水平面上,有三根直径均为1m的水泥管两两相切叠在一起,则其最高点到地面的距离是( )
A.2 B.(1+)m C.()m D.(1+)m
(4) (5) (6)
9.如图5所示,正方形边长为a,分别以它的4条边为直径作半圆, 则圆中阴影部分面积为( )
A.(-1)a2 B.a2 C.(-1)a2 D.(-1)a2
10.工人师傅在一个长为25cm,宽为18cm的矩形铁皮上, 剪去一个和三边都相切的圆A后,在剩余部分的废料上再剪出一个最大的圆,圆的直径是( )
A.7cm B.8cm C.7cm D.4cm
二、填空题
1.圆的一条弦把直径分成4cm和8cm两部分,并且弦和直径相交成60°,那么该弦的长为_________.
2.如图6所示,AB、AC为⊙O的两条弦,延长CA到点D,AD=DB,若∠ADB=35°,则∠BOC=________.
3.直角三角形的外心是________中点,锐角三角形外心在三角形________,钝角三角形外心在三角形________.
4.如果大圆半径是小圆半径的2倍,当两圆内切时,圆心距为5cm, 那么这两圆外切时,圆心距是_______cm.
5. 直角三角形的两条直角边的长为6cm 和8cm, 则该三角形内切圆的周长为______cm.
6.已知弓形弦长等于R(R为半径),则此弓形的面积为_________.
7.已知圆锥的底面半径为4,母线长为6,则它的侧面积为________.
8.已知圆锥的侧面展开图的面积是15cm2,母线长为5cm,则圆锥的高为_____cm.
9.如图7,PA、PB与⊙O分别相切于点A、B,AC是⊙O直径,PC交⊙O于点D,已知∠APB=60°,AC=2,则CD长为________.
(7) (8) (9)
10.圆锥的轴截面ABC是边长为2的正三角形,如图8所示,动点P从C点出发,沿着圆锥的侧面积移到AB的中点D的最短距离为________.
三、解答题
1.如图9,在Rt△ABC中,∠ACB=90°,AC=4,AB=5,CD⊥AB于D,以C为圆心,2.4为半径作⊙C,试判断A、D、B三点与⊙O位置关系.
2.已知四边形ABCD是⊙O内接梯形,如图所示,⊙O 半径等于5cm, 求梯形ABCD面积.
3.如图所示,⊙O中,弦AB所对的劣弧为圆的,延长AB到C,使OC=AB,OC交⊙O于D,求的度数.
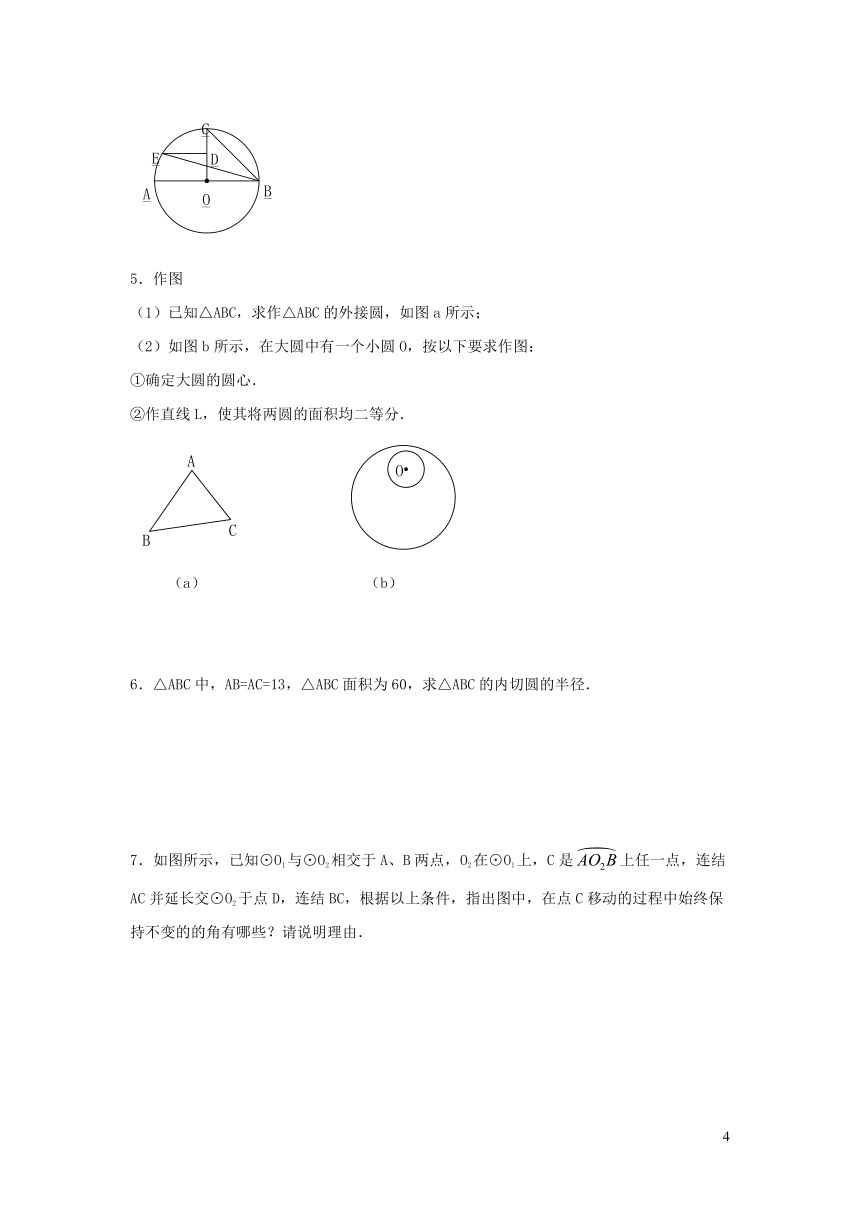
4.如图所示的⊙O中,AB是直径,OC⊥AB,D是OC中点,DE∥AB交⊙O于E, 求∠EBC和∠EBA.
5.作图
(1)已知△ABC,求作△ABC的外接圆,如图a所示;
(2)如图b所示,在大圆中有一个小圆O,按以下要求作图:
①确定大圆的圆心.
②作直线L,使其将两圆的面积均二等分.
(a) (b)
6.△ABC中,AB=AC=13,△ABC面积为60,求△ABC的内切圆的半径.
7.如图所示,已知⊙O1与⊙O2相交于A、B两点,O2在⊙O1上,C是上任一点,连结AC并延长交⊙O2于点D,连结BC,根据以上条件,指出图中,在点C移动的过程中始终保持不变的的角有哪些?请说明理由.
8.如图所示,一个动滑轮的半径为30cm,同一根绳子连接, 绳子与滑轮的接触部分是,绳子AC段与BD段所在的直线成30°角,求接触部分的长.(精确到0.1m)
四、综合应用题
1.如图所示是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形的扇形OAB,经测量,纸杯上开口圆的直径为6cm, 下底面直径为4cm,母线长EF=8cm,求扇形OAB的圆心角及这个纸杯的表面积(面积计算结果用表示)
2.空投物资用的某种降落伞的轴截面如图所示,△ABG是等边三角,C、 D是以AB为直径的半圆O的两个三等分点,CG、DG分别交AB于点E、F,试判断点E、F 分别位于所在线段的什么位置?并证明你的结论(证一种情况即可).
附加题
如图所示,AB是半圆O的直径,点M是直径OA的中点,点P在线段AM上运动( 不与点M重合),点Q在半圆上运动,且总保持PQ=PO.
过Q点作⊙O的切线交BA延长线于点C.
(1)当∠QPA=60°,请你对△QCP的形状做出猜想,并给予证明.
(2)当QP⊥AB时,△QCP形状__________三角形.
(3)由(1)、(2)得出的结论,请进一步猜想点P在线段AM上运动到任何位置时,∠QCP一定是_______三角形.
参考答案
一、1.D 2.A 3.A 4.D 5.C 6.A 7.A 8.D 9.A 10.C
二、1.2cm 2.140° 3.斜边 内 外 4.15 5.4 6.R2
7.12 8.4 9. 10.
三、1.CD==2.4,∵CA>2.4,∴A在⊙C外,
∵CB>2.4,B在⊙C外,∵CD=2.4,∴D在⊙C上.
2.7cm2或49cm2(提示:分AB、CD在圆心O同侧或异侧)
3.提示:过O作OE⊥AB,垂足为E,可证得∠EOC=60°,
∴∠BOD=60°-45°=15°, ∴BD度数为15°.
4.30° 15°(提示:连OE,证∠EOD=60°)
5.略
6.过A作AD⊥BC于D,则BD=DC,
设BD=x,则AD=,
则·2x·=60,x4-169x2+3600=0,x2=25或x2=144,
∴x=5或x=12,∴BC=10或BC=24,∴r==或r=.
7.∠ACB,∠CDB 理由略
8.=·30=20≈62.8m.
四、1.45° 44cm2.
2.点E、F均为所在线段的三等分点,
证明:连结AC、BC,∵C、D是半圆O的三等分点,△ABG是等边三角形,
∴∠CAB=60°=∠ABG,∠ACB=90°,
∴AC=AB=BG,AC∥BG,∴=,
故点E为AB和CG的三等分点.
附加题:(1)当∠QPA=60°时,△QCP为等边三角形,连结OQ,
∵QC为半圆切线, ∴OQ⊥CQ,
∵PQ=PO,∴∠PQO=30°,∴PQC=60°,
又∵∠QPA=60°,∴∠C= 60 °,
∴△QCP为等边三角形.
(2)等腰直角
(3)等腰
单元测试
一、选择题
1.下列条件中,能确定圆的是( )
A.以已知点O为圆心 B.以1cm长为半径
C.经过已知点A,且半径为2cm D.以点O为圆心,1cm为半径
2.如图1所示,AB是⊙O直径,弦CD⊥AB于E,AB=10,CD=8,则AE长为( )
A.2 B.3 C.4 D.5
(1) (2) (3)
3.如图2所示,A是半径为5的⊙O内一点,且OA=3,过点A且长等于7的弦有( )
A.0条 B.1条 C.2条 D.无数条
4.同圆内两条互相平行且相等的弦所对的圆心角为65°, 则此两弦所夹的两条劣弧所对的圆周角之和是( )
A.65° B.130° C.230° D.115°
5.下列说法正确的是( )
A.经过三个点有且只有一个圆;
B.经过两点的圆的圆心是这两点连线的中点
C.钝角三角形的外心在三角形外部;
D.等腰三角形的外心即为其中心
6.已知⊙O半径为4,直线L与⊙O不相交,则圆心到直线L的距离d( )
A.d>4 B.d=4 C.d≥4 D.d≤4
7.如图3所示,AB为⊙O直径,P点在AB延长线上,PM切⊙O于M点,若OA=a,PM=a,则△PMB周长是( )
A.(2+)a B.2- C.(2-)a D.2+
8.如图4所示,在工地的水平面上,有三根直径均为1m的水泥管两两相切叠在一起,则其最高点到地面的距离是( )
A.2 B.(1+)m C.()m D.(1+)m
(4) (5) (6)
9.如图5所示,正方形边长为a,分别以它的4条边为直径作半圆, 则圆中阴影部分面积为( )
A.(-1)a2 B.a2 C.(-1)a2 D.(-1)a2
10.工人师傅在一个长为25cm,宽为18cm的矩形铁皮上, 剪去一个和三边都相切的圆A后,在剩余部分的废料上再剪出一个最大的圆,圆的直径是( )
A.7cm B.8cm C.7cm D.4cm
二、填空题
1.圆的一条弦把直径分成4cm和8cm两部分,并且弦和直径相交成60°,那么该弦的长为_________.
2.如图6所示,AB、AC为⊙O的两条弦,延长CA到点D,AD=DB,若∠ADB=35°,则∠BOC=________.
3.直角三角形的外心是________中点,锐角三角形外心在三角形________,钝角三角形外心在三角形________.
4.如果大圆半径是小圆半径的2倍,当两圆内切时,圆心距为5cm, 那么这两圆外切时,圆心距是_______cm.
5. 直角三角形的两条直角边的长为6cm 和8cm, 则该三角形内切圆的周长为______cm.
6.已知弓形弦长等于R(R为半径),则此弓形的面积为_________.
7.已知圆锥的底面半径为4,母线长为6,则它的侧面积为________.
8.已知圆锥的侧面展开图的面积是15cm2,母线长为5cm,则圆锥的高为_____cm.
9.如图7,PA、PB与⊙O分别相切于点A、B,AC是⊙O直径,PC交⊙O于点D,已知∠APB=60°,AC=2,则CD长为________.
(7) (8) (9)
10.圆锥的轴截面ABC是边长为2的正三角形,如图8所示,动点P从C点出发,沿着圆锥的侧面积移到AB的中点D的最短距离为________.
三、解答题
1.如图9,在Rt△ABC中,∠ACB=90°,AC=4,AB=5,CD⊥AB于D,以C为圆心,2.4为半径作⊙C,试判断A、D、B三点与⊙O位置关系.
2.已知四边形ABCD是⊙O内接梯形,如图所示,⊙O 半径等于5cm, 求梯形ABCD面积.
3.如图所示,⊙O中,弦AB所对的劣弧为圆的,延长AB到C,使OC=AB,OC交⊙O于D,求的度数.
4.如图所示的⊙O中,AB是直径,OC⊥AB,D是OC中点,DE∥AB交⊙O于E, 求∠EBC和∠EBA.
5.作图
(1)已知△ABC,求作△ABC的外接圆,如图a所示;
(2)如图b所示,在大圆中有一个小圆O,按以下要求作图:
①确定大圆的圆心.
②作直线L,使其将两圆的面积均二等分.
(a) (b)
6.△ABC中,AB=AC=13,△ABC面积为60,求△ABC的内切圆的半径.
7.如图所示,已知⊙O1与⊙O2相交于A、B两点,O2在⊙O1上,C是上任一点,连结AC并延长交⊙O2于点D,连结BC,根据以上条件,指出图中,在点C移动的过程中始终保持不变的的角有哪些?请说明理由.
8.如图所示,一个动滑轮的半径为30cm,同一根绳子连接, 绳子与滑轮的接触部分是,绳子AC段与BD段所在的直线成30°角,求接触部分的长.(精确到0.1m)
四、综合应用题
1.如图所示是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥,该圆锥的侧面展开图形的扇形OAB,经测量,纸杯上开口圆的直径为6cm, 下底面直径为4cm,母线长EF=8cm,求扇形OAB的圆心角及这个纸杯的表面积(面积计算结果用表示)
2.空投物资用的某种降落伞的轴截面如图所示,△ABG是等边三角,C、 D是以AB为直径的半圆O的两个三等分点,CG、DG分别交AB于点E、F,试判断点E、F 分别位于所在线段的什么位置?并证明你的结论(证一种情况即可).
附加题
如图所示,AB是半圆O的直径,点M是直径OA的中点,点P在线段AM上运动( 不与点M重合),点Q在半圆上运动,且总保持PQ=PO.
过Q点作⊙O的切线交BA延长线于点C.
(1)当∠QPA=60°,请你对△QCP的形状做出猜想,并给予证明.
(2)当QP⊥AB时,△QCP形状__________三角形.
(3)由(1)、(2)得出的结论,请进一步猜想点P在线段AM上运动到任何位置时,∠QCP一定是_______三角形.
参考答案
一、1.D 2.A 3.A 4.D 5.C 6.A 7.A 8.D 9.A 10.C
二、1.2cm 2.140° 3.斜边 内 外 4.15 5.4 6.R2
7.12 8.4 9. 10.
三、1.CD==2.4,∵CA>2.4,∴A在⊙C外,
∵CB>2.4,B在⊙C外,∵CD=2.4,∴D在⊙C上.
2.7cm2或49cm2(提示:分AB、CD在圆心O同侧或异侧)
3.提示:过O作OE⊥AB,垂足为E,可证得∠EOC=60°,
∴∠BOD=60°-45°=15°, ∴BD度数为15°.
4.30° 15°(提示:连OE,证∠EOD=60°)
5.略
6.过A作AD⊥BC于D,则BD=DC,
设BD=x,则AD=,
则·2x·=60,x4-169x2+3600=0,x2=25或x2=144,
∴x=5或x=12,∴BC=10或BC=24,∴r==或r=.
7.∠ACB,∠CDB 理由略
8.=·30=20≈62.8m.
四、1.45° 44cm2.
2.点E、F均为所在线段的三等分点,
证明:连结AC、BC,∵C、D是半圆O的三等分点,△ABG是等边三角形,
∴∠CAB=60°=∠ABG,∠ACB=90°,
∴AC=AB=BG,AC∥BG,∴=,
故点E为AB和CG的三等分点.
附加题:(1)当∠QPA=60°时,△QCP为等边三角形,连结OQ,
∵QC为半圆切线, ∴OQ⊥CQ,
∵PQ=PO,∴∠PQO=30°,∴PQC=60°,
又∵∠QPA=60°,∴∠C= 60 °,
∴△QCP为等边三角形.
(2)等腰直角
(3)等腰
