2019-2020学年八年级数学上册第十一章三角形11.2与三角形有关的角同步练习(含解析)
文档属性
| 名称 | 2019-2020学年八年级数学上册第十一章三角形11.2与三角形有关的角同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 269.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览




文档简介
第十一章 三角形
第二节 与三角形有关的角
一、单选题(共10小题)
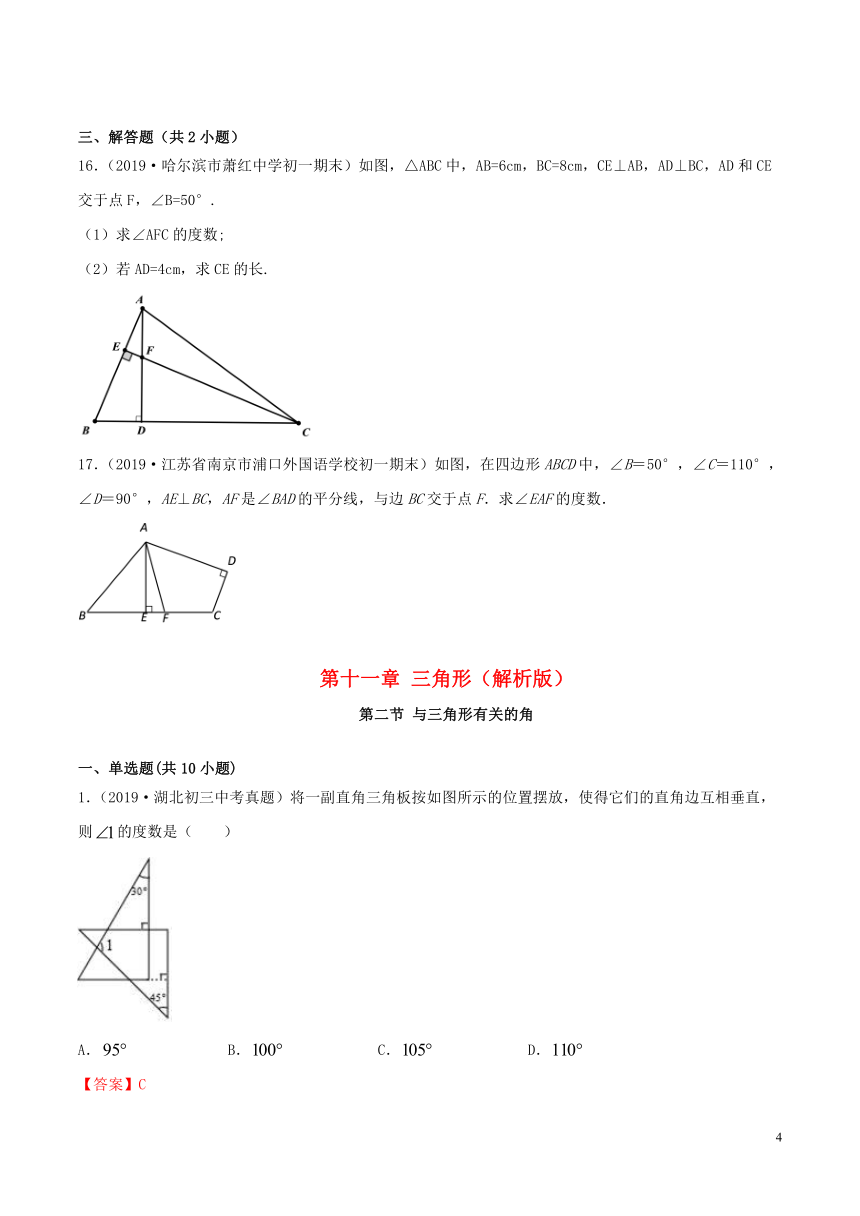
1.(2019·湖北初三中考真题)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则的度数是( )
A. B. C. D.
2.(2019·甘肃初三中考真题)一把直尺和一块三角板(含、角)如图所示摆放,直尺一边与三角板的两直角边分别交于点和点,另一边与三角板的两直角边分别交于点和点,且,那么的大小为( )
A. B. C. D.
3.(2019·河南初三中考真题)如图,,,,则的度数为( )
A. B. C. D.
4.(2019·哈尔滨市萧红中学初一期末)如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,,,,则的度数是( ).
A.117° B.120° C.132° D.107°
5.(2019·浙江初三中考真题)如图,墙上钉着三根木条,量得,,那么木条所在直线所夹的锐角是( )
A. B. C. D.
6.(2019·单县启智学校初一期末)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
7.(2019·四川初三中考真题)如图,直线∥,点在上,且.若,那么等于( )
A. B. C. D.
8.(2019·哈尔滨风华中学初一期中)如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ).
A.110° B.180° C.290° D.310°
9.(2019·江苏省兴化市乐吾实验学校初一期中)下列说法中,正确的个数为( )
①三角形的高、中线、角平分线都是线段
②三角形的外角大于任意一个内角
③△ABC中,∠A=2∠B=3∠C,则△ABC是直角三角形
④若a、b、c均大于0,且满足a+b>c,则长为a、b、c的三条线段一定能组成三角形
A.1 B.2 C.3 D.4
10.(2019·深圳实验学校中学部初一期中)如图,AB∥CD,AD与BC相交于点O,若∠A=50°,∠COD=100°,则∠C等于
A.50° B.100° C.30° D.150°
二、填空题(共5小题)
11.(2019·哈尔滨风华中学初一期中)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=30°,∠BCA=100°,则∠DAE的度数为______.
12.(2019·重庆市永川区红炉镇红炉初级中学校初二期中)等腰三角形的一个角是100°, 则它的底角度数是____________°.
13.(2019·吉林长春外国语学校初一期中)已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是_____________
14.(2019·宜兴市新芳中学初一期中)在△ABC中,∠A=60°,∠B=2∠C,则∠B=_______ °.
15.(2019·江苏省泰兴市黄桥初级中学初一期中)在中,,则 ______ .
三、解答题(共2小题)
16.(2019·哈尔滨市萧红中学初一期末)如图,△ABC中,AB=6cm,BC=8cm,CE⊥AB,AD⊥BC,AD和CE交于点F,∠B=50°.
(1)求∠AFC的度数;
(2)若AD=4cm,求CE的长.
17.(2019·江苏省南京市浦口外国语学校初一期末)如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
第十一章 三角形(解析版)
第二节 与三角形有关的角
一、单选题(共10小题)
1.(2019·湖北初三中考真题)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则的度数是( )
A. B. C. D.
【答案】C
【解析】根据题意求出、,根据对顶角的性质、三角形的外角性质计算即可.
【详解】由题意得,,
,
由三角形的外角性质可知,,
故选C.
【点睛】本题考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
2.(2019·甘肃初三中考真题)一把直尺和一块三角板(含、角)如图所示摆放,直尺一边与三角板的两直角边分别交于点和点,另一边与三角板的两直角边分别交于点和点,且,那么的大小为( )
A. B. C. D.
【答案】B
【解析】先利用三角形外角性质得到∠FDE=∠C+∠CED=140°,然后根据平行线的性质得到∠BFA的度数.
【详解】,
∵,
∴.
故选:B.
【点睛】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
3.(2019·河南初三中考真题)如图,,,,则的度数为( )
A. B. C. D.
【答案】B
【解析】根据平行线的性质解答即可.
【详解】
解:,
,
,
,
故选:B.
【点睛】本题考查平行线的性质,关键是根据平行线的性质解答.
4.(2019·哈尔滨市萧红中学初一期末)如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,,,,则的度数是( ).
A.117° B.120° C.132° D.107°
【答案】A
【解析】根据题意得∠BDC=97?,再证明∠EFC=∠BFD.再根据外角和定理,即可计算出∠BFC的度数.
【详解】在△ACD中,∵∠A=62°,∠ACD=35°
∴∠BDC=∠A+∠ACD=62°+35°=97°;
在△BDF中,∵∠BDC+∠ABE+∠BFD=180°,∠ABE=20°,
∴∠BFD=180°?97°?20°=63°,
∴∠EFC=∠BFD=63°(对顶角相等).
=180°-63°=117°
故选A
【点睛】本题考查外角和定理,熟练掌握性质定理是解题关键.
5.(2019·浙江初三中考真题)如图,墙上钉着三根木条,量得,,那么木条所在直线所夹的锐角是( )
A. B. C. D.
【答案】B
【解析】根据对顶角相等求出∠3,根据三角形内角和定理计算,得到答案.
【详解】如图,
∠3=∠2=100°,
∴木条a,b所在直线所夹的锐角=180°-100°-70°=10°,
故选B.
【点睛】本题考查的是三角形内角和定理、对顶角的性质,掌握三角形内角和等于180°是解题的关键.
6.(2019·单县启智学校初一期末)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
【答案】B
【解析】先根据平行线的性质求出∠BEF的值,再根据三角形的外角等于不相邻两个内角的和求出∠A的度数即可.
【详解】∵AB∥CD,∠C=70°,
∴∠BEF=∠C=70°,
∵∠F=30°,
∴∠A=70°-30°=40°.
故选B.
【点睛】本题考查了平行线的性质:①两直线平行同位角相等,②两直线平行内错角相等,③两直线平行同旁内角互补.在运用平行线的性质定理时,一定要找准同位角,内错角和同旁内角.也考查了三角形外角的性质.
7.(2019·四川初三中考真题)如图,直线∥,点在上,且.若,那么等于( )
A. B. C. D.
【答案】C
【解析】根据两直线平行内错角相等可知∠1=∠BAC=35°,由三角形内角和为180°可得∠BCA=180°-90°-35°=55°,故根据对顶角可得∠2.
【详解】解:∵直线a∥b
∴∠1=∠BAC=35°
又∵∠ABC=90°,
∴∠BCA=180°-90°-35°=55°
∴∠2=∠BCA=55°
故选C.
【点睛】本题考查了平行线的性质,三角形内角和定理,对顶角相等,灵活运用是解题的关键.
8.(2019·哈尔滨风华中学初一期中)如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ).
A.110° B.180° C.290° D.310°
【答案】C
【解析】由已知易得∠B+∠C=70°,结合四边形内角和为360°,即可解得∠1+∠2的值了.
【详解】∵在△ABC中,∠A=110°,
∴∠B+∠C=70°,
∵在四边形ABMN中,∠B+∠C +∠1+∠2=360°,
∴∠BMN+∠ANM=360°-70°=290°.
故答案为C.
【点睛】本题考查三角形和四边形内角和的性质,熟知:“三角形内角和为180°,四边形内角和为360°”是解答本题的关键.
9.(2019·江苏省兴化市乐吾实验学校初一期中)下列说法中,正确的个数为( )
①三角形的高、中线、角平分线都是线段
②三角形的外角大于任意一个内角
③△ABC中,∠A=2∠B=3∠C,则△ABC是直角三角形
④若a、b、c均大于0,且满足a+b>c,则长为a、b、c的三条线段一定能组成三角形
A.1 B.2 C.3 D.4
【答案】A
【解析】①三角形的高、中线、角平分线判断即可;②根据三角形的外角的性质即可判断;③利用三角形的内角和是180°求得各角的度数即可判断,④根据三角形三边关系解答.
【详解】解:①三角形的高、中线、角平分线都是线段,正确;
②三角形的外角大于任意一个与它不相邻的内角,错误;
③△ABC中,∠A=2∠B=3∠C,则△ABC不是直角三角形,错误;
④满足a+b>c且a<c,b<c的a、b、c三条线段一定能组成三角形,故错误;
故选:A.
【点睛】本题主要考查的是三角形的外角的性质与内角和定理、三角形的高线,掌握三角形的外角的性质与内角和定理以及三角形的高线特点是解题的关键.
10.(2019·深圳实验学校中学部初一期中)如图,AB∥CD,AD与BC相交于点O,若∠A=50°,∠COD=100°,则∠C等于
A.50° B.100° C.30° D.150°
【答案】C
【解析】根据平行线性质求出∠D,根据三角形的内角和定理得出∠C=180°-∠D-∠COD,代入求出即可.
【详解】解:∵AB∥CD,
∴∠D=∠A=50°,
∵∠COD=100°,
∴∠C=180°-∠D-∠COD=30°,
故选:C.
【点睛】本题考查了三角形的内角和定理和平行线的性质的应用,关键是求出∠D的度数和得出∠C=180°-∠D-∠COD.
(
提升篇
)
二、填空题(共5小题)
11.(2019·哈尔滨风华中学初一期中)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=30°,∠BCA=100°,则∠DAE的度数为______.
【答案】35°
【解析】根据垂直的定义即可得到∠D=90°,根据邻补角的定义可得∠ACD=180°-100°=80°,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE==25°,即可得到结论.
【详解】∵AD⊥BC
∴∠D=90°
∵∠ACB=100°
∴ACD=180-100°=80
∴∠CAD=90°-80°=10°
∵∠B=30°
∴∠BAD=90°-30°=60°
∴∠BAC=50°
∵AE平分∠BAC
∴∠CAE==25°
∴∠EAD=∠CAE+∠CAD=35°
【点睛】本题考查三角形的内角和、角平分线的定义,正确识别图形是解题的关键.
12.(2019·重庆市永川区红炉镇红炉初级中学校初二期中)等腰三角形的一个角是100°, 则它的底角度数是____________°.
【答案】40°;
【解析】等腰三角形的一个角为100°,但已知没有明确此角是顶角还是底角,所以应分两种情况进行讨论.
【详解】解:当100°为顶角时,其他两角为40°、40°,
当100°为底角时,等腰三角形的两底角相等,由三角形的内角和定理可知底角不能为100°,
所以它的底角的度数为40°.
故答案为:40.
【点睛】本题考查了等腰三角形的性质及三角形内角和定理;在解决与等腰三角形有关的问题时,由于等腰三角形所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.
13.(2019·吉林长春外国语学校初一期中)已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是_____________
【答案】相等
【解析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠B+∠BAD,再根据∠BAC=∠BAD+∠DAC即可得解.
【详解】由三角形的外角性质,∠ADC=∠B+∠BAD,
∵∠BAC=∠BAD+∠DAC,∠B=∠DAC,
∴∠BAC=∠ADC
故答案为:相等.
【点睛】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.
14.(2019·宜兴市新芳中学初一期中)在△ABC中,∠A=60°,∠B=2∠C,则∠B=_______ °.
【答案】80
【解析】根据三角形的内角和定理和已知条件求得.
【详解】解:∵∠A+∠B+∠C=180°,
又∵∠A=60°,∠B=2∠C,
∵60°+2∠C+∠C=180°,
∴∠C=40°
∴∠B=80°.
故答案为:80.
【点睛】主要考查了三角形的内角和是180°.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
15.(2019·江苏省泰兴市黄桥初级中学初一期中)在中,,则 ______ .
【答案】54°
【解析】设∠C=x,则∠B=3x,∠A=6x,根据三角形内角和为180°,列出x的方程,求出x的值即可.
【详解】设∠C=x,则∠B=3x,∠A=6x,
根据三角形内角和为180°,
可得x+3x+6x=180°,
解得x=18°,
即∠B=3x=54°,
故答案为:54°.
【点睛】考查三角形的内角和定理,掌握三角形的内角和等于是解题的关键.
三、解答题(共2小题)
16.(2019·哈尔滨市萧红中学初一期末)如图,△ABC中,AB=6cm,BC=8cm,CE⊥AB,AD⊥BC,AD和CE交于点F,∠B=50°.
(1)求∠AFC的度数;
(2)若AD=4cm,求CE的长.
【答案】(1)130°
(2)
【解析】(1)根据三角形的内角和和直角三角形的性质解答即可;
(2)利用三角形的面积公式解答即可;
【详解】(1)∵∠B=50°,
∴∠EAF=90°?50°=40°,
∴∠AFE=90°?40°=50°,
∴∠AFC=180°?50°=130°;
(2)∵△ABC中,AB=6cm,BC=8cm,CE⊥AB,AD⊥BC,
∵AD=4cm,
∴AB×CE=BC×AD,
即CE====
【点睛】本题考查三角形的内角和和直角三角形的性质,解题关键在于熟练掌握三角形的性质.
17.(2019·江苏省南京市浦口外国语学校初一期末)如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
【答案】15°.
【解析】先由四边形内角和求出∠BAD的度数,再根据AF是∠BAD的平分线求出∠BAF的值,最后根据直角三角形两锐角互余求出∠BAE即可得到结论.
【详解】在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,
∴∠BAD=360°-∠B-∠C-∠D=360°-50°-110°-90°=110°,
∵AF是∠BAD的平分线,
∴∠BAF=∠BAD=×110°=55°,
∵AE⊥BC,∠B=50°,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠EAF=∠BAF-∠BAE=55°-40°=15°.
【点睛】此题主要考查了四边形内角和定理,角平分线的性质以及直角三角形两锐角互余等知识,熟练掌握这些性质定理是解决此题的关键.
11
第二节 与三角形有关的角
一、单选题(共10小题)
1.(2019·湖北初三中考真题)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则的度数是( )
A. B. C. D.
2.(2019·甘肃初三中考真题)一把直尺和一块三角板(含、角)如图所示摆放,直尺一边与三角板的两直角边分别交于点和点,另一边与三角板的两直角边分别交于点和点,且,那么的大小为( )
A. B. C. D.
3.(2019·河南初三中考真题)如图,,,,则的度数为( )
A. B. C. D.
4.(2019·哈尔滨市萧红中学初一期末)如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,,,,则的度数是( ).
A.117° B.120° C.132° D.107°
5.(2019·浙江初三中考真题)如图,墙上钉着三根木条,量得,,那么木条所在直线所夹的锐角是( )
A. B. C. D.
6.(2019·单县启智学校初一期末)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
7.(2019·四川初三中考真题)如图,直线∥,点在上,且.若,那么等于( )
A. B. C. D.
8.(2019·哈尔滨风华中学初一期中)如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ).
A.110° B.180° C.290° D.310°
9.(2019·江苏省兴化市乐吾实验学校初一期中)下列说法中,正确的个数为( )
①三角形的高、中线、角平分线都是线段
②三角形的外角大于任意一个内角
③△ABC中,∠A=2∠B=3∠C,则△ABC是直角三角形
④若a、b、c均大于0,且满足a+b>c,则长为a、b、c的三条线段一定能组成三角形
A.1 B.2 C.3 D.4
10.(2019·深圳实验学校中学部初一期中)如图,AB∥CD,AD与BC相交于点O,若∠A=50°,∠COD=100°,则∠C等于
A.50° B.100° C.30° D.150°
二、填空题(共5小题)
11.(2019·哈尔滨风华中学初一期中)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=30°,∠BCA=100°,则∠DAE的度数为______.
12.(2019·重庆市永川区红炉镇红炉初级中学校初二期中)等腰三角形的一个角是100°, 则它的底角度数是____________°.
13.(2019·吉林长春外国语学校初一期中)已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是_____________
14.(2019·宜兴市新芳中学初一期中)在△ABC中,∠A=60°,∠B=2∠C,则∠B=_______ °.
15.(2019·江苏省泰兴市黄桥初级中学初一期中)在中,,则 ______ .
三、解答题(共2小题)
16.(2019·哈尔滨市萧红中学初一期末)如图,△ABC中,AB=6cm,BC=8cm,CE⊥AB,AD⊥BC,AD和CE交于点F,∠B=50°.
(1)求∠AFC的度数;
(2)若AD=4cm,求CE的长.
17.(2019·江苏省南京市浦口外国语学校初一期末)如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
第十一章 三角形(解析版)
第二节 与三角形有关的角
一、单选题(共10小题)
1.(2019·湖北初三中考真题)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则的度数是( )
A. B. C. D.
【答案】C
【解析】根据题意求出、,根据对顶角的性质、三角形的外角性质计算即可.
【详解】由题意得,,
,
由三角形的外角性质可知,,
故选C.
【点睛】本题考查的是三角形的外角性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.
2.(2019·甘肃初三中考真题)一把直尺和一块三角板(含、角)如图所示摆放,直尺一边与三角板的两直角边分别交于点和点,另一边与三角板的两直角边分别交于点和点,且,那么的大小为( )
A. B. C. D.
【答案】B
【解析】先利用三角形外角性质得到∠FDE=∠C+∠CED=140°,然后根据平行线的性质得到∠BFA的度数.
【详解】,
∵,
∴.
故选:B.
【点睛】本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
3.(2019·河南初三中考真题)如图,,,,则的度数为( )
A. B. C. D.
【答案】B
【解析】根据平行线的性质解答即可.
【详解】
解:,
,
,
,
故选:B.
【点睛】本题考查平行线的性质,关键是根据平行线的性质解答.
4.(2019·哈尔滨市萧红中学初一期末)如图,D是AB上一点,E是AC上一点,BE,CD相交于点F,,,,则的度数是( ).
A.117° B.120° C.132° D.107°
【答案】A
【解析】根据题意得∠BDC=97?,再证明∠EFC=∠BFD.再根据外角和定理,即可计算出∠BFC的度数.
【详解】在△ACD中,∵∠A=62°,∠ACD=35°
∴∠BDC=∠A+∠ACD=62°+35°=97°;
在△BDF中,∵∠BDC+∠ABE+∠BFD=180°,∠ABE=20°,
∴∠BFD=180°?97°?20°=63°,
∴∠EFC=∠BFD=63°(对顶角相等).
=180°-63°=117°
故选A
【点睛】本题考查外角和定理,熟练掌握性质定理是解题关键.
5.(2019·浙江初三中考真题)如图,墙上钉着三根木条,量得,,那么木条所在直线所夹的锐角是( )
A. B. C. D.
【答案】B
【解析】根据对顶角相等求出∠3,根据三角形内角和定理计算,得到答案.
【详解】如图,
∠3=∠2=100°,
∴木条a,b所在直线所夹的锐角=180°-100°-70°=10°,
故选B.
【点睛】本题考查的是三角形内角和定理、对顶角的性质,掌握三角形内角和等于180°是解题的关键.
6.(2019·单县启智学校初一期末)如图,已知AB∥CD,∠C=70°,∠F=30°,则∠A的度数为( )
A.30° B.40° C.50° D.60°
【答案】B
【解析】先根据平行线的性质求出∠BEF的值,再根据三角形的外角等于不相邻两个内角的和求出∠A的度数即可.
【详解】∵AB∥CD,∠C=70°,
∴∠BEF=∠C=70°,
∵∠F=30°,
∴∠A=70°-30°=40°.
故选B.
【点睛】本题考查了平行线的性质:①两直线平行同位角相等,②两直线平行内错角相等,③两直线平行同旁内角互补.在运用平行线的性质定理时,一定要找准同位角,内错角和同旁内角.也考查了三角形外角的性质.
7.(2019·四川初三中考真题)如图,直线∥,点在上,且.若,那么等于( )
A. B. C. D.
【答案】C
【解析】根据两直线平行内错角相等可知∠1=∠BAC=35°,由三角形内角和为180°可得∠BCA=180°-90°-35°=55°,故根据对顶角可得∠2.
【详解】解:∵直线a∥b
∴∠1=∠BAC=35°
又∵∠ABC=90°,
∴∠BCA=180°-90°-35°=55°
∴∠2=∠BCA=55°
故选C.
【点睛】本题考查了平行线的性质,三角形内角和定理,对顶角相等,灵活运用是解题的关键.
8.(2019·哈尔滨风华中学初一期中)如图,△ABC中∠A=110°,若图中沿虚线剪去∠A,则∠1+∠2 等于( ).
A.110° B.180° C.290° D.310°
【答案】C
【解析】由已知易得∠B+∠C=70°,结合四边形内角和为360°,即可解得∠1+∠2的值了.
【详解】∵在△ABC中,∠A=110°,
∴∠B+∠C=70°,
∵在四边形ABMN中,∠B+∠C +∠1+∠2=360°,
∴∠BMN+∠ANM=360°-70°=290°.
故答案为C.
【点睛】本题考查三角形和四边形内角和的性质,熟知:“三角形内角和为180°,四边形内角和为360°”是解答本题的关键.
9.(2019·江苏省兴化市乐吾实验学校初一期中)下列说法中,正确的个数为( )
①三角形的高、中线、角平分线都是线段
②三角形的外角大于任意一个内角
③△ABC中,∠A=2∠B=3∠C,则△ABC是直角三角形
④若a、b、c均大于0,且满足a+b>c,则长为a、b、c的三条线段一定能组成三角形
A.1 B.2 C.3 D.4
【答案】A
【解析】①三角形的高、中线、角平分线判断即可;②根据三角形的外角的性质即可判断;③利用三角形的内角和是180°求得各角的度数即可判断,④根据三角形三边关系解答.
【详解】解:①三角形的高、中线、角平分线都是线段,正确;
②三角形的外角大于任意一个与它不相邻的内角,错误;
③△ABC中,∠A=2∠B=3∠C,则△ABC不是直角三角形,错误;
④满足a+b>c且a<c,b<c的a、b、c三条线段一定能组成三角形,故错误;
故选:A.
【点睛】本题主要考查的是三角形的外角的性质与内角和定理、三角形的高线,掌握三角形的外角的性质与内角和定理以及三角形的高线特点是解题的关键.
10.(2019·深圳实验学校中学部初一期中)如图,AB∥CD,AD与BC相交于点O,若∠A=50°,∠COD=100°,则∠C等于
A.50° B.100° C.30° D.150°
【答案】C
【解析】根据平行线性质求出∠D,根据三角形的内角和定理得出∠C=180°-∠D-∠COD,代入求出即可.
【详解】解:∵AB∥CD,
∴∠D=∠A=50°,
∵∠COD=100°,
∴∠C=180°-∠D-∠COD=30°,
故选:C.
【点睛】本题考查了三角形的内角和定理和平行线的性质的应用,关键是求出∠D的度数和得出∠C=180°-∠D-∠COD.
(
提升篇
)
二、填空题(共5小题)
11.(2019·哈尔滨风华中学初一期中)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=30°,∠BCA=100°,则∠DAE的度数为______.
【答案】35°
【解析】根据垂直的定义即可得到∠D=90°,根据邻补角的定义可得∠ACD=180°-100°=80°,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE==25°,即可得到结论.
【详解】∵AD⊥BC
∴∠D=90°
∵∠ACB=100°
∴ACD=180-100°=80
∴∠CAD=90°-80°=10°
∵∠B=30°
∴∠BAD=90°-30°=60°
∴∠BAC=50°
∵AE平分∠BAC
∴∠CAE==25°
∴∠EAD=∠CAE+∠CAD=35°
【点睛】本题考查三角形的内角和、角平分线的定义,正确识别图形是解题的关键.
12.(2019·重庆市永川区红炉镇红炉初级中学校初二期中)等腰三角形的一个角是100°, 则它的底角度数是____________°.
【答案】40°;
【解析】等腰三角形的一个角为100°,但已知没有明确此角是顶角还是底角,所以应分两种情况进行讨论.
【详解】解:当100°为顶角时,其他两角为40°、40°,
当100°为底角时,等腰三角形的两底角相等,由三角形的内角和定理可知底角不能为100°,
所以它的底角的度数为40°.
故答案为:40.
【点睛】本题考查了等腰三角形的性质及三角形内角和定理;在解决与等腰三角形有关的问题时,由于等腰三角形所具有的特殊性质,很多题目在已知不明确的情况下,要进行分类讨论,才能正确解题,因此,解决和等腰三角形有关的边角问题时,要仔细认真,避免出错.
13.(2019·吉林长春外国语学校初一期中)已知,如图,△ABC中,∠B=∠DAC,则∠BAC和∠ADC的大小关系是_____________
【答案】相等
【解析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ADC=∠B+∠BAD,再根据∠BAC=∠BAD+∠DAC即可得解.
【详解】由三角形的外角性质,∠ADC=∠B+∠BAD,
∵∠BAC=∠BAD+∠DAC,∠B=∠DAC,
∴∠BAC=∠ADC
故答案为:相等.
【点睛】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图是解题的关键.
14.(2019·宜兴市新芳中学初一期中)在△ABC中,∠A=60°,∠B=2∠C,则∠B=_______ °.
【答案】80
【解析】根据三角形的内角和定理和已知条件求得.
【详解】解:∵∠A+∠B+∠C=180°,
又∵∠A=60°,∠B=2∠C,
∵60°+2∠C+∠C=180°,
∴∠C=40°
∴∠B=80°.
故答案为:80.
【点睛】主要考查了三角形的内角和是180°.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
15.(2019·江苏省泰兴市黄桥初级中学初一期中)在中,,则 ______ .
【答案】54°
【解析】设∠C=x,则∠B=3x,∠A=6x,根据三角形内角和为180°,列出x的方程,求出x的值即可.
【详解】设∠C=x,则∠B=3x,∠A=6x,
根据三角形内角和为180°,
可得x+3x+6x=180°,
解得x=18°,
即∠B=3x=54°,
故答案为:54°.
【点睛】考查三角形的内角和定理,掌握三角形的内角和等于是解题的关键.
三、解答题(共2小题)
16.(2019·哈尔滨市萧红中学初一期末)如图,△ABC中,AB=6cm,BC=8cm,CE⊥AB,AD⊥BC,AD和CE交于点F,∠B=50°.
(1)求∠AFC的度数;
(2)若AD=4cm,求CE的长.
【答案】(1)130°
(2)
【解析】(1)根据三角形的内角和和直角三角形的性质解答即可;
(2)利用三角形的面积公式解答即可;
【详解】(1)∵∠B=50°,
∴∠EAF=90°?50°=40°,
∴∠AFE=90°?40°=50°,
∴∠AFC=180°?50°=130°;
(2)∵△ABC中,AB=6cm,BC=8cm,CE⊥AB,AD⊥BC,
∵AD=4cm,
∴AB×CE=BC×AD,
即CE====
【点睛】本题考查三角形的内角和和直角三角形的性质,解题关键在于熟练掌握三角形的性质.
17.(2019·江苏省南京市浦口外国语学校初一期末)如图,在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,AE⊥BC,AF是∠BAD的平分线,与边BC交于点F.求∠EAF的度数.
【答案】15°.
【解析】先由四边形内角和求出∠BAD的度数,再根据AF是∠BAD的平分线求出∠BAF的值,最后根据直角三角形两锐角互余求出∠BAE即可得到结论.
【详解】在四边形ABCD中,∠B=50°,∠C=110°,∠D=90°,
∴∠BAD=360°-∠B-∠C-∠D=360°-50°-110°-90°=110°,
∵AF是∠BAD的平分线,
∴∠BAF=∠BAD=×110°=55°,
∵AE⊥BC,∠B=50°,
∴∠BAE=90°-∠B=90°-50°=40°,
∴∠EAF=∠BAF-∠BAE=55°-40°=15°.
【点睛】此题主要考查了四边形内角和定理,角平分线的性质以及直角三角形两锐角互余等知识,熟练掌握这些性质定理是解决此题的关键.
11
