人教A版数学必修二1.3空间几何体的表面积与体积(1)同步练习(含答案解析)
文档属性
| 名称 | 人教A版数学必修二1.3空间几何体的表面积与体积(1)同步练习(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 1001.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
1.3空间几何体的表面积与体积(1)
一、选择题
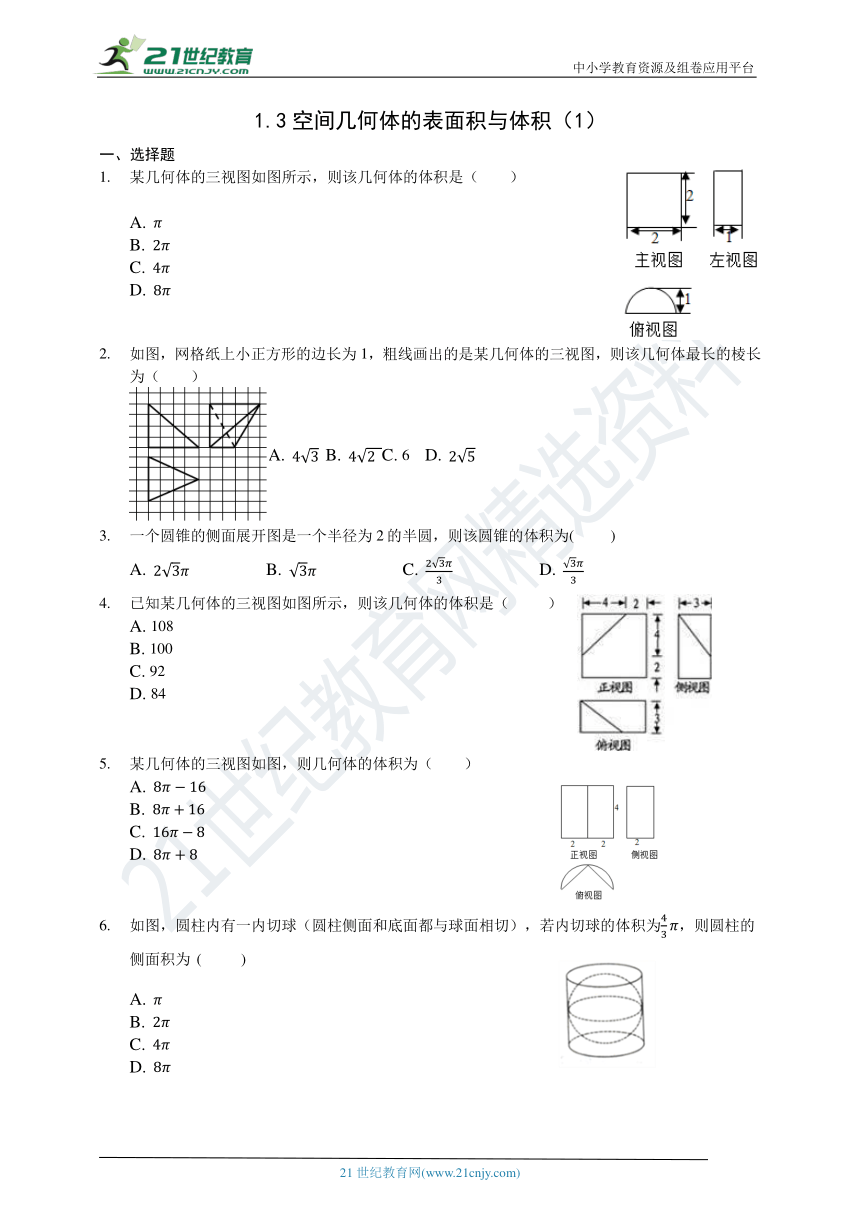
某几何体的三视图如图所示,则该几何体的体积是( )
A.
B.
C.
D.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )
A. B. C. 6 D.
一个圆锥的侧面展开图是一个半径为2的半圆,则该圆锥的体积为( )
A. B. C. D.
已知某几何体的三视图如图所示,则该几何体的体积是( )
A. 108
B. 100
C. 92
D. 84
某几何体的三视图如图,则几何体的体积为( )
A.
B.
C.
D.
如图,圆柱内有一内切球(圆柱侧面和底面都与球面相切),若内切球的体积为,则圆柱的侧面积为 (? ? ? ? )
A.
B.
C.
D.
已知某几何体的三视图如图,则该几何体的表面积是( )
A.
B.
C.
D.
一个几何体三视图如图所示,则该几何体的表面积等于( )
A.
B.
C.
D.
二、填空题
已知正四棱锥的底面边长是,侧棱长是,则该正四棱锥的体积为? ? ? ?.
若圆锥底面半径为2,高为,则其侧面积为______ .
三、解答题
已知四棱锥P-ABCD的体积为,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
答案和解析
1.A解:由三视图可知,该几何体为底面直径为2,高为2的圆柱的一半.
体积V==π.故选A.
2.C解:如图所示,其中,正方体棱长为4,点P是正方体其中一条棱的中点,
则:,,所以最长棱为6.
3.D解:圆锥的侧面展开恰为一个半径为2的半圆,所以圆锥的底面周长为:2π,底面半径为:1,圆锥的高为:;圆锥的体积为:=π.
4.B解:由已知中的三视图可得:该几何体是一个长方体切去一个三棱锥得到的组合体,长方体的体积为:6×6×3=108,棱锥的体积为:××4×3×4=8,
故组合体的体积V=108-8=100,故选B.
5.A解:由已知中的三视图可得:该几何体是一个半圆柱切去一个三棱柱所得的几何体,半圆柱的底面半径为2,高为4,故体积V=π?22?4=8π,
三棱柱的体积V=×4×2×4=16,故几何体的体积V=8π-16.
6.C解:由,可得球的半径r=1,可得圆柱的高为2r=2,圆柱的底面周长为2πr=2π,则圆柱的侧面积为2π2=4π,
7.C?解:根据三视图知,该几何体是底面为等腰三角形,高为2的直三棱柱,画出几何体的直观图,如图所示,结合图中数据,计算它的表面积是
S三棱柱=2××2×1+2×2+2×2+2×2=6+8.
?8.C解:由三视图可知:该几何体为圆锥沿轴截取的一半.
∴该几何体的表面积=++=6+π.
9.解:如图,正四棱锥P-ABCD中,AB=2,PA=,
设正四棱锥的高为PO,连结AO,
则AO=AC=.在直角三角形POA中,
?PO===1.
所以=??PO=×4×1=.
10.6π解:∵圆锥的底面半径为2,高为,∴母线长为:=3,
∴圆锥的侧面积为:πrl=π×2×3=6π,故答案为:6π.
11.解:(1)如图所示四棱锥P-ABCD的高为PA,底面积为S=?CD=×1=
∴四棱锥P-ABCD的体积V四棱锥P-ABCD=S?PA=×?PA=.解得PA=
∴正视图的面积为S=×2×=.
(2)如图所示,过A作AE∥CD交BC于E,连结PE.
根据三视图可知,E是BC的中点,
且BE=CE=1,AE=CD=1,且BC⊥AE,AB=
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD=
∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,
∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE=.
∴四棱锥P-ABCD的侧面积为
S=S△PAB+S△PAD+S△PCD+S△PBC=??+??1+?1?+?2?=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
1.3空间几何体的表面积与体积(1)
一、选择题
某几何体的三视图如图所示,则该几何体的体积是( )
A.
B.
C.
D.
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )
A. B. C. 6 D.
一个圆锥的侧面展开图是一个半径为2的半圆,则该圆锥的体积为( )
A. B. C. D.
已知某几何体的三视图如图所示,则该几何体的体积是( )
A. 108
B. 100
C. 92
D. 84
某几何体的三视图如图,则几何体的体积为( )
A.
B.
C.
D.
如图,圆柱内有一内切球(圆柱侧面和底面都与球面相切),若内切球的体积为,则圆柱的侧面积为 (? ? ? ? )
A.
B.
C.
D.
已知某几何体的三视图如图,则该几何体的表面积是( )
A.
B.
C.
D.
一个几何体三视图如图所示,则该几何体的表面积等于( )
A.
B.
C.
D.
二、填空题
已知正四棱锥的底面边长是,侧棱长是,则该正四棱锥的体积为? ? ? ?.
若圆锥底面半径为2,高为,则其侧面积为______ .
三、解答题
已知四棱锥P-ABCD的体积为,其三视图如图所示,其中正视图为等腰三角形,侧视图为直角三角形,俯视图是直角梯形.
(1)求正视图的面积;
(2)求四棱锥P-ABCD的侧面积.
答案和解析
1.A解:由三视图可知,该几何体为底面直径为2,高为2的圆柱的一半.
体积V==π.故选A.
2.C解:如图所示,其中,正方体棱长为4,点P是正方体其中一条棱的中点,
则:,,所以最长棱为6.
3.D解:圆锥的侧面展开恰为一个半径为2的半圆,所以圆锥的底面周长为:2π,底面半径为:1,圆锥的高为:;圆锥的体积为:=π.
4.B解:由已知中的三视图可得:该几何体是一个长方体切去一个三棱锥得到的组合体,长方体的体积为:6×6×3=108,棱锥的体积为:××4×3×4=8,
故组合体的体积V=108-8=100,故选B.
5.A解:由已知中的三视图可得:该几何体是一个半圆柱切去一个三棱柱所得的几何体,半圆柱的底面半径为2,高为4,故体积V=π?22?4=8π,
三棱柱的体积V=×4×2×4=16,故几何体的体积V=8π-16.
6.C解:由,可得球的半径r=1,可得圆柱的高为2r=2,圆柱的底面周长为2πr=2π,则圆柱的侧面积为2π2=4π,
7.C?解:根据三视图知,该几何体是底面为等腰三角形,高为2的直三棱柱,画出几何体的直观图,如图所示,结合图中数据,计算它的表面积是
S三棱柱=2××2×1+2×2+2×2+2×2=6+8.
?8.C解:由三视图可知:该几何体为圆锥沿轴截取的一半.
∴该几何体的表面积=++=6+π.
9.解:如图,正四棱锥P-ABCD中,AB=2,PA=,
设正四棱锥的高为PO,连结AO,
则AO=AC=.在直角三角形POA中,
?PO===1.
所以=??PO=×4×1=.
10.6π解:∵圆锥的底面半径为2,高为,∴母线长为:=3,
∴圆锥的侧面积为:πrl=π×2×3=6π,故答案为:6π.
11.解:(1)如图所示四棱锥P-ABCD的高为PA,底面积为S=?CD=×1=
∴四棱锥P-ABCD的体积V四棱锥P-ABCD=S?PA=×?PA=.解得PA=
∴正视图的面积为S=×2×=.
(2)如图所示,过A作AE∥CD交BC于E,连结PE.
根据三视图可知,E是BC的中点,
且BE=CE=1,AE=CD=1,且BC⊥AE,AB=
又PA⊥平面ABCD,∴PA⊥BC,PA⊥DC,PD=
∴BC⊥面PAE,∴BC⊥PE,
又DC⊥AD,∴DC⊥面PAD,
∴DC⊥PD,且PA⊥平面ABCD.∴PA⊥AE,
∴PE2=PA2+AE2=3.∴PE=.
∴四棱锥P-ABCD的侧面积为
S=S△PAB+S△PAD+S△PCD+S△PBC=??+??1+?1?+?2?=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
