北师大版七年级下册:2.2 探索直线平行的条件 同步练习(含答案)
文档属性
| 名称 | 北师大版七年级下册:2.2 探索直线平行的条件 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 161.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览


文档简介
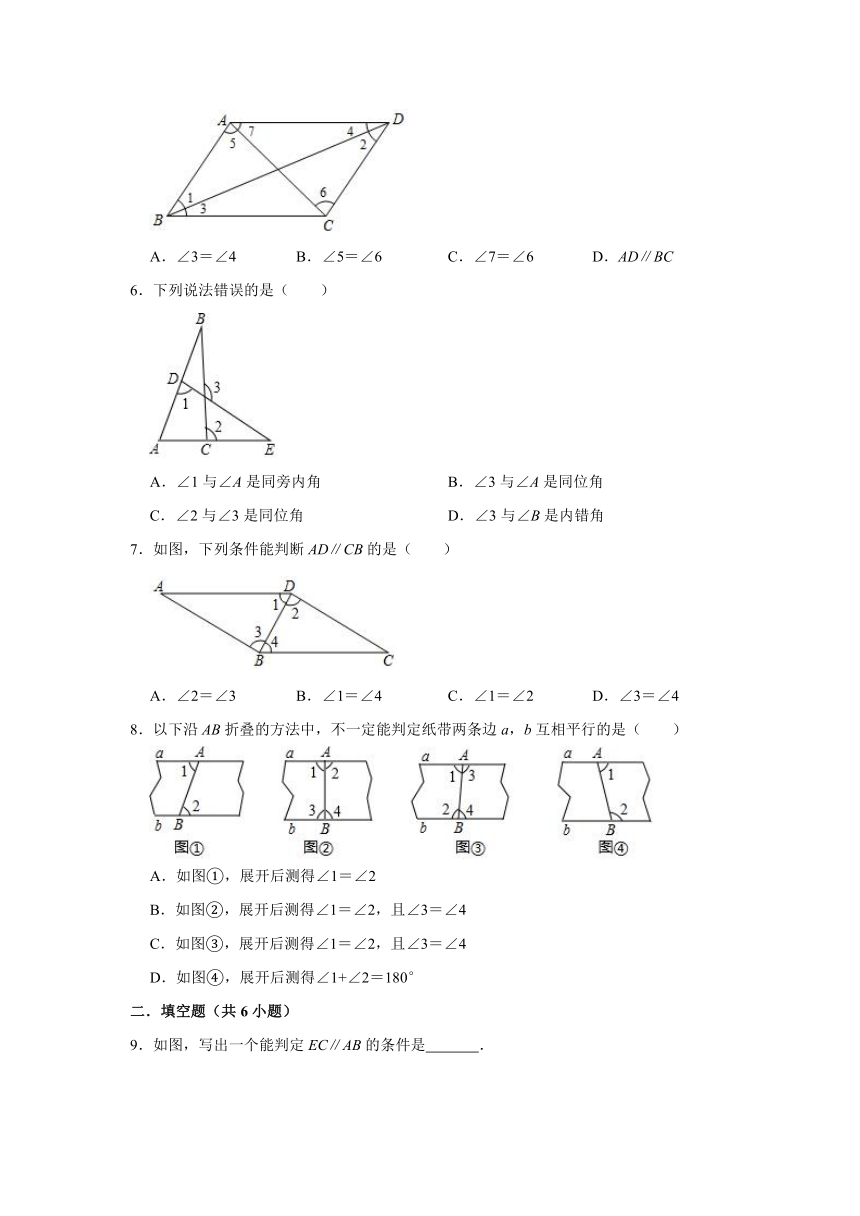
北师大版七年级下册:2.2 探索直线平行的条件 同步练习
一.选择题(共8小题)
1.如图,图中的内错角有( )对.
A.5 B.7 C.8 D.10
2.如图,∠1和∠2是直线( )和直线( )被直线( )所截得到的.应选( )
A.a,b,c,同旁内角 B.a,c,b,同位角
C.a,b,c,同位角 D.c,b,a,同位角
3.如图所示,下列条件中,不能判断AD∥BC的是( )
A.∠1=∠4 B.∠3=∠4 C.∠2+∠3=180° D.∠1+∠D=180°
4.如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6+∠4=180°;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
5.如图,由∠1=∠2得到的结论正确的是( )
A.∠3=∠4 B.∠5=∠6 C.∠7=∠6 D.AD∥BC
6.下列说法错误的是( )
A.∠1与∠A是同旁内角 B.∠3与∠A是同位角
C.∠2与∠3是同位角 D.∠3与∠B是内错角
7.如图,下列条件能判断AD∥CB的是( )
A.∠2=∠3 B.∠1=∠4 C.∠1=∠2 D.∠3=∠4
8.以下沿AB折叠的方法中,不一定能判定纸带两条边a,b互相平行的是( )
A.如图①,展开后测得∠1=∠2
B.如图②,展开后测得∠1=∠2,且∠3=∠4
C.如图③,展开后测得∠1=∠2,且∠3=∠4
D.如图④,展开后测得∠1+∠2=180°
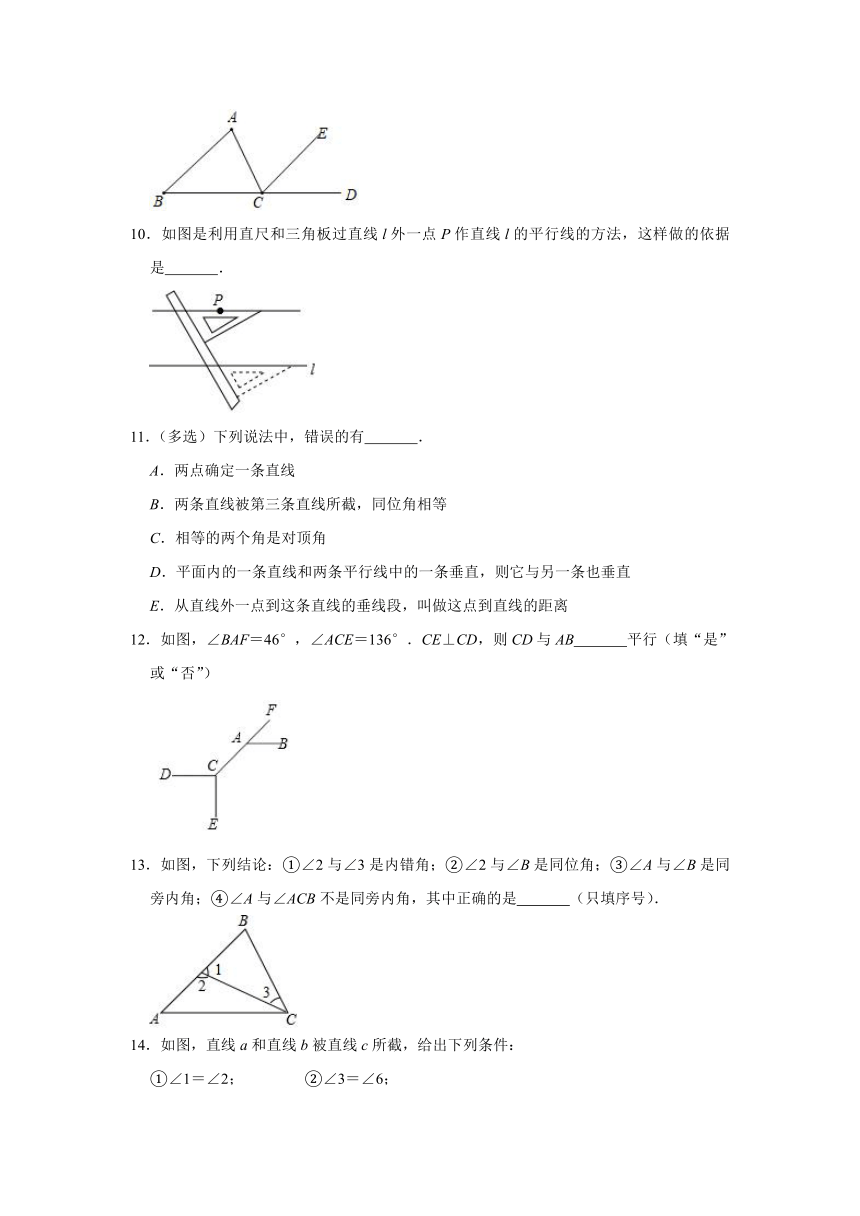
二.填空题(共6小题)
9.如图,写出一个能判定EC∥AB的条件是 .
10.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
11.(多选)下列说法中,错误的有 .
A.两点确定一条直线
B.两条直线被第三条直线所截,同位角相等
C.相等的两个角是对顶角
D.平面内的一条直线和两条平行线中的一条垂直,则它与另一条也垂直
E.从直线外一点到这条直线的垂线段,叫做这点到直线的距离
12.如图,∠BAF=46°,∠ACE=136°.CE⊥CD,则CD与AB 平行(填“是”或“否”)
13.如图,下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角,其中正确的是 (只填序号).
14.如图,直线a和直线b被直线c所截,给出下列条件:
①∠1=∠2; ②∠3=∠6;
③∠4+∠7=180°;④∠5=∠8.
其中不能判断a∥b的条件的序号是 .
三.解答题(共6小题)
15.如图,已知BE平分∠ABD,DE平分∠CDB,且∠1与∠2互余,求证:AB∥CD.
16.如图,点C在∠AOB的平分线OP上,点D在OA上,且∠DOC=∠DCO.DC与OB有怎样的位置关系?为什么?
17.根据图形填空:
(1)若直线ED、BC被直线AB所截,则∠1和 是同位角;
(2)若直线ED、BC被直线AF所截,则∠3和 是内错角;
(3)∠1和∠3是直线AB、AF被直线 所截构成的内错角.
(4)∠2和∠4是直线AB、 被直线BC所截构成的 角.
18.如图,直线MN分别交AB和CD于点E、F,点Q在PM上,∠EPM=∠FQM,且∠AEP=∠CFQ,求证:AB∥CD.
19.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.
20.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
参考答案
一.选择题(共8小题)
1.【解答】解:内错角有:∠1和∠2,∠3和∠4,∠3和∠ABF,∠1和∠11,∠7和∠6,
∠5和∠6,∠4和∠10,∠7和∠8,∠9和∠8,∠10和∠CBH,
共10对,
故选:D.
2.【解答】解:∠1和∠2是直线b和直线c被直线a所截得到的同位角,
故选:D.
3.【解答】解:A、∵∠1=∠4,∴AB∥CD(内错角相等,两直线平行),但不能判定AD∥BC;
B、∵∠3=∠4,∴AD∥BC(同位角相等,两直线平行);
C、∵∠2+∠3=180°,∴AD∥BC(同旁内角互补,两直线平行);
D、∵∠1+∠D=180°,∴AD∥BC(同旁内角互补,两直线平行);
故选:A.
4.【解答】解:①由∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③由∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:D.
5.【解答】解:当∠1=∠2时,AB∥CD,
此时,∠5=∠6,故B选项正确,
而AD与BC不一定平行,AD与DC不一定相等,故A,C,D选项错误;
故选:B.
6.【解答】解:A.∠1与∠A是AE,DE被AD所截而成的同旁内角,正确;
B.∠3与∠A不是同位角,错误;
C.∠2与∠3是DE,AE被BC所截而成的同位角,正确;
D.∠3与∠B是BD,DE被BC所截而成的内错角,正确;
故选:B.
7.【解答】解:A、∠2=∠3,则AB∥DC,故选项错误;
B、∠1=∠4,则AD∥CB,故选项正确;
C、∠1=∠2,不能判定,故选项错误;
D、∠3=∠4,不能判定,故选项错误.
故选:B.
8.【解答】解:A、∵∠1=∠2,∴a∥b,(内错角相等,两直线平行),
故正确;
B、∵∠1=∠2且∠3=∠4,由图可知∠1+∠2=180°,∠3+∠4=180°,
∴∠1=∠2=∠3=∠4=90°,
∴a∥b(内错角相等,两直线平行),
故正确;
C、测得∠1=∠2,且∠3=∠4
∵∠1与∠2,∠3=∠4,即不是内错角也不是同位角,
∴不一定能判定两直线平行,
故错误;
D、∵∠1+∠2=180°,∴a∥b,(同旁内角互补,两直线平行),
故正确.
故选:C.
二.填空题(共6小题)
9.【解答】解:∵∠A=∠ACE,
∴EC∥AB(内错角相等,两直线平行).
故答案为:∠A=∠ACE(答案不唯一).
10.【解答】解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
11.【解答】解:A.两点确定一条直线,故本选项正确;
B.两条平行直线被第三条直线所截,同位角相等,故本选项错误;
C.相等的两个角不一定是对顶角,故本选项错误;
D.平面内的一条直线和两条平行线中的一条垂直,则它与另一条也垂直,故本选项正确;
E.从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故本选项错误;
故答案为:BCE.
12.【解答】解:CD∥AB.
证明:∵CE⊥CD,
∴∠DCE=90°,
∵∠ACE=136°,
∴∠ACD=360°﹣136°﹣90°=134°,
∵∠BAF=46°,
∴∠BAC=180°﹣∠BAF=180°﹣46°=134°,
∴∠ACD=∠BAC,
∴CD∥AB,
故答案为:是.
13.【解答】解:∠2与∠3是直线AB、直线BC,被直线CD所截的一对内错角,因此①符合题意;
∠2与∠B是直线CD、直线BC,被直线AB所截的一对同位角,因此②符合题意;
∠A与∠B是直线AC、直线BC,被直线AB所截的一对同旁内角,因此③符合题意,
∠A与∠ACB是直线AB、直线BC,被直线AC所截的一对同旁内角,因此④不符合题意,
故答案为:①②③.
14.【解答】解:①∠1=∠2可根据同位角相等,两直线平行得到a∥b;
②∠3=∠6可根据内错角相等,两直线平行得到a∥b;
③∠4+∠7=180°可得∠6+∠7=180°根据同旁内角互补,两直线平行得到a∥b;
④∠5=∠8不能判定a∥b;
故答案为:④.
三.解答题(共6小题)
15.【解答】证明:∵∠1与∠2互余,
∴∠1+∠2=90°.
∵BE平分∠ABD,DE平分∠CDB,
∴∠ABD=2∠1,∠BDC=2∠2.
∴∠ABD+∠BDC=2∠1+2∠2=2(∠1+∠2)=180°.
∴AB∥DC.
16.【解答】解:DC与OB的位置关系是互相平行,
∵点C在∠AOB的平分线OP上,
∴∠DOC=∠COB,
∵∠DOC=∠DCO,
∴∠DCO=∠COB,
∴DC∥OB.
17.【解答】解:(1)如图:若ED,BC被AB所截,则∠1与∠2是同位角,
(2)若ED,BC被AF所截,则∠3与∠4是内错角,
(3)∠1 与∠3是AB和AF被ED所截构成的内错角,
(4)∠2与∠4是AB和AF被BC所截构成的同位角.
故答案是:(1)∠2.(2)∠4.(3)ED.(4)AF;同位.
18.【解答】解:如图,
∵∠EPM=∠FQM,∠AEP=∠CFQ,∠EPM+∠AEP+∠1=180°,∠FQM+∠CFQ+∠2=180°,
∴∠1=∠2,
∴AB∥CD.
19.【解答】证明:∵∠1=55°(已知),
∴∠CNM=55°(对顶角相等),
∵∠2=125°(已知),
∴∠CNM+∠2=180°(等式的性质),
∴AB∥CD(同旁内角互补,两直线平行).
20.【解答】解:(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有6对同旁内角.
(3)平面内四条直线两两相交,最多可以形成24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
