沪教版七年级下册:三角形角度计算之八字型与飞镖模型(28张PPT)
文档属性
| 名称 | 沪教版七年级下册:三角形角度计算之八字型与飞镖模型(28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 538.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 08:27:14 | ||
图片预览

文档简介
(共28张PPT)
8字型与飞镖模型
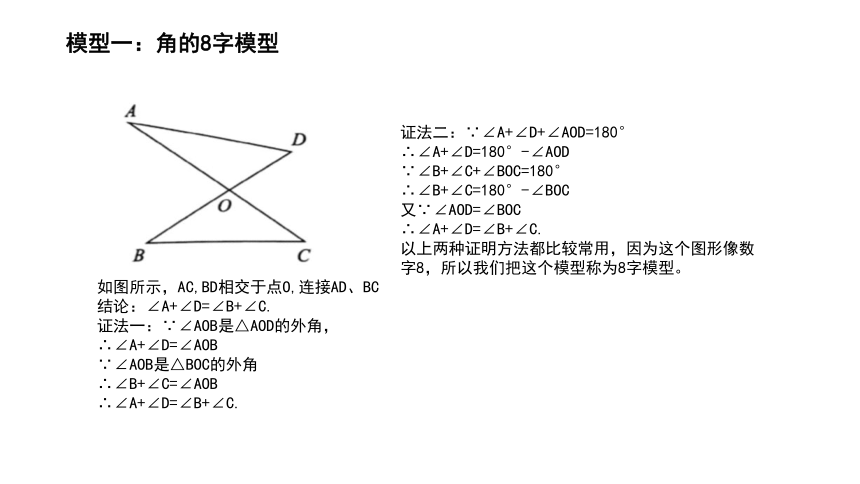
模型一:角的8字模型
如图所示,AC,BD相交于点O,连接AD、BC
结论:∠A+∠D=∠B+∠C.
证法一:∵∠AOB是△AOD的外角,
∴∠A+∠D=∠AOB
∵∠AOB是△BOC的外角
∴∠B+∠C=∠AOB
∴∠A+∠D=∠B+∠C.
证法二:∵∠A+∠D+∠AOD=180°
∴∠A+∠D=180°-∠AOD
∵∠B+∠C+∠BOC=180°
∴∠B+∠C=180°-∠BOC
又∵∠AOD=∠BOC
∴∠A+∠D=∠B+∠C.
以上两种证明方法都比较常用,因为这个图形像数字8,所以我们把这个模型称为8字模型。
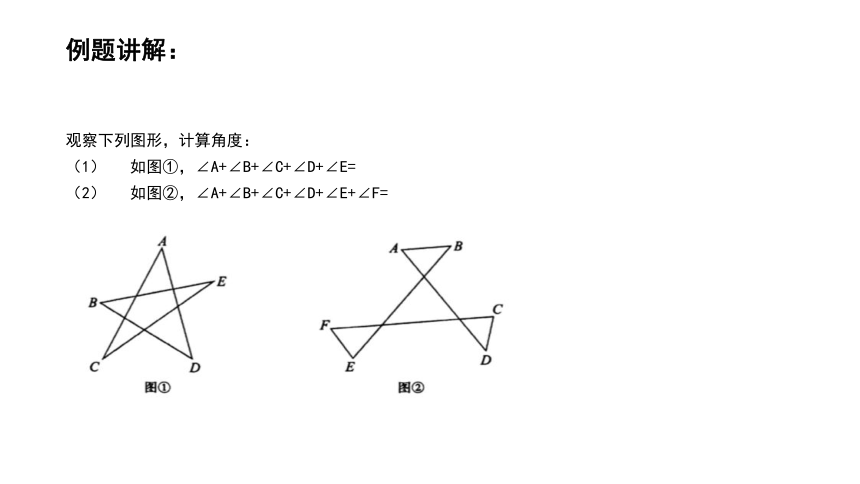
例题讲解:
观察下列图形,计算角度:
(1) 如图①,∠A+∠B+∠C+∠D+∠E=
(2) 如图②,∠A+∠B+∠C+∠D+∠E+∠F=
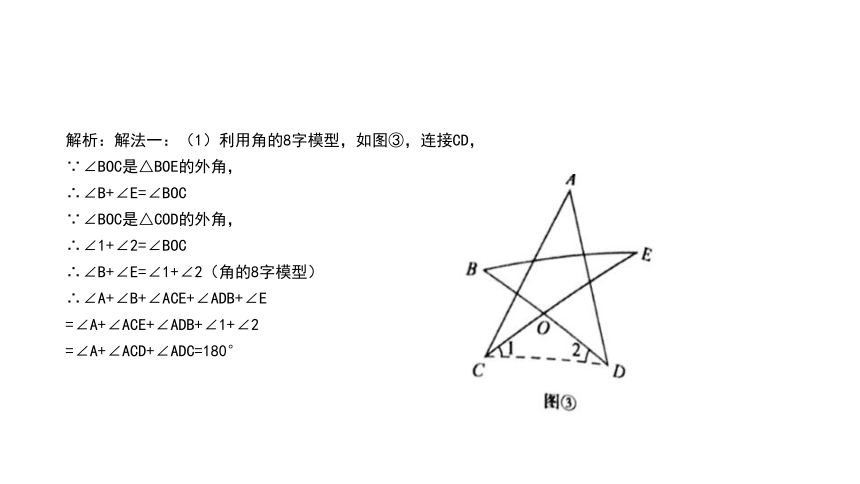
解析:解法一:(1)利用角的8字模型,如图③,连接CD,
∵∠BOC是△BOE的外角,
∴∠B+∠E=∠BOC
∵∠BOC是△COD的外角,
∴∠1+∠2=∠BOC
∴∠B+∠E=∠1+∠2(角的8字模型)
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2
=∠A+∠ACD+∠ADC=180°
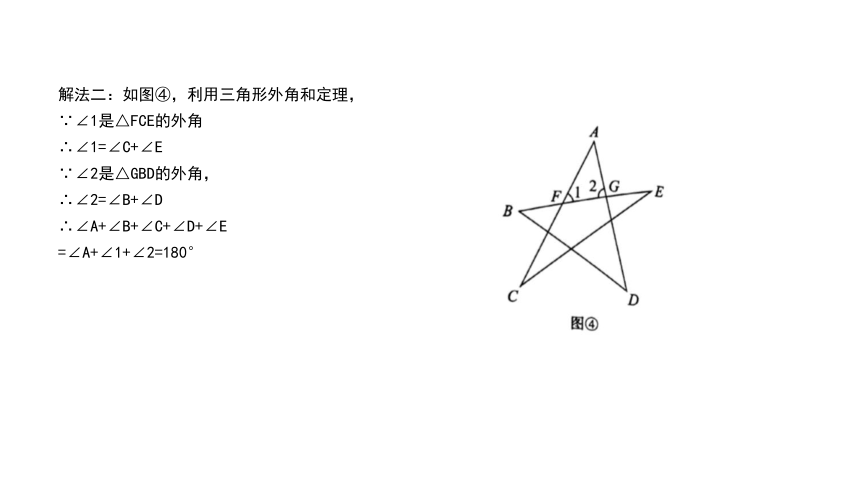
解法二:如图④,利用三角形外角和定理,
∵∠1是△FCE的外角
∴∠1=∠C+∠E
∵∠2是△GBD的外角,
∴∠2=∠B+∠D
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠1+∠2=180°
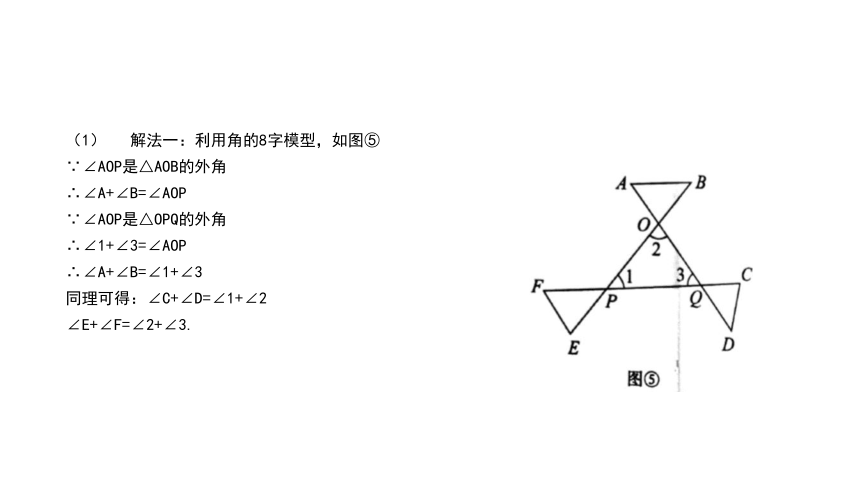
(1) 解法一:利用角的8字模型,如图⑤
∵∠AOP是△AOB的外角
∴∠A+∠B=∠AOP
∵∠AOP是△OPQ的外角
∴∠1+∠3=∠AOP
∴∠A+∠B=∠1+∠3
同理可得:∠C+∠D=∠1+∠2
∠E+∠F=∠2+∠3.
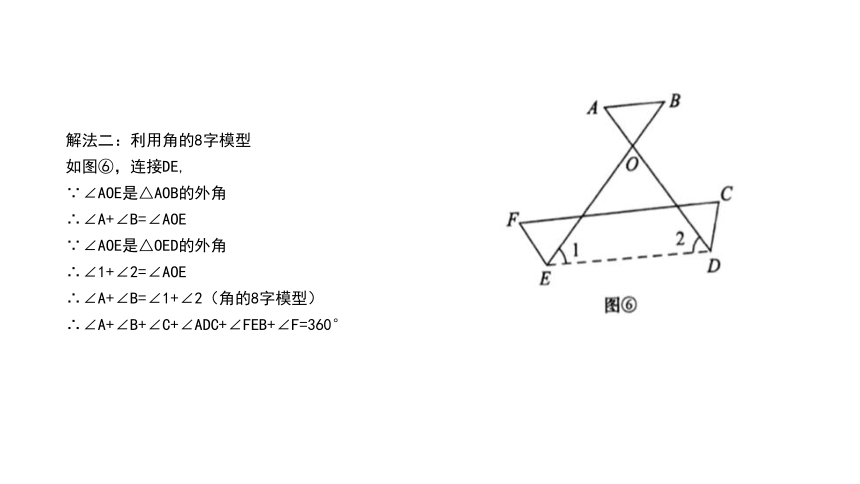
解法二:利用角的8字模型
如图⑥,连接DE,
∵∠AOE是△AOB的外角
∴∠A+∠B=∠AOE
∵∠AOE是△OED的外角
∴∠1+∠2=∠AOE
∴∠A+∠B=∠1+∠2(角的8字模型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F=360°
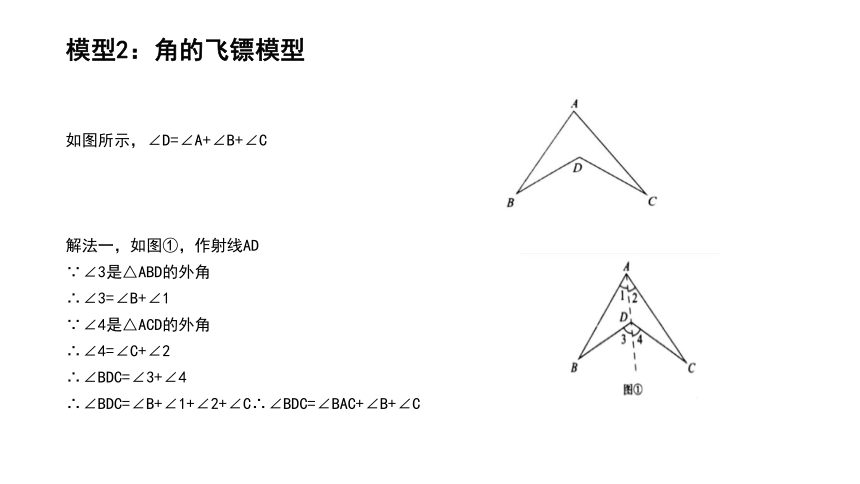
模型2:角的飞镖模型
如图所示,∠D=∠A+∠B+∠C
解法一,如图①,作射线AD
∵∠3是△ABD的外角
∴∠3=∠B+∠1
∵∠4是△ACD的外角
∴∠4=∠C+∠2
∴∠BDC=∠3+∠4
∴∠BDC=∠B+∠1+∠2+∠C∴∠BDC=∠BAC+∠B+∠C
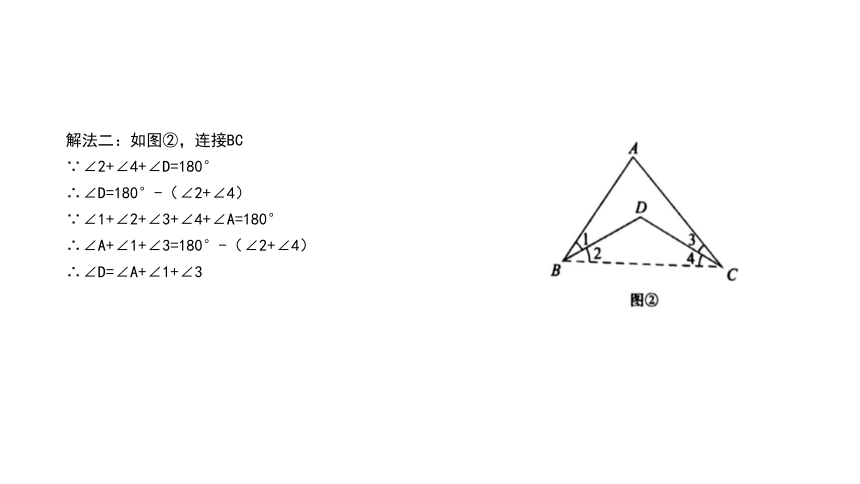
解法二:如图②,连接BC
∵∠2+∠4+∠D=180°
∴∠D=180°-(∠2+∠4)
∵∠1+∠2+∠3+∠4+∠A=180°
∴∠A+∠1+∠3=180°-(∠2+∠4)
∴∠D=∠A+∠1+∠3
例题讲解:
如图,在四边形ABCD中,AM,CM分别平分∠DAB和∠DCB,AM与CM交于M,探究∠AMC与∠B∠D之间的数量关系.
利用角的飞镖模型
如图所示,连接DM并延长,
∵∠3是△AMD的外角,
∴∠3=∠1+∠ADM
∵∠4是△CMD的外角
∴∠4=∠2+∠CDM
∵∠AMC=∠3+∠4
∴∠AMC=∠1+∠ADM+∠CDM+∠2
∴∠AMC=∠1+∠2+∠ADC(角的飞镖模型)|
利用四边形的内角和,以及AM,CM分别平分∠DAB和∠DCB就可以得出2∠AMC+∠B-∠ADC=360°.
模型三:边的8字模型
如图所示,AC,BD相交于点O
连接AD,BC结论:AC+BD>AD+BC
模型分析:
∵OA+OD>AD
OB+OC>BC
以上两式进行相加即可得到
OA+OD+OB+OC>BC+AD
即AC+BD>AD+BC
例题讲解:
如图,四边形ABCD的对角线AC,BD相交于点O
求证:(1)AB+BC+CD+AD>AC+BD
(2)AB+BC+CD+AD<2AC+2BD.
解析:(1)∵AB+BC>AC
CD+AD>AC
AB+AD>BD
BC+CD>BD
以上式子相加即可得到AB+BC+CD+AD>AC+BD
(2)∵AD<OA+OD
BC<OB+OC
两式相加即可得到AD+BC<OA+OD+OB+OC
∴AD+BC<AC+BD(边的8字模型)
同理可证:AB+CD<AC+BD
∴AB+BC+CD+AD<2AC+2BD
模型四:边的飞镖模型
如图所示,AB+AC>BD+CD
解析:如图,延长BD交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC
∵BE+EC=BD+DE+EC
DE+EC>CD
∴BE+EC>BD+CD
综上:AB+AC>BD+CD
经典例题练习:
1、 如图1,求:∠CAD+∠B+∠C+∠D+∠E=
如图2,求:∠CAD+∠B+∠AC+∠D+∠E=
解析:
如图,连接DE
∠C+∠CAD=∠1+∠2
∠CAD+∠B+∠C+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
如图,连接DE
∠ACE+∠CAD=∠1+∠2
∠CAD+∠B+∠ACE+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
1、如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
解析:如图,连接GH,CD
∠E+∠B=∠1+∠2
∠A+∠F=∠3+∠4
∠A+∠B+∠FCH+∠ADG+∠E+∠F+∠DGB+∠EHC
=∠1+∠2+∠3+∠4+∠GDA+∠FCH+∠DGB+∠EHC=360°
如图,求∠A+∠B+∠C+∠D+∠E+∠F=
解析:
∠C+∠E+∠D=∠EOC=115°
∠A+∠B+∠F=∠BOF=115°
∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°
如图,求∠A+∠B+∠C+∠D=
解析:如图所示,连接BD
∠AED=∠A+∠3+∠1
∠BFC=∠2+∠4+∠C
∠A+∠ABF+∠C+∠CDE
=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220°
4、 如图,点O为△ABC内部一点
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO
解析:(1)∵OA+OB>AB ①
OB+OC>BC ②
OC+OA>AC ③
由①+②+③可得
2(AO+BO+CO)>AB+BC+AC;
(2)如图,延长BO交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC ①
∵BE+EC=BO+OE+EC
OE+EC>CO
∴BE+EC>BO+CO ②
由①②可得AB+AC>BO+CO ③(边的飞镖模型)
同理可得AB+BCD>OA+OC④
BC+AC>OA+OB⑤
由③+④+⑤得AB+BC+AC>AO+BO+CO
如图,在△ABC中,D、E在BC边上,且BD=CE,求证:AB+AC>AD+AE
解析:如图,将AC平移至BF,AD延长线于BF相交于点G,连接DF
由平移可得AC=BF
∵AC∥BF
∴∠ACE=∠FBD
∵BD=CE
∴△AEC≌△FDB
∴DF=AE
如图,延长AD交BF于点G
∵AB+BF=AB+BG+GF
∵AB+BG>AG
∴AB+BF>AG+GF ①
∵AG+GF=AD+DG+GF
∵DG+GF>DF
∴AG+GF>AD+DF ②
由①②可得
AB+AC=AB+BF>AD+DF=AD+AE
∴AB+AC>AD+AE.
8字型与飞镖模型
模型一:角的8字模型
如图所示,AC,BD相交于点O,连接AD、BC
结论:∠A+∠D=∠B+∠C.
证法一:∵∠AOB是△AOD的外角,
∴∠A+∠D=∠AOB
∵∠AOB是△BOC的外角
∴∠B+∠C=∠AOB
∴∠A+∠D=∠B+∠C.
证法二:∵∠A+∠D+∠AOD=180°
∴∠A+∠D=180°-∠AOD
∵∠B+∠C+∠BOC=180°
∴∠B+∠C=180°-∠BOC
又∵∠AOD=∠BOC
∴∠A+∠D=∠B+∠C.
以上两种证明方法都比较常用,因为这个图形像数字8,所以我们把这个模型称为8字模型。
例题讲解:
观察下列图形,计算角度:
(1) 如图①,∠A+∠B+∠C+∠D+∠E=
(2) 如图②,∠A+∠B+∠C+∠D+∠E+∠F=
解析:解法一:(1)利用角的8字模型,如图③,连接CD,
∵∠BOC是△BOE的外角,
∴∠B+∠E=∠BOC
∵∠BOC是△COD的外角,
∴∠1+∠2=∠BOC
∴∠B+∠E=∠1+∠2(角的8字模型)
∴∠A+∠B+∠ACE+∠ADB+∠E
=∠A+∠ACE+∠ADB+∠1+∠2
=∠A+∠ACD+∠ADC=180°
解法二:如图④,利用三角形外角和定理,
∵∠1是△FCE的外角
∴∠1=∠C+∠E
∵∠2是△GBD的外角,
∴∠2=∠B+∠D
∴∠A+∠B+∠C+∠D+∠E
=∠A+∠1+∠2=180°
(1) 解法一:利用角的8字模型,如图⑤
∵∠AOP是△AOB的外角
∴∠A+∠B=∠AOP
∵∠AOP是△OPQ的外角
∴∠1+∠3=∠AOP
∴∠A+∠B=∠1+∠3
同理可得:∠C+∠D=∠1+∠2
∠E+∠F=∠2+∠3.
解法二:利用角的8字模型
如图⑥,连接DE,
∵∠AOE是△AOB的外角
∴∠A+∠B=∠AOE
∵∠AOE是△OED的外角
∴∠1+∠2=∠AOE
∴∠A+∠B=∠1+∠2(角的8字模型)
∴∠A+∠B+∠C+∠ADC+∠FEB+∠F=360°
模型2:角的飞镖模型
如图所示,∠D=∠A+∠B+∠C
解法一,如图①,作射线AD
∵∠3是△ABD的外角
∴∠3=∠B+∠1
∵∠4是△ACD的外角
∴∠4=∠C+∠2
∴∠BDC=∠3+∠4
∴∠BDC=∠B+∠1+∠2+∠C∴∠BDC=∠BAC+∠B+∠C
解法二:如图②,连接BC
∵∠2+∠4+∠D=180°
∴∠D=180°-(∠2+∠4)
∵∠1+∠2+∠3+∠4+∠A=180°
∴∠A+∠1+∠3=180°-(∠2+∠4)
∴∠D=∠A+∠1+∠3
例题讲解:
如图,在四边形ABCD中,AM,CM分别平分∠DAB和∠DCB,AM与CM交于M,探究∠AMC与∠B∠D之间的数量关系.
利用角的飞镖模型
如图所示,连接DM并延长,
∵∠3是△AMD的外角,
∴∠3=∠1+∠ADM
∵∠4是△CMD的外角
∴∠4=∠2+∠CDM
∵∠AMC=∠3+∠4
∴∠AMC=∠1+∠ADM+∠CDM+∠2
∴∠AMC=∠1+∠2+∠ADC(角的飞镖模型)|
利用四边形的内角和,以及AM,CM分别平分∠DAB和∠DCB就可以得出2∠AMC+∠B-∠ADC=360°.
模型三:边的8字模型
如图所示,AC,BD相交于点O
连接AD,BC结论:AC+BD>AD+BC
模型分析:
∵OA+OD>AD
OB+OC>BC
以上两式进行相加即可得到
OA+OD+OB+OC>BC+AD
即AC+BD>AD+BC
例题讲解:
如图,四边形ABCD的对角线AC,BD相交于点O
求证:(1)AB+BC+CD+AD>AC+BD
(2)AB+BC+CD+AD<2AC+2BD.
解析:(1)∵AB+BC>AC
CD+AD>AC
AB+AD>BD
BC+CD>BD
以上式子相加即可得到AB+BC+CD+AD>AC+BD
(2)∵AD<OA+OD
BC<OB+OC
两式相加即可得到AD+BC<OA+OD+OB+OC
∴AD+BC<AC+BD(边的8字模型)
同理可证:AB+CD<AC+BD
∴AB+BC+CD+AD<2AC+2BD
模型四:边的飞镖模型
如图所示,AB+AC>BD+CD
解析:如图,延长BD交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC
∵BE+EC=BD+DE+EC
DE+EC>CD
∴BE+EC>BD+CD
综上:AB+AC>BD+CD
经典例题练习:
1、 如图1,求:∠CAD+∠B+∠C+∠D+∠E=
如图2,求:∠CAD+∠B+∠AC+∠D+∠E=
解析:
如图,连接DE
∠C+∠CAD=∠1+∠2
∠CAD+∠B+∠C+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
如图,连接DE
∠ACE+∠CAD=∠1+∠2
∠CAD+∠B+∠ACE+∠ADB+∠BEC=∠B+∠BEC+∠BDA+∠1+∠2=180°
1、如图,求:∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
解析:如图,连接GH,CD
∠E+∠B=∠1+∠2
∠A+∠F=∠3+∠4
∠A+∠B+∠FCH+∠ADG+∠E+∠F+∠DGB+∠EHC
=∠1+∠2+∠3+∠4+∠GDA+∠FCH+∠DGB+∠EHC=360°
如图,求∠A+∠B+∠C+∠D+∠E+∠F=
解析:
∠C+∠E+∠D=∠EOC=115°
∠A+∠B+∠F=∠BOF=115°
∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°
如图,求∠A+∠B+∠C+∠D=
解析:如图所示,连接BD
∠AED=∠A+∠3+∠1
∠BFC=∠2+∠4+∠C
∠A+∠ABF+∠C+∠CDE
=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220°
4、 如图,点O为△ABC内部一点
求证:(1)2(AO+BO+CO)>AB+BC+AC;
(2)AB+BC+AC>AO+BO+CO
解析:(1)∵OA+OB>AB ①
OB+OC>BC ②
OC+OA>AC ③
由①+②+③可得
2(AO+BO+CO)>AB+BC+AC;
(2)如图,延长BO交AC于点E
∵AB+AC=AB+AE+EC
AB+AE>BE
∴AB+AC>BE+EC ①
∵BE+EC=BO+OE+EC
OE+EC>CO
∴BE+EC>BO+CO ②
由①②可得AB+AC>BO+CO ③(边的飞镖模型)
同理可得AB+BCD>OA+OC④
BC+AC>OA+OB⑤
由③+④+⑤得AB+BC+AC>AO+BO+CO
如图,在△ABC中,D、E在BC边上,且BD=CE,求证:AB+AC>AD+AE
解析:如图,将AC平移至BF,AD延长线于BF相交于点G,连接DF
由平移可得AC=BF
∵AC∥BF
∴∠ACE=∠FBD
∵BD=CE
∴△AEC≌△FDB
∴DF=AE
如图,延长AD交BF于点G
∵AB+BF=AB+BG+GF
∵AB+BG>AG
∴AB+BF>AG+GF ①
∵AG+GF=AD+DG+GF
∵DG+GF>DF
∴AG+GF>AD+DF ②
由①②可得
AB+AC=AB+BF>AD+DF=AD+AE
∴AB+AC>AD+AE.
