人教版七年级下册数学7.1.2-平面直角坐标系课件(3课时 共54张)
文档属性
| 名称 | 人教版七年级下册数学7.1.2-平面直角坐标系课件(3课时 共54张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 21:23:18 | ||
图片预览





文档简介
(共54张PPT)
平面直角坐标系
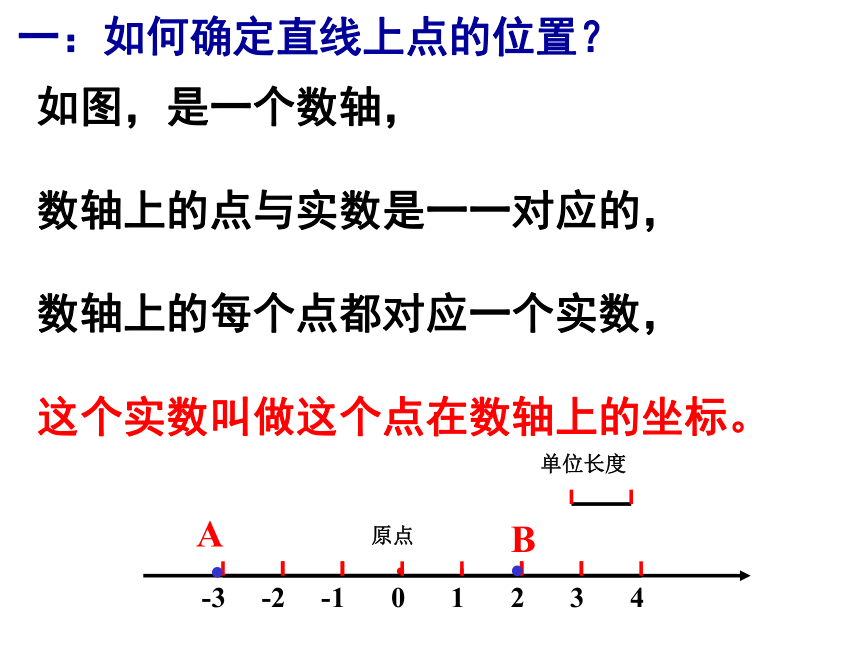
一:如何确定直线上点的位置?
如图,是一个数轴,
数轴上的点与实数是一一对应的,
数轴上的每个点都对应一个实数,
这个实数叫做这个点在数轴上的坐标。
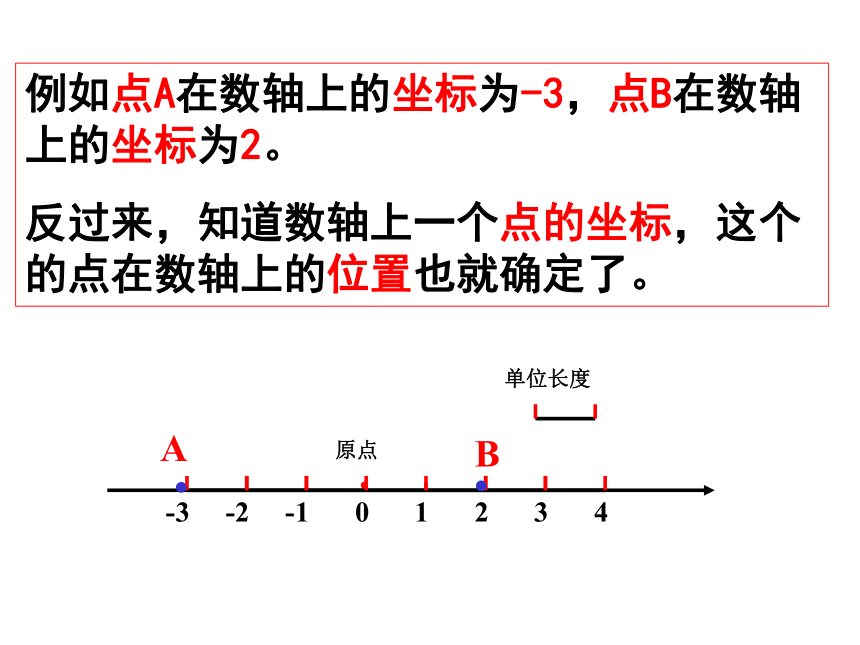
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。
反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
类似于利用数轴确定直线上的点的位置的
方法,能否找到一种方法来确定平面内的
点的位置呢? (点A,B,C,D.)
?
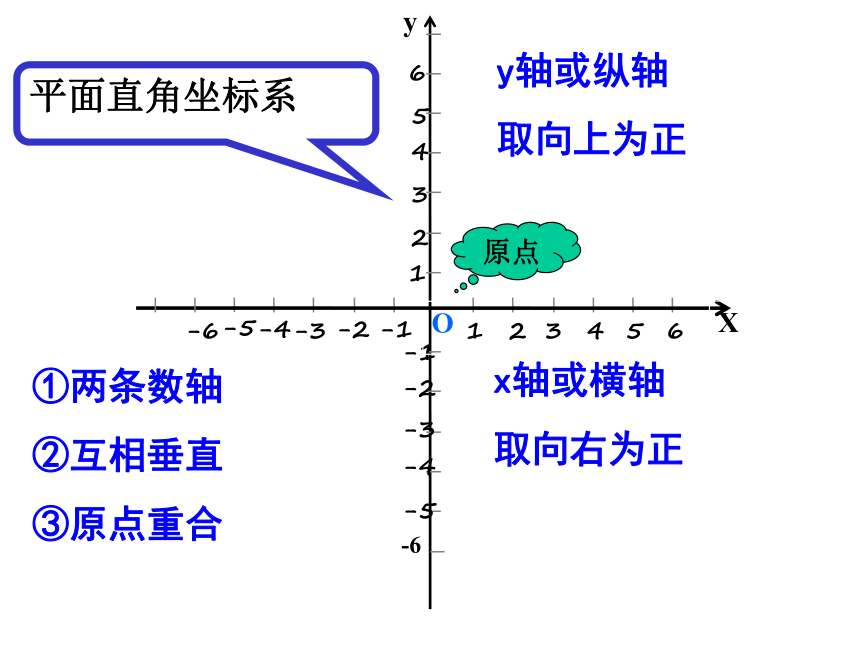
二:平面上确定一个点的位置的方法
O
x轴或横轴
取向右为正
y轴或纵轴
取向上为正
原点
①两条数轴
②互相垂直
③原点重合
平面直角坐标系
平面直角坐标系概念:
平面内两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平方向的数轴称为x轴或横轴,习惯取向右的方向为正方向,
竖直方向上的数轴称为y轴或纵轴,习惯取向上的方向为正方向;
两坐标轴的交点是平面直角坐标系的原点.
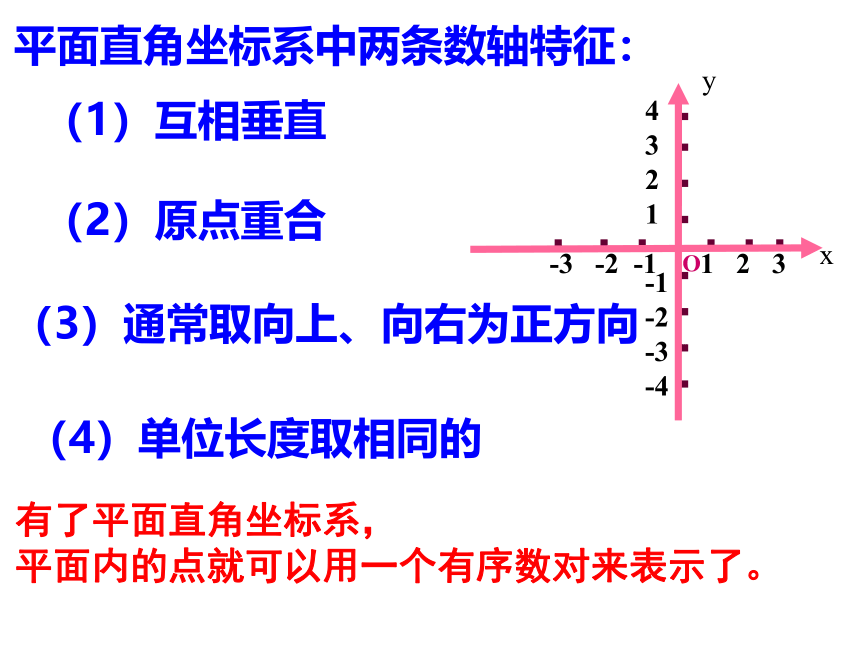
平面直角坐标系中两条数轴特征:
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度取相同的
O
x
y
-3 -2 -1 1 2 3
4
3
2
1
-1
-2
-3
-4
有了平面直角坐标系,
平面内的点就可以用一个有序数对来表示了。
X
O
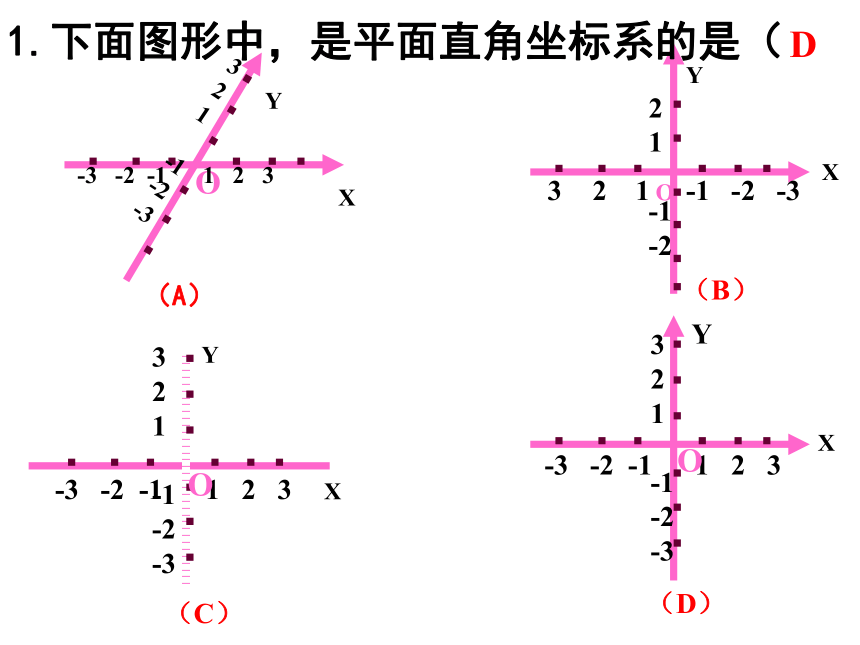
1.下面图形中,是平面直角坐标系的是( )
X
X
Y
(A)
3 2 1 -1 -2 -3
X
Y
(B)
2
1
-1
-2
O
D
2.平面上__________________组成平面直角
坐标系,_________叫x轴(横轴),取向
____为正方向,____________叫y轴(纵轴),
取向___为正方向。
两坐标轴的交点是平面直角坐标系的_______。
水平的数轴
右
上
竖直的数轴
原点
互相垂直,原点重合的两条直线
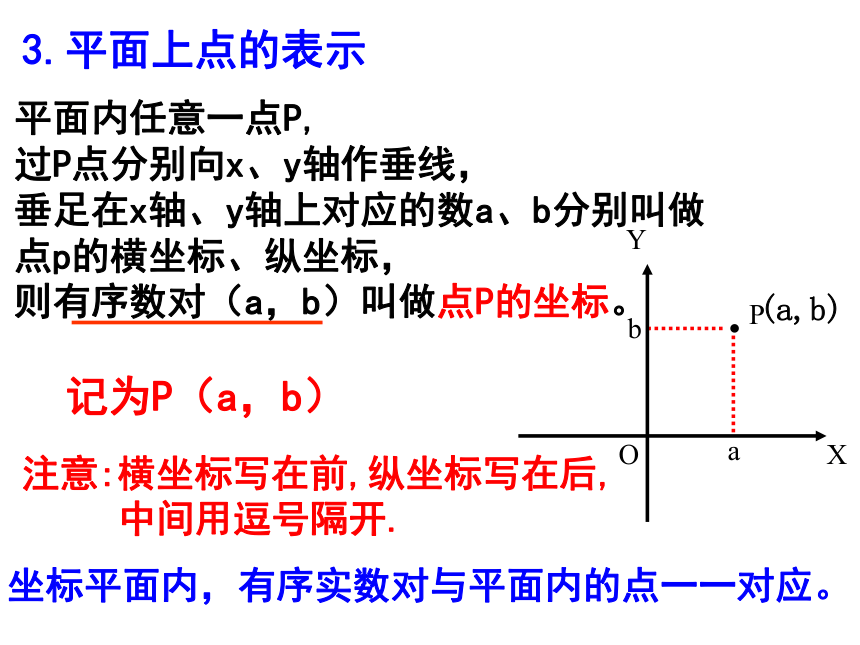
3.平面上点的表示
平面内任意一点P,
过P点分别向x、y轴作垂线,
垂足在x轴、y轴上对应的数a、b分别叫做
点p的横坐标、纵坐标,
则有序数对(a,b)叫做点P的坐标。
a
b
记为P(a,b)
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
坐标平面内,有序实数对与平面内的点一一对应。
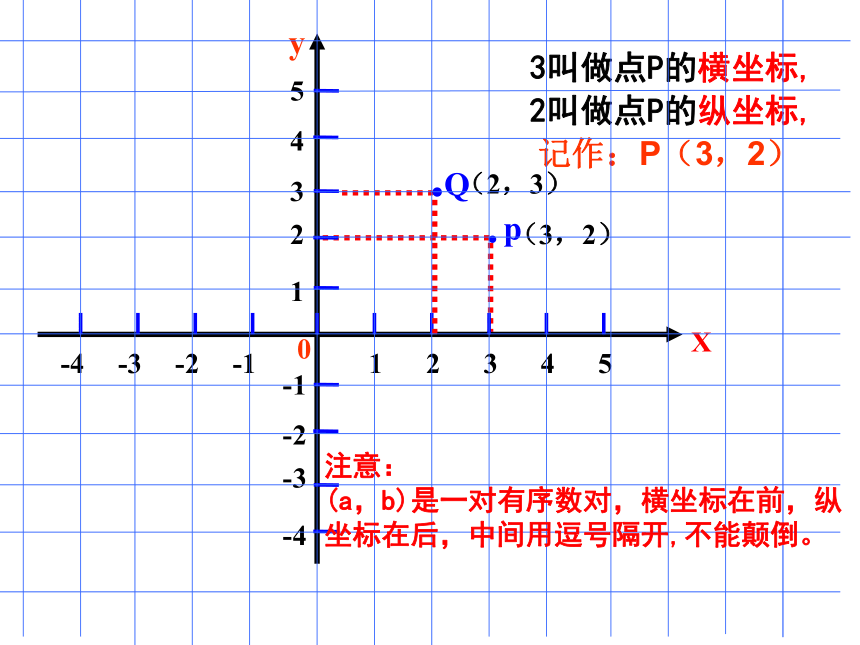
(3,2)
p
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
X
记作:P(3,2)
·
(2,3)
注意:
(a,b)是一对有序数对,横坐标在前,纵
坐标在后,中间用逗号隔开,不能颠倒。
·
B
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
例1 写出图中A、B、C、D、E各点的坐标。
·
(2,-3)
例2.在平面直角坐标系中描出下列各点, A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)
A
(0,5)
(5,2)
(-2,-3)
·
-2
-3
o
-1
1
例3.在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
思考:
点A(5,2)到Ax轴的距离是多少?到y轴距离是多少?
点B(-3,-4)到Ax轴距离是多少?到y轴距离是多少?
你发现了什么?
A
(5,2)
(-2,-3)
小结:
点P(x,y)到x轴的距离为 ,
到y轴的距离为 。
因为距离是非负数,所以要加绝对值符号。
练习:
点 M(- 8,12)到x轴的距离是_______,
到y轴的距离是______ .
思考:
原点0的坐标是什么?
坐标轴上的点有什么特征?
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
坐标轴上点有何特征?
在x轴上的点,
纵坐标等于0.
在y轴上的点,
横坐标等于0.
①y轴上的点横坐标为0,
纵坐标为任意实数.
②x轴上的点纵坐标为0,
横坐标为任意实数。
坐标轴上的点有何特征?
小结:
1)原点0的坐标为______.
2)坐标轴上的点P(a,b)坐标的特征:
①点P在x轴上,则b_____,a______;
②点P在y轴上,则a_____,b_______。
练习:
1.(9,0)在____轴上,(-3,0)在_____轴上。
2..在y轴上的点的横坐标是______,
在x轴上的点的纵坐标是_______.
练习:
1.对于平面内任意一点P,过点P分别向x轴、
y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点p的_____、_______,则有序数对(a,b)叫做点P的______。
2. 坐标平面内,有序实数对与平面内的点___.
3.点P(-a,b)到x轴的距离为_____,
到y轴的距离为______。
4.在x轴上的点的坐标特征:
横坐标___,纵坐标_____;
在y轴上的点的坐标特征:
横坐标___,纵坐标_____.
5.点P(x,y)的坐标满足xy=0,则点P的位置是______.
第2课时
象 限
5
-2
-3
-4
-1
3
2
4
1
6
y
第一象限
第二象限
第三象限
第四象限
象限:
两条坐标轴把平面分成如图所示的四个部分.
注意:坐标轴上的点不属于任何象限。
x
y
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
观察:各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
注意:坐标轴上的点不属于任何象限。
四个象限内点的特点:
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
直角坐标系中点的坐标的特点
—
+
—
—
+
—
—
—
+
+
0
0
0
0
0
0
考考你:
1. 请你根据下列各点的坐标判定它们分别在第几
象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0),G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
2.在平面直角坐标系内,下列各点在第四象
限的是( )
A.(2,1) B.(-2,1)
C.(-3,-5) D.(3,-5)
3.已知坐标平面内点A(m,n)在第四象限,那
么点B(n,m)在( )
A.第一象限 B.第二象限.
C.第三象限 D.第四象限
D
B
4.若 <0,那么a(x,y)在第___象限。
5.点P(a,b)在第四象限,则a__0,b__0.
6.设M(a,b)为平面直角坐标系中的点。
①当a>0,b<0,点M在第几象限?
②当ab<0,点M位于第几象限?
③当a为任意实数,且b<0时,点M位于何处?
(纵坐标为b<0,说明点M位于x轴下方,
可以是y轴负半轴,第三或四象限。)
7.若a<0,则点P(-a,2)应在第___象限。
8.若点M(a+b,ab)在第三象限,则点N(a,b)
在第___象限。
9.在平面直角坐标系内,在第二象限内有一点P,且P到x轴的距离为3,到y轴的距离是5,则P点坐标为____.
10.在平面直角坐标系内第二象限内有一点A,且A
到x轴的距离为3,到y轴的距离是到x轴距离的3
倍,则A点坐标为____.
11.点M位于x轴下方,距x轴3个单位长,且位于y轴
左侧,距y轴2个单位长,则M点的坐标是____.
12.在平面直角坐标系中,点P的坐标为(-2,a?+1)
则点P所在象限是第____象限。
13.已知点P坐标为(2-a,3a+6)且点P到两坐
标轴的距离相等,则点P的坐标是( )
A.(3,3) B.(3,-3 )
C.(6,-6) D.(3,3)或(6,-6)
14.点A在x轴上,距离原点4个单位长度,
则A点的坐标是 ___________。
15.如果B(m+1,3m-5)到x轴的距离为它到y
轴距离相等,求m的值。
(4,0)或(-4,0)
第3课时
坐标特点
·
-2
-3
o
-1
1
·
·
·
·
·
·
-4
-1
4
(-4,3)
(4,3)
(-2,3)
(2,3)
(-2,-3)
(2,-3)
·
观察直角坐标系中下列各点.你能发现什么?
B
C
D
E
F
G
小结:
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
练习:
1.平行于横轴的直线上的点的_______相同;
平行于纵轴的直线上的点的_______相同;
2.已知平面直角坐标系内两点M(5,a),N(b,-2).
①若MN∥y轴,则a______,b____.
②若MN∥y轴,则a______,b____.
3.已知点M(3a-2,a+6),点N的坐标为(2,5)且直线MN∥x轴,求点M的坐标。
4.如果直线l∥x轴,且到x轴距离为5,那么直线l与
y轴交点的坐标是___.
5.已知点P1(a-1,5)和P2(2,b-1)到x轴距离相等,且P1P2∥y轴,则(a+b)2015的值为多少?
6.已知点M(3,a),N(b,-1),根据下列条件求a,b
的值。
①M、N两点关于x轴对称
②M、N两点的连线平行于y轴
③M、N两点在第二、四象限的角平分线上。
分别写出图中点A、B、C、D的坐标,
观察图形,并回答问题.
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点A与点B的位置有什么特点?
点A与点B的坐标有什么关系?
点A与点C的位置有什么特点?
点A与点C的坐标有什么关系?
关于x轴对称的点:横坐标相同,纵坐标互为相反数.
关于y轴对称的点:纵坐标相同,横坐标互为相反数.
A
B
C
D
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点B与点C的位置有什么特点?
点B与点C的坐标有什么关系?
关于原点对称的点:横坐标、纵坐标都互为相反数
A
B
C
D
归纳:
平面直角坐标系中的点p(x,y):
关于x轴的对称点是(x,-y);
关于y轴的对称点是(-x,y);
关于原点的对称点是p(-x,-y)。
关于x轴对称的点:横坐标相同,纵坐标互为相反数.
关于y轴对称的点:纵坐标相同,横坐标互为相反数.
关于原点对称的点:横坐标、纵坐标都互为相反数
练习:
1. 平面直角坐标系中的点p(x,y):
关于x轴的对称点是________;
关于y轴的对称点是________;
关于原点的对称点是_______。
2.点A(2,-3)关于x轴对称的点的坐标是____.
3.点B(-2,1)关于y轴对称的点的坐标是____.
4.点(4,3)与点(4,- 3)的关系是( ) . (A)关于原点对称 (B)关于 x轴对称 (C)关于 y轴对称 (D)不能构成对称关系
5.与点P(M,-1)关于原点的对称点是P(2,n),
则m+n的值为_______.
6.若点A(n,2)与B(-3,m)关于原点对称,
则n-m的值为______.
7.在平面直角坐标系中,点P(m?+1,-2)关于x轴对称的点在第___象限;关于y轴对称的点在第____象限。
观察图形,并回答问题.
点B和点C在第二、四象限的角平分线上,
(3,-3)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,3)
0
点B与点C的坐标有什么关系?
B
C
第二、四象限两坐标轴夹角平分线上的点;
的横、纵坐标互为相反数。
观察图形,并回答问题.
点A和点D在第二、四象限的角平分线上,
(2,2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-2,-2)
0
点A与点D的坐标有什么关系?
A
D
第一、三象限两坐标轴夹角平分线上的点
的横、纵坐标相等。
两坐标轴夹角平分线上的点的坐标的特征:
①第一、三象限两坐标轴夹角平分线上的点
的横、纵坐标相等。
②第二、四象限两坐标轴夹角平分线上的点
的横、纵坐标互为相反数。
练习:
1.第一、三象限两坐标轴夹角平分线上的点
的横、纵坐标______。
第二、四象限两坐标轴夹角平分线上的点
的横、纵坐标______。
2.已知点A(a,-2),B(-3,b)根据下列条件
求出a,b的值。
①A、B两点在二、四象限的角平分线上。
②A、B两点在一、三象限的角平分线上。
新题型 :利用坐标求线段长及图形面积
1.已知P(2,5),a(3,-4),则pa的长为( )
2.在直角坐标系中,画出以A(2,0)、B(-3,0)、
C(0,-3)为顶点的三角形,并求出△ABC的面积。
3.已知△ABC三顶点坐标为A(-2,0)、B(4,0)、
C(2,-3),求S△ABC
4.如图,已知A、B坐标分别为A(2,4)、B(4,1)
试求△ABO的面积。
C
你的收获!
平面直角坐标系
一:如何确定直线上点的位置?
如图,是一个数轴,
数轴上的点与实数是一一对应的,
数轴上的每个点都对应一个实数,
这个实数叫做这个点在数轴上的坐标。
例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。
反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
类似于利用数轴确定直线上的点的位置的
方法,能否找到一种方法来确定平面内的
点的位置呢? (点A,B,C,D.)
?
二:平面上确定一个点的位置的方法
O
x轴或横轴
取向右为正
y轴或纵轴
取向上为正
原点
①两条数轴
②互相垂直
③原点重合
平面直角坐标系
平面直角坐标系概念:
平面内两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平方向的数轴称为x轴或横轴,习惯取向右的方向为正方向,
竖直方向上的数轴称为y轴或纵轴,习惯取向上的方向为正方向;
两坐标轴的交点是平面直角坐标系的原点.
平面直角坐标系中两条数轴特征:
(1)互相垂直
(2)原点重合
(3)通常取向上、向右为正方向
(4)单位长度取相同的
O
x
y
-3 -2 -1 1 2 3
4
3
2
1
-1
-2
-3
-4
有了平面直角坐标系,
平面内的点就可以用一个有序数对来表示了。
X
O
1.下面图形中,是平面直角坐标系的是( )
X
X
Y
(A)
3 2 1 -1 -2 -3
X
Y
(B)
2
1
-1
-2
O
D
2.平面上__________________组成平面直角
坐标系,_________叫x轴(横轴),取向
____为正方向,____________叫y轴(纵轴),
取向___为正方向。
两坐标轴的交点是平面直角坐标系的_______。
水平的数轴
右
上
竖直的数轴
原点
互相垂直,原点重合的两条直线
3.平面上点的表示
平面内任意一点P,
过P点分别向x、y轴作垂线,
垂足在x轴、y轴上对应的数a、b分别叫做
点p的横坐标、纵坐标,
则有序数对(a,b)叫做点P的坐标。
a
b
记为P(a,b)
注意:横坐标写在前,纵坐标写在后,
中间用逗号隔开.
(a,b)
坐标平面内,有序实数对与平面内的点一一对应。
(3,2)
p
y
3叫做点P的横坐标,
2叫做点P的纵坐标,
X
记作:P(3,2)
·
(2,3)
注意:
(a,b)是一对有序数对,横坐标在前,纵
坐标在后,中间用逗号隔开,不能颠倒。
·
B
C
·
A
·
E
·
D
( 2,3 )
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
例1 写出图中A、B、C、D、E各点的坐标。
·
(2,-3)
例2.在平面直角坐标系中描出下列各点, A(5,2) 、B(0,5)、C(2,-3)、 D(-2,-3)
A
(0,5)
(5,2)
(-2,-3)
·
-2
-3
o
-1
1
例3.在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
思考:
点A(5,2)到Ax轴的距离是多少?到y轴距离是多少?
点B(-3,-4)到Ax轴距离是多少?到y轴距离是多少?
你发现了什么?
A
(5,2)
(-2,-3)
小结:
点P(x,y)到x轴的距离为 ,
到y轴的距离为 。
因为距离是非负数,所以要加绝对值符号。
练习:
点 M(- 8,12)到x轴的距离是_______,
到y轴的距离是______ .
思考:
原点0的坐标是什么?
坐标轴上的点有什么特征?
A
B
C
D
(3,0)
(-4,0)
(0,5)
(0,-4)
(0,0)
坐标轴上点有何特征?
在x轴上的点,
纵坐标等于0.
在y轴上的点,
横坐标等于0.
①y轴上的点横坐标为0,
纵坐标为任意实数.
②x轴上的点纵坐标为0,
横坐标为任意实数。
坐标轴上的点有何特征?
小结:
1)原点0的坐标为______.
2)坐标轴上的点P(a,b)坐标的特征:
①点P在x轴上,则b_____,a______;
②点P在y轴上,则a_____,b_______。
练习:
1.(9,0)在____轴上,(-3,0)在_____轴上。
2..在y轴上的点的横坐标是______,
在x轴上的点的纵坐标是_______.
练习:
1.对于平面内任意一点P,过点P分别向x轴、
y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点p的_____、_______,则有序数对(a,b)叫做点P的______。
2. 坐标平面内,有序实数对与平面内的点___.
3.点P(-a,b)到x轴的距离为_____,
到y轴的距离为______。
4.在x轴上的点的坐标特征:
横坐标___,纵坐标_____;
在y轴上的点的坐标特征:
横坐标___,纵坐标_____.
5.点P(x,y)的坐标满足xy=0,则点P的位置是______.
第2课时
象 限
5
-2
-3
-4
-1
3
2
4
1
6
y
第一象限
第二象限
第三象限
第四象限
象限:
两条坐标轴把平面分成如图所示的四个部分.
注意:坐标轴上的点不属于任何象限。
x
y
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
x
y
o
-1
2
3
4
5
6
7
8
9
-2
-3
-4
-5
-6
-7
-8
-9
1
1
2
3
4
5
-1
-2
-3
-4
-5
A
B
C
观察:各象限内的点的坐标有何特征?
D
E
(-2,3)
(5,3)
(3,2)
(5,-4)
(-7,-5)
F
G
H
(-7,2)
(-5,-4)
(3,-5)
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
o
X
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
注意:坐标轴上的点不属于任何象限。
四个象限内点的特点:
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
直角坐标系中点的坐标的特点
—
+
—
—
+
—
—
—
+
+
0
0
0
0
0
0
考考你:
1. 请你根据下列各点的坐标判定它们分别在第几
象限或在什么坐标轴上?
A(-5、2) B(3、-2) C(0、4), D(-6、0) E(1、8) F(0、0),G(5、0),H(-6、-4)K(0、-3)
解:A在第二象限,
B在第四象限,
C在Y的正半轴,
E在第一象限,
D在X轴的负半轴,
F在原点,
G在X轴的正半轴,
H在第三象限,
K在Y轴的负半轴。
2.在平面直角坐标系内,下列各点在第四象
限的是( )
A.(2,1) B.(-2,1)
C.(-3,-5) D.(3,-5)
3.已知坐标平面内点A(m,n)在第四象限,那
么点B(n,m)在( )
A.第一象限 B.第二象限.
C.第三象限 D.第四象限
D
B
4.若 <0,那么a(x,y)在第___象限。
5.点P(a,b)在第四象限,则a__0,b__0.
6.设M(a,b)为平面直角坐标系中的点。
①当a>0,b<0,点M在第几象限?
②当ab<0,点M位于第几象限?
③当a为任意实数,且b<0时,点M位于何处?
(纵坐标为b<0,说明点M位于x轴下方,
可以是y轴负半轴,第三或四象限。)
7.若a<0,则点P(-a,2)应在第___象限。
8.若点M(a+b,ab)在第三象限,则点N(a,b)
在第___象限。
9.在平面直角坐标系内,在第二象限内有一点P,且P到x轴的距离为3,到y轴的距离是5,则P点坐标为____.
10.在平面直角坐标系内第二象限内有一点A,且A
到x轴的距离为3,到y轴的距离是到x轴距离的3
倍,则A点坐标为____.
11.点M位于x轴下方,距x轴3个单位长,且位于y轴
左侧,距y轴2个单位长,则M点的坐标是____.
12.在平面直角坐标系中,点P的坐标为(-2,a?+1)
则点P所在象限是第____象限。
13.已知点P坐标为(2-a,3a+6)且点P到两坐
标轴的距离相等,则点P的坐标是( )
A.(3,3) B.(3,-3 )
C.(6,-6) D.(3,3)或(6,-6)
14.点A在x轴上,距离原点4个单位长度,
则A点的坐标是 ___________。
15.如果B(m+1,3m-5)到x轴的距离为它到y
轴距离相等,求m的值。
(4,0)或(-4,0)
第3课时
坐标特点
·
-2
-3
o
-1
1
·
·
·
·
·
·
-4
-1
4
(-4,3)
(4,3)
(-2,3)
(2,3)
(-2,-3)
(2,-3)
·
观察直角坐标系中下列各点.你能发现什么?
B
C
D
E
F
G
小结:
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
练习:
1.平行于横轴的直线上的点的_______相同;
平行于纵轴的直线上的点的_______相同;
2.已知平面直角坐标系内两点M(5,a),N(b,-2).
①若MN∥y轴,则a______,b____.
②若MN∥y轴,则a______,b____.
3.已知点M(3a-2,a+6),点N的坐标为(2,5)且直线MN∥x轴,求点M的坐标。
4.如果直线l∥x轴,且到x轴距离为5,那么直线l与
y轴交点的坐标是___.
5.已知点P1(a-1,5)和P2(2,b-1)到x轴距离相等,且P1P2∥y轴,则(a+b)2015的值为多少?
6.已知点M(3,a),N(b,-1),根据下列条件求a,b
的值。
①M、N两点关于x轴对称
②M、N两点的连线平行于y轴
③M、N两点在第二、四象限的角平分线上。
分别写出图中点A、B、C、D的坐标,
观察图形,并回答问题.
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点A与点B的位置有什么特点?
点A与点B的坐标有什么关系?
点A与点C的位置有什么特点?
点A与点C的坐标有什么关系?
关于x轴对称的点:横坐标相同,纵坐标互为相反数.
关于y轴对称的点:纵坐标相同,横坐标互为相反数.
A
B
C
D
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点B与点C的位置有什么特点?
点B与点C的坐标有什么关系?
关于原点对称的点:横坐标、纵坐标都互为相反数
A
B
C
D
归纳:
平面直角坐标系中的点p(x,y):
关于x轴的对称点是(x,-y);
关于y轴的对称点是(-x,y);
关于原点的对称点是p(-x,-y)。
关于x轴对称的点:横坐标相同,纵坐标互为相反数.
关于y轴对称的点:纵坐标相同,横坐标互为相反数.
关于原点对称的点:横坐标、纵坐标都互为相反数
练习:
1. 平面直角坐标系中的点p(x,y):
关于x轴的对称点是________;
关于y轴的对称点是________;
关于原点的对称点是_______。
2.点A(2,-3)关于x轴对称的点的坐标是____.
3.点B(-2,1)关于y轴对称的点的坐标是____.
4.点(4,3)与点(4,- 3)的关系是( ) . (A)关于原点对称 (B)关于 x轴对称 (C)关于 y轴对称 (D)不能构成对称关系
5.与点P(M,-1)关于原点的对称点是P(2,n),
则m+n的值为_______.
6.若点A(n,2)与B(-3,m)关于原点对称,
则n-m的值为______.
7.在平面直角坐标系中,点P(m?+1,-2)关于x轴对称的点在第___象限;关于y轴对称的点在第____象限。
观察图形,并回答问题.
点B和点C在第二、四象限的角平分线上,
(3,-3)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,3)
0
点B与点C的坐标有什么关系?
B
C
第二、四象限两坐标轴夹角平分线上的点;
的横、纵坐标互为相反数。
观察图形,并回答问题.
点A和点D在第二、四象限的角平分线上,
(2,2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-2,-2)
0
点A与点D的坐标有什么关系?
A
D
第一、三象限两坐标轴夹角平分线上的点
的横、纵坐标相等。
两坐标轴夹角平分线上的点的坐标的特征:
①第一、三象限两坐标轴夹角平分线上的点
的横、纵坐标相等。
②第二、四象限两坐标轴夹角平分线上的点
的横、纵坐标互为相反数。
练习:
1.第一、三象限两坐标轴夹角平分线上的点
的横、纵坐标______。
第二、四象限两坐标轴夹角平分线上的点
的横、纵坐标______。
2.已知点A(a,-2),B(-3,b)根据下列条件
求出a,b的值。
①A、B两点在二、四象限的角平分线上。
②A、B两点在一、三象限的角平分线上。
新题型 :利用坐标求线段长及图形面积
1.已知P(2,5),a(3,-4),则pa的长为( )
2.在直角坐标系中,画出以A(2,0)、B(-3,0)、
C(0,-3)为顶点的三角形,并求出△ABC的面积。
3.已知△ABC三顶点坐标为A(-2,0)、B(4,0)、
C(2,-3),求S△ABC
4.如图,已知A、B坐标分别为A(2,4)、B(4,1)
试求△ABO的面积。
C
你的收获!
