人教版七年级数学下册9.1.2不等式的性质课件(19张PPT)
文档属性
| 名称 | 人教版七年级数学下册9.1.2不等式的性质课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
复习回顾
等式的性质:
等式的基本性质1:在等式两边都加上(或减去)同一个数或式子,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以(或除以)同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0)
智力比拼
1:脑筋急转弯:小明家有两对父子,为什么只有三个人?
2:小明的爷爷a岁,爸爸b岁,请你用不等式表示他们年龄的大小关系?
3:两年后呢?三年前呢?
4:c年前呢?
发现规律
a>b
a+2>b + 2
a-3 > b - 3
a - c > b - c
猜想:不等式的两边加(或减)同一个数(或式子),不等号的方向不变
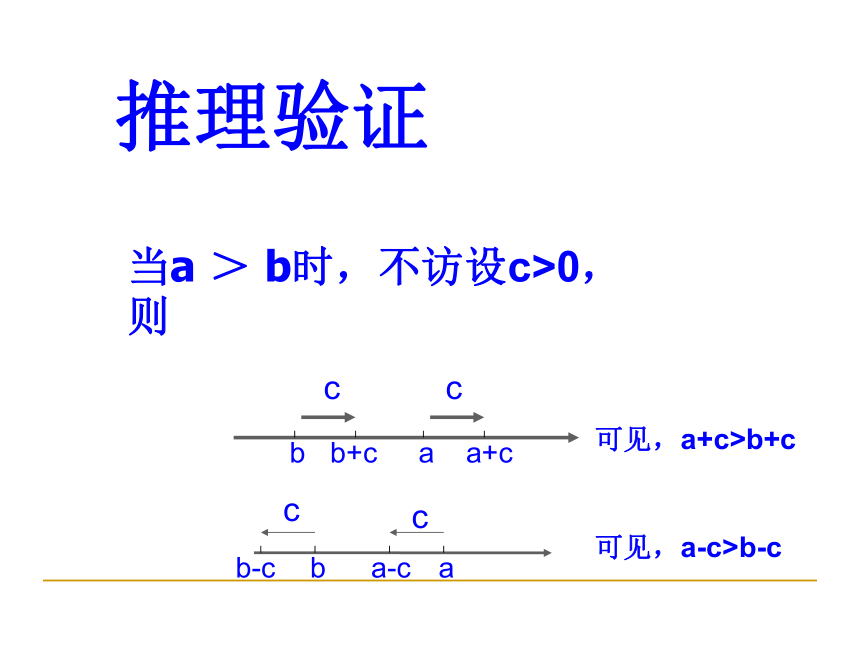
当a > b时,不访设c>0,则
a
b
b+c
a+c
c
c
可见,a+c>b+c
a
b
b-c
a-c
c
c
可见,a-c>b-c
推理验证
不等式的性质1
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b那么 a±c b±c
字母表示为:
﹥
等式的基本性质1:
在等式的两边都加(或减)同一个数(或式子),结果仍相等.
6÷5 ____ 2÷ 5 ,
6 ÷ (-5)____2÷ (-5)
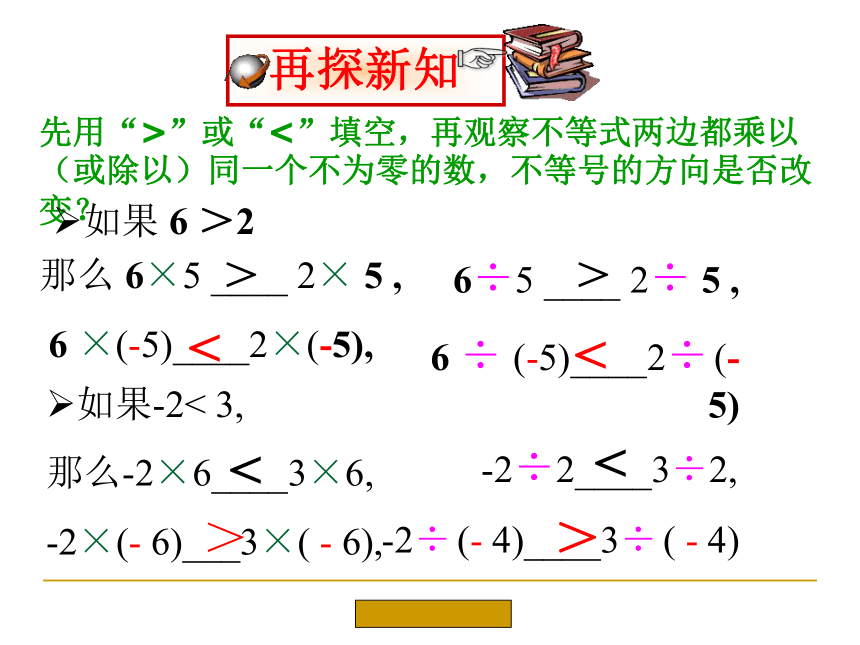
先用“>”或“<”填空,再观察不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
如果 6 >2
那么 6×5 ____ 2× 5 ,
6 ×(-5)____2×(-5),
>
如果-2< 3,
那么-2×6____3×6,
-2×(- 6)___3×( - 6),
-2÷2____3÷2,
-2÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
>
不等式的性质2 : 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0那么ac bc,
字母表示为:
>
>
不等式的性质 3 : 不等式的两边乘(或除以)同一个负数,不等号的方向改变
注:必须把不等号的方向改变
字母表示为:
如果a>b,c<0那么ac bc,
﹤
﹤
注:c能等于0吗?为什么?
争先恐后
用适当的不等号填空并说明根据
1.已知a>b,则a+1 b+1
2.已知a>b,则2a 2b
3.已知a>b,则-3a -3b
4.已知a>b,则-3a+2 -3b+2
判断,并说明理由:
1、如果a+c>b+c,那么a>b ( )
2、如果-4a>-4b,那么a>b ( )
3、如果2a+4>2b+4, 那么a>b ( )
4、如果2x>5x,两边同时除以x,
那么2>5 ( )
√
√
×
×
小试牛刀
例1:根据不等式的基本性质,把下列不等式化成
x<a或x>a的形式
(1)x-7>26
(2)3x<2x+1
(1)x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.为了使不等式x-7>26中不等号的一边变为x,
解:(1)根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
锋芒初试
(2) 3x<2x+1
解:根据不等式的性质1,不等式两边都减2x, 不等号的方向不变,得
3x-2x﹤2x+1-2x
x﹤1
这个不等式的解在数轴上的表示如图
言必有“据”
大显身手:
(3) —x﹥50
(4) -4x﹥3
3
2
勇攀高峰
有理数a 、b、 c在数轴上的对应点如图所示
用“>”号或“<”号填空
a + c___b + c
ab__cb
b÷a__c÷a
深入探究:
已知a ≠ 0 ,利用不等式的性质,比较3a与2a的大小。
课堂小结
本节课你学到了什么?
印象最深的是什么?
选作:习题9.1第8题。
复习回顾
等式的性质:
等式的基本性质1:在等式两边都加上(或减去)同一个数或式子,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2:在等式两边都乘以(或除以)同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc或 (c≠0)
智力比拼
1:脑筋急转弯:小明家有两对父子,为什么只有三个人?
2:小明的爷爷a岁,爸爸b岁,请你用不等式表示他们年龄的大小关系?
3:两年后呢?三年前呢?
4:c年前呢?
发现规律
a>b
a+2>b + 2
a-3 > b - 3
a - c > b - c
猜想:不等式的两边加(或减)同一个数(或式子),不等号的方向不变
当a > b时,不访设c>0,则
a
b
b+c
a+c
c
c
可见,a+c>b+c
a
b
b-c
a-c
c
c
可见,a-c>b-c
推理验证
不等式的性质1
不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b那么 a±c b±c
字母表示为:
﹥
等式的基本性质1:
在等式的两边都加(或减)同一个数(或式子),结果仍相等.
6÷5 ____ 2÷ 5 ,
6 ÷ (-5)____2÷ (-5)
先用“>”或“<”填空,再观察不等式两边都乘以(或除以)同一个不为零的数,不等号的方向是否改变?
如果 6 >2
那么 6×5 ____ 2× 5 ,
6 ×(-5)____2×(-5),
>
如果-2< 3,
那么-2×6____3×6,
-2×(- 6)___3×( - 6),
-2÷2____3÷2,
-2÷ (- 4)____3÷ ( - 4)
>
>
<
<
<
<
>
不等式的性质2 : 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a>b,c>0那么ac bc,
字母表示为:
>
>
不等式的性质 3 : 不等式的两边乘(或除以)同一个负数,不等号的方向改变
注:必须把不等号的方向改变
字母表示为:
如果a>b,c<0那么ac bc,
﹤
﹤
注:c能等于0吗?为什么?
争先恐后
用适当的不等号填空并说明根据
1.已知a>b,则a+1 b+1
2.已知a>b,则2a 2b
3.已知a>b,则-3a -3b
4.已知a>b,则-3a+2 -3b+2
判断,并说明理由:
1、如果a+c>b+c,那么a>b ( )
2、如果-4a>-4b,那么a>b ( )
3、如果2a+4>2b+4, 那么a>b ( )
4、如果2x>5x,两边同时除以x,
那么2>5 ( )
√
√
×
×
小试牛刀
例1:根据不等式的基本性质,把下列不等式化成
x<a或x>a的形式
(1)x-7>26
(2)3x<2x+1
(1)x-7>26
分析:解未知数为x的不等式,就是要使不等式逐步化为x﹥a或x﹤a的形式.为了使不等式x-7>26中不等号的一边变为x,
解:(1)根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
这个不等式的解集在数轴上的表示如图,
锋芒初试
(2) 3x<2x+1
解:根据不等式的性质1,不等式两边都减2x, 不等号的方向不变,得
3x-2x﹤2x+1-2x
x﹤1
这个不等式的解在数轴上的表示如图
言必有“据”
大显身手:
(3) —x﹥50
(4) -4x﹥3
3
2
勇攀高峰
有理数a 、b、 c在数轴上的对应点如图所示
用“>”号或“<”号填空
a + c___b + c
ab__cb
b÷a__c÷a
深入探究:
已知a ≠ 0 ,利用不等式的性质,比较3a与2a的大小。
课堂小结
本节课你学到了什么?
印象最深的是什么?
选作:习题9.1第8题。
