北师大版数学七年级下册4.3探究三角形全等的条件 同步练习(含答案)
文档属性
| 名称 | 北师大版数学七年级下册4.3探究三角形全等的条件 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 282.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-07 00:00:00 | ||
图片预览


文档简介
北师大版数学七年级下册4.3探究三角形全等的条件 同步练习
选择:
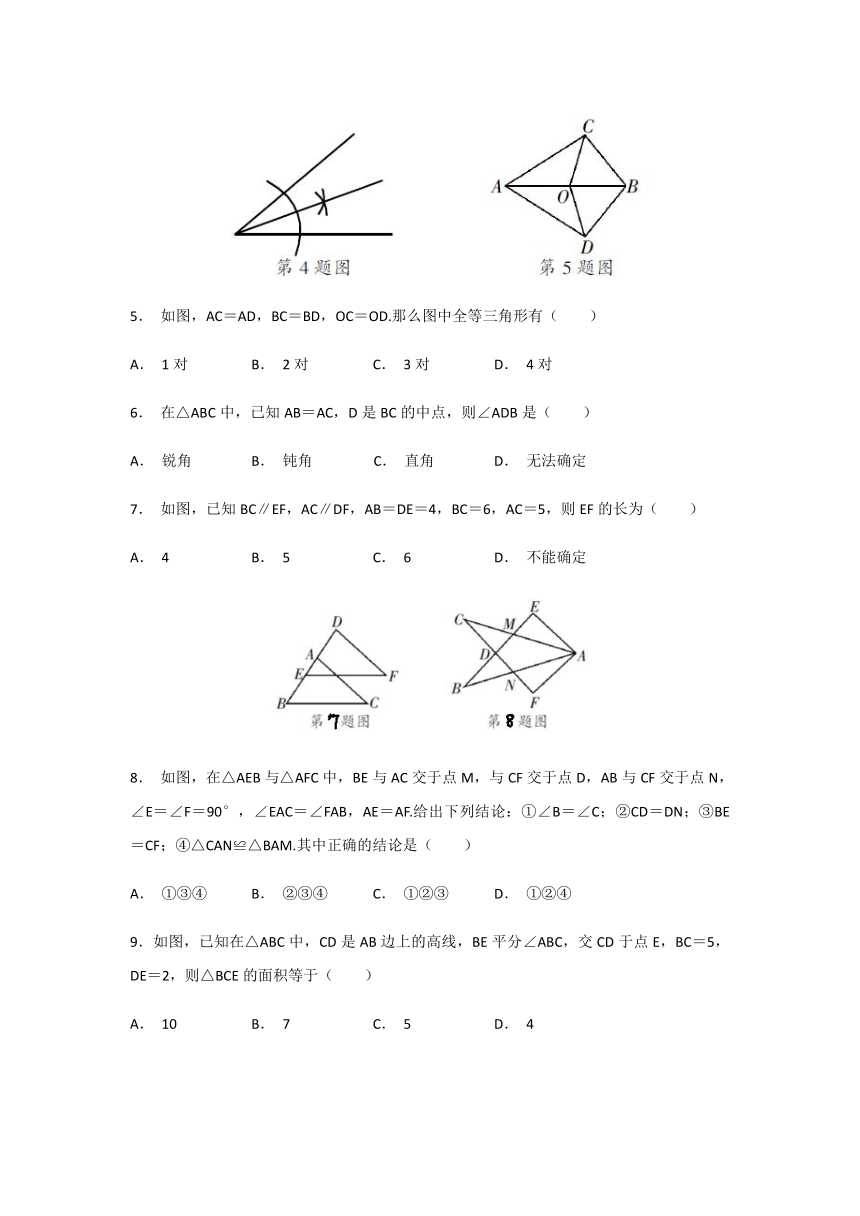
1. 如图,下列三角形中全等的是( )
A. ①② B. ②③ C. ③④ D. ①④
2.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠C等于( )
A. 15° B. 35° C. 50° D. 85°
3. (随州中考)如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A. 8 B. 9 C. 10 D. 11
4. 如图为作一个角的角平分线的示意图,该作法的依据是全等三角形判定的基本事实,可简写为( )
A. SSS B. SAS C. ASA D. AAS
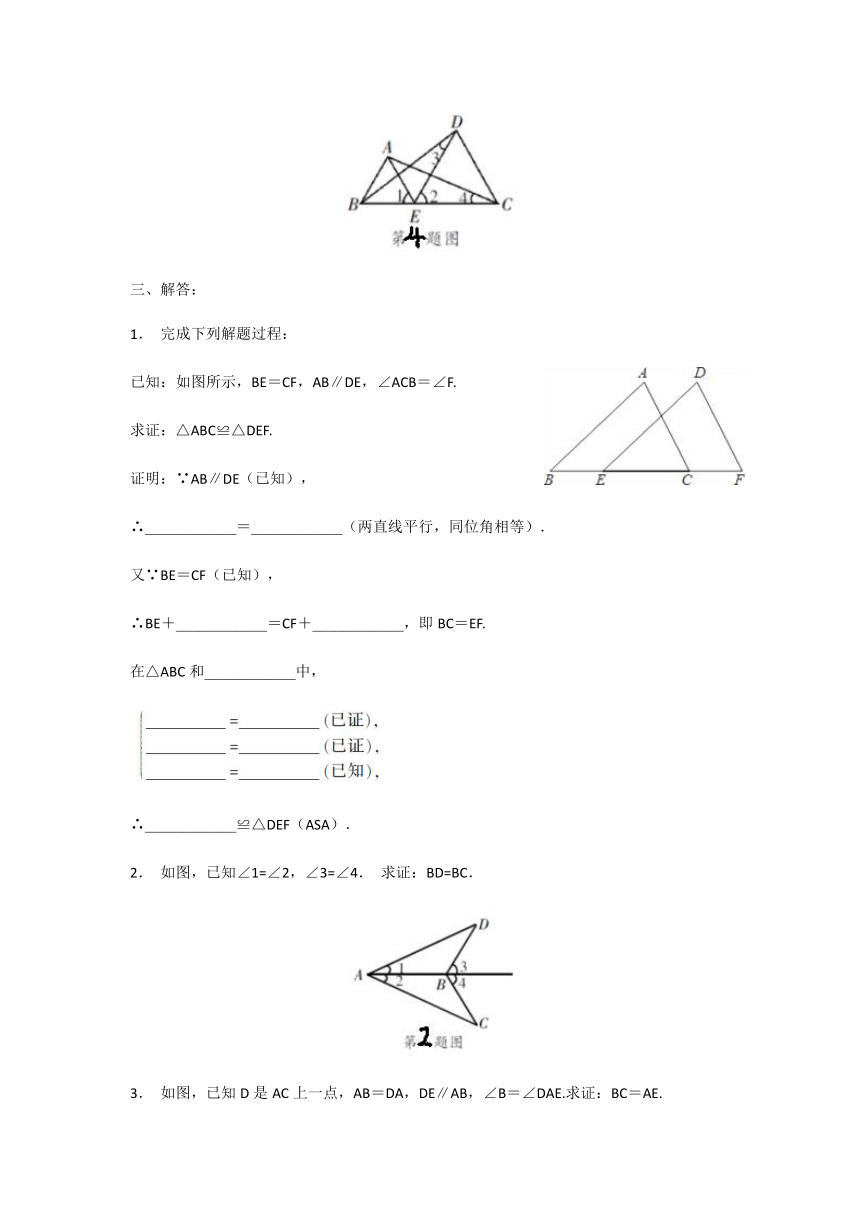
5. 如图,AC=AD,BC=BD,OC=OD.那么图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
6. 在△ABC中,已知AB=AC,D是BC的中点,则∠ADB是( )
A. 锐角 B. 钝角 C. 直角 D. 无法确定
7. 如图,已知BC∥EF,AC∥DF,AB=DE=4,BC=6,AC=5,则EF的长为( )
A. 4 B. 5 C. 6 D. 不能确定
8. 如图,在△AEB与△AFC中,BE与AC交于点M,与CF交于点D,AB与CF交于点N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△CAN≌△BAM.其中正确的结论是( )
A. ①③④ B. ②③④ C. ①②③ D. ①②④
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A. 10 B. 7 C. 5 D. 4
10.如图所示,已知∠1=∠2,AD=BC,AC,BD相交于点O,MN经过点O,则图中全等三角形的对数为( )
A. 4对 B. 5对 C. 6对 D. 7对
填空:
1. 如图,在△ABC中,E为边AB的中点,ED⊥AB,交BC于点D,且∠CAD=6°,∠B=48°,则∠BAC=____________.
2. 如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带____________去玻璃店.
3. 在△ABC和△DEF中,AB=4,∠A=35°,∠B=70°,ED=4,∠E=70°,则当∠D=____________时,可根据____________判断△ABC≌△DEF.
4. 如图,∠1=∠2,∠3=∠4,DE=CE,AE=4,则BE=____________.
解答:
1. 完成下列解题过程:
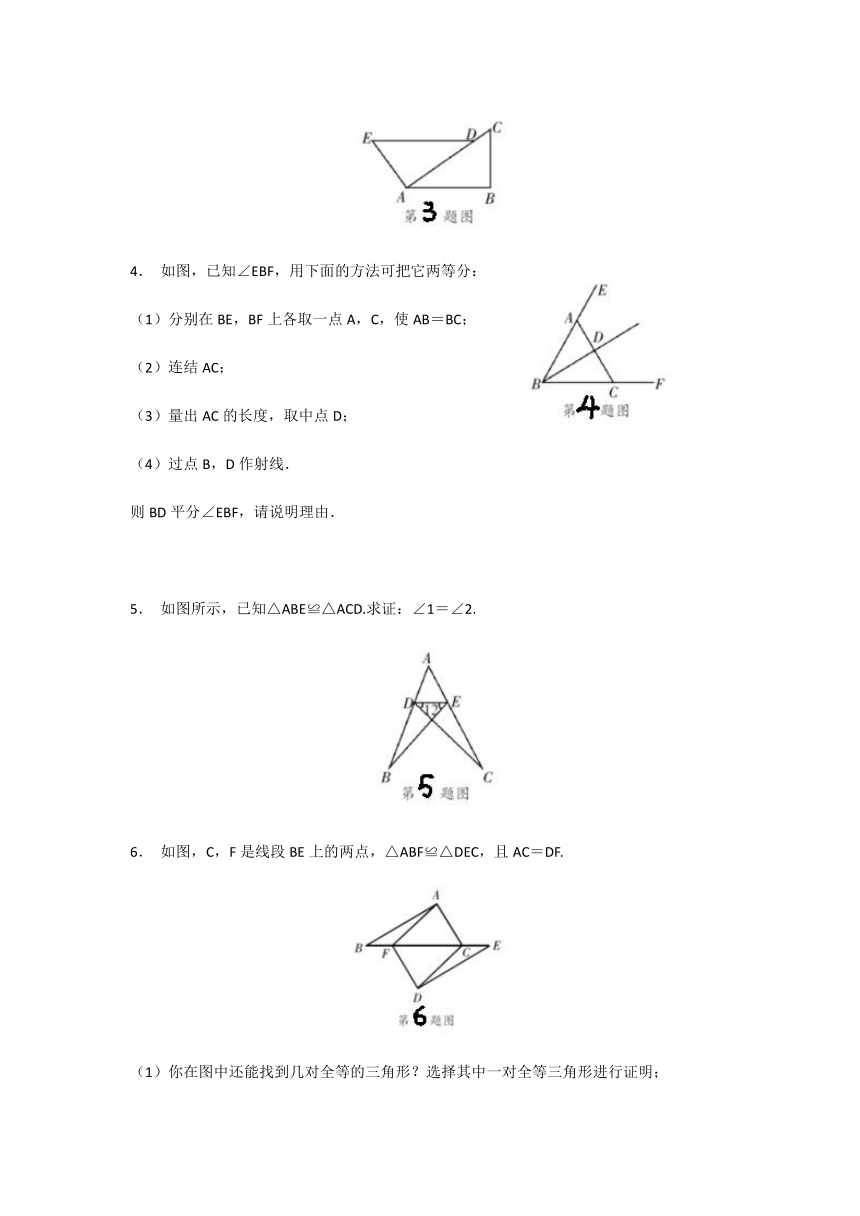
已知:如图所示,BE=CF,AB∥DE,∠ACB=∠F.
求证:△ABC≌△DEF.
证明:∵AB∥DE(已知),
∴____________=____________(两直线平行,同位角相等).
又∵BE=CF(已知),
∴BE+____________=CF+____________,即BC=EF.
在△ABC和____________中,
∴____________≌△DEF(ASA).
2. 如图,已知∠1=∠2,∠3=∠4. 求证:BD=BC.
3. 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.
4. 如图,已知∠EBF,用下面的方法可把它两等分:
(1)分别在BE,BF上各取一点A,C,使AB=BC;
(2)连结AC;
(3)量出AC的长度,取中点D;
(4)过点B,D作射线.
则BD平分∠EBF,请说明理由.
5. 如图所示,已知△ABE≌△ACD.求证:∠1=∠2.
6. 如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
(1)你在图中还能找到几对全等的三角形?选择其中一对全等三角形进行证明;
(2)∠ACE=∠BFD吗?试说明你的理由.
7. (湛江中考)如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
8. 如图,点D在BC上,DE与AC相交于点F,若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
9. 如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E. 试猜想CE与BD的数量关系,并说明理由.
10. (邵阳中考)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
11. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2.试说明BD=CE成立的理由.
参考答案
一、选择:
1-5 ABCAC 6-10 CCACC
二、填空:
1. 54°
2. ③
3. 35° ASA
4. 4
三、解答:
1. ∠B ∠DEF EC EC △DEF ∠B ∠DEF BC EF ∠ACB ∠F △ABC
2. ∵∠ABD+∠3=180°,∠ABC+∠4=180°,且∠3=∠4,∴∠ABD=∠ABC. 在△ADB和△ACB中,∴△ADB≌△ACB(ASA),∴BD=BC.
3. ∵DE∥AB,∴∠EDA=∠DAB,在△BAC和△ADE中,∵∴△BAC≌△ADE(ASA),∴BC=AE.
4. AB=BC,AD=DC,DB=DB可证△ABD≌△CBD,则∠ABD=∠CBD,即BD平分∠EBF.
5. ∵△ABE≌△ACD,∴AE=AD,AB=AC,DC=BE,∴AB-AD=AC-AE,即BD=EC,∵在△BDE和△CED中,∴△BDE≌△CED,∴∠1=∠2.
6. (1)还能找到2对全等三角形,分别是△ACF≌△DFC,△ABC≌△DEF. 理由如下:∵△ABF≌△DEC,∴AB=DE,BF=EC,AF=DC(全等三角形的对应边相等),∴BF+FC=EC+FC,即BC=EF. 在△ACF和△DFC中,∵∴△ACF
≌△DFC(SSS). 在△ABC和△DEF中,
∵∴△ABC≌△DEF(SSS).
(2)∠ACE=∠BFD.理由如下:∵△ABC≌△DEF,∴∠ACB=∠DFE(全等三角形的对应角相等). ∵∠ACB+∠ACE=180°,∠DFE+∠BFD=180°,∴∠ACE=∠BFD(等角的补角相等).
7. ∵AB∥ED,AC∥FD,∴∠B=∠E,∠ACB=∠DFE,∵BF=CE,∴BF+CF=CE+CF,即BC=EF,在△ABC和△DEF中,∵∴△ABC≌△DEF(ASA),∴AC=DF.
8. ∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE,∵∠3+∠DFC+∠C=∠2+∠AFE+∠E,又∵∠3=∠2,∠DFC=∠AFE,∴∠C=∠E,在△ABC和△ADE中,∵∴△ABC
≌△ADE(ASA).
9. CE=BD. 理由如下:延长CE交BA的延长线于点F,如图.
∵BE平分∠ABC,∴∠1=∠2. ∵CE⊥BD,∴∠BEC=∠BEF=90°. 又∵BE=BE,∴△BEC≌△BEF(ASA). ∴CE=FE=CF. ∵∠1+∠4=∠3+∠5=90°,∠4=∠5,∴∠1=∠3. 又∵∠BAD=∠CAF=90°,AB=AC,∴△BAD≌△CAF(ASA). ∴BD=CF. ∴CE=CF=BD.
10. (1)△ABE≌△CDF,△AFD≌△CEB(答案不唯一);
(2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,
∴△ABE≌△CDF(AAS).
11. ∵CD⊥AB,BE⊥AC,∠1=∠2,∴DO=EO(角平分线性质),∠BDO=∠CEO=90°,在△BDO和△CEO中,∵∴△BDO≌△CEO(ASA),∴BD=CE.
选择:
1. 如图,下列三角形中全等的是( )
A. ①② B. ②③ C. ③④ D. ①④
2.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠C等于( )
A. 15° B. 35° C. 50° D. 85°
3. (随州中考)如图,△ABC中,AB=5,AC=6,BC=4,边AB的垂直平分线交AC于点D,则△BDC的周长是( )
A. 8 B. 9 C. 10 D. 11
4. 如图为作一个角的角平分线的示意图,该作法的依据是全等三角形判定的基本事实,可简写为( )
A. SSS B. SAS C. ASA D. AAS
5. 如图,AC=AD,BC=BD,OC=OD.那么图中全等三角形有( )
A. 1对 B. 2对 C. 3对 D. 4对
6. 在△ABC中,已知AB=AC,D是BC的中点,则∠ADB是( )
A. 锐角 B. 钝角 C. 直角 D. 无法确定
7. 如图,已知BC∥EF,AC∥DF,AB=DE=4,BC=6,AC=5,则EF的长为( )
A. 4 B. 5 C. 6 D. 不能确定
8. 如图,在△AEB与△AFC中,BE与AC交于点M,与CF交于点D,AB与CF交于点N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△CAN≌△BAM.其中正确的结论是( )
A. ①③④ B. ②③④ C. ①②③ D. ①②④
9.如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A. 10 B. 7 C. 5 D. 4
10.如图所示,已知∠1=∠2,AD=BC,AC,BD相交于点O,MN经过点O,则图中全等三角形的对数为( )
A. 4对 B. 5对 C. 6对 D. 7对
填空:
1. 如图,在△ABC中,E为边AB的中点,ED⊥AB,交BC于点D,且∠CAD=6°,∠B=48°,则∠BAC=____________.
2. 如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带____________去玻璃店.
3. 在△ABC和△DEF中,AB=4,∠A=35°,∠B=70°,ED=4,∠E=70°,则当∠D=____________时,可根据____________判断△ABC≌△DEF.
4. 如图,∠1=∠2,∠3=∠4,DE=CE,AE=4,则BE=____________.
解答:
1. 完成下列解题过程:
已知:如图所示,BE=CF,AB∥DE,∠ACB=∠F.
求证:△ABC≌△DEF.
证明:∵AB∥DE(已知),
∴____________=____________(两直线平行,同位角相等).
又∵BE=CF(已知),
∴BE+____________=CF+____________,即BC=EF.
在△ABC和____________中,
∴____________≌△DEF(ASA).
2. 如图,已知∠1=∠2,∠3=∠4. 求证:BD=BC.
3. 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE.求证:BC=AE.
4. 如图,已知∠EBF,用下面的方法可把它两等分:
(1)分别在BE,BF上各取一点A,C,使AB=BC;
(2)连结AC;
(3)量出AC的长度,取中点D;
(4)过点B,D作射线.
则BD平分∠EBF,请说明理由.
5. 如图所示,已知△ABE≌△ACD.求证:∠1=∠2.
6. 如图,C,F是线段BE上的两点,△ABF≌△DEC,且AC=DF.
(1)你在图中还能找到几对全等的三角形?选择其中一对全等三角形进行证明;
(2)∠ACE=∠BFD吗?试说明你的理由.
7. (湛江中考)如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD,求证:AC=DF.
8. 如图,点D在BC上,DE与AC相交于点F,若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
9. 如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E. 试猜想CE与BD的数量关系,并说明理由.
10. (邵阳中考)如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
11. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE与CD相交于点O,且∠1=∠2.试说明BD=CE成立的理由.
参考答案
一、选择:
1-5 ABCAC 6-10 CCACC
二、填空:
1. 54°
2. ③
3. 35° ASA
4. 4
三、解答:
1. ∠B ∠DEF EC EC △DEF ∠B ∠DEF BC EF ∠ACB ∠F △ABC
2. ∵∠ABD+∠3=180°,∠ABC+∠4=180°,且∠3=∠4,∴∠ABD=∠ABC. 在△ADB和△ACB中,∴△ADB≌△ACB(ASA),∴BD=BC.
3. ∵DE∥AB,∴∠EDA=∠DAB,在△BAC和△ADE中,∵∴△BAC≌△ADE(ASA),∴BC=AE.
4. AB=BC,AD=DC,DB=DB可证△ABD≌△CBD,则∠ABD=∠CBD,即BD平分∠EBF.
5. ∵△ABE≌△ACD,∴AE=AD,AB=AC,DC=BE,∴AB-AD=AC-AE,即BD=EC,∵在△BDE和△CED中,∴△BDE≌△CED,∴∠1=∠2.
6. (1)还能找到2对全等三角形,分别是△ACF≌△DFC,△ABC≌△DEF. 理由如下:∵△ABF≌△DEC,∴AB=DE,BF=EC,AF=DC(全等三角形的对应边相等),∴BF+FC=EC+FC,即BC=EF. 在△ACF和△DFC中,∵∴△ACF
≌△DFC(SSS). 在△ABC和△DEF中,
∵∴△ABC≌△DEF(SSS).
(2)∠ACE=∠BFD.理由如下:∵△ABC≌△DEF,∴∠ACB=∠DFE(全等三角形的对应角相等). ∵∠ACB+∠ACE=180°,∠DFE+∠BFD=180°,∴∠ACE=∠BFD(等角的补角相等).
7. ∵AB∥ED,AC∥FD,∴∠B=∠E,∠ACB=∠DFE,∵BF=CE,∴BF+CF=CE+CF,即BC=EF,在△ABC和△DEF中,∵∴△ABC≌△DEF(ASA),∴AC=DF.
8. ∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,即∠BAC=∠DAE,∵∠3+∠DFC+∠C=∠2+∠AFE+∠E,又∵∠3=∠2,∠DFC=∠AFE,∴∠C=∠E,在△ABC和△ADE中,∵∴△ABC
≌△ADE(ASA).
9. CE=BD. 理由如下:延长CE交BA的延长线于点F,如图.
∵BE平分∠ABC,∴∠1=∠2. ∵CE⊥BD,∴∠BEC=∠BEF=90°. 又∵BE=BE,∴△BEC≌△BEF(ASA). ∴CE=FE=CF. ∵∠1+∠4=∠3+∠5=90°,∠4=∠5,∴∠1=∠3. 又∵∠BAD=∠CAF=90°,AB=AC,∴△BAD≌△CAF(ASA). ∴BD=CF. ∴CE=CF=BD.
10. (1)△ABE≌△CDF,△AFD≌△CEB(答案不唯一);
(2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,
∴△ABE≌△CDF(AAS).
11. ∵CD⊥AB,BE⊥AC,∠1=∠2,∴DO=EO(角平分线性质),∠BDO=∠CEO=90°,在△BDO和△CEO中,∵∴△BDO≌△CEO(ASA),∴BD=CE.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
