人教版 八年级下册数学 19.1.1 函数课件(共17张PPT)
文档属性
| 名称 | 人教版 八年级下册数学 19.1.1 函数课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
19.1.1 函数
问题1 :行驶路程s(千米)与行驶时间t(小时)的关系式为:S=60t.请填写下表:
当 确定一个值时, 就随之确定一个值。
时间t
路程S
t(秒) 1 2 3 4
s(米)
60
120
240
180
思考:问题中有几个变量?变量之间有什么联系?
问题2 :每张电影票的售价为10元,设某场电影售出x张票,票房收入为y元.
1500
2050
3100
当_______确定一个值时,______就随之确定一个值。
售出x张票 150 205 310
收入为y元
票数x
收入y
思考:问题中有几个变量?变量之间有什么联系?
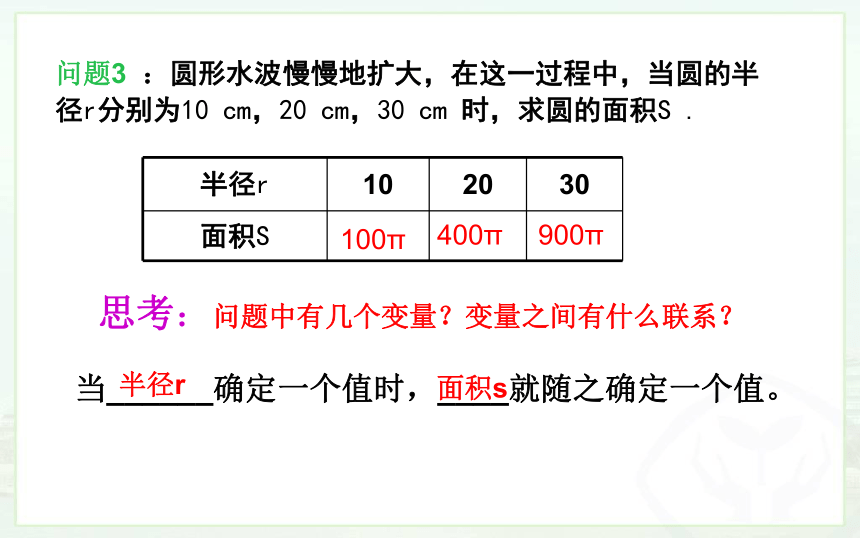
问题3 :圆形水波慢慢地扩大,在这一过程中,当圆的半径r分别为10 cm,20 cm,30 cm 时,求圆的面积S .
100π
400π
900π
当______确定一个值时,____就随之确定一个值。
半径r
面积s
半径r 10 20 30
面积S
思考:问题中有几个变量?变量之间有什么联系?
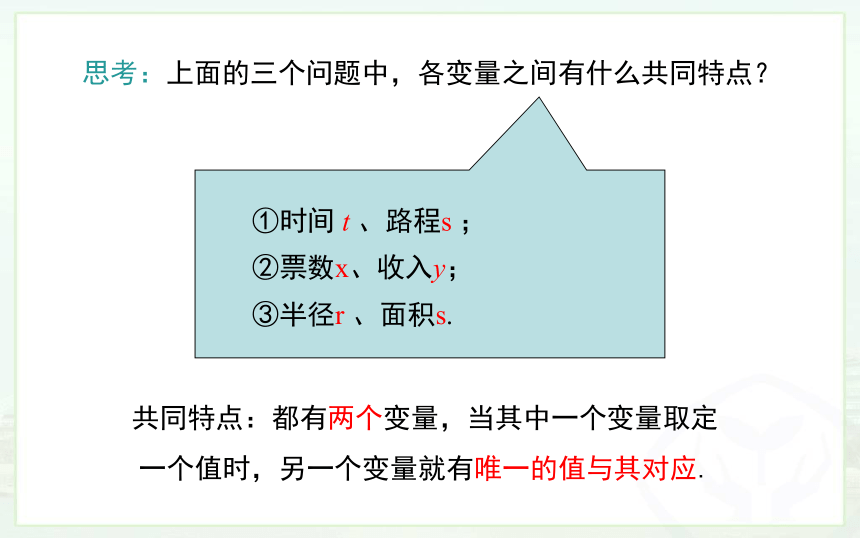
思考:上面的三个问题中,各变量之间有什么共同特点?
①时间 t 、路程s ;
②票数x、收入y;
③半径r 、面积s.
共同特点:都有两个变量,当其中一个变量取定一个值时,另一个变量就有唯一的值与其对应.
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
知识要点
函数满足:
必须有两个变量;
自变量x每确定一个值,y都有唯一确定的值与它对应.
典例精析
例1 下列关于变量x ,y 的关系式:
?y =2x+3;?y =x2+3;?y =|x|;④ ; ⑤y2-3x=10 .
其中表示y 是x 的函数关系的是 .
???
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量有唯一确定的值与它对应.
方法
一个x值有两个y 值与它对应
例2 下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积
B.正方形的边长与周长
C.等腰三角形的底边长与面积
D.圆的周长与半径
A中,长方形的宽一定.它是常量,而面积=长×宽,长与面积是两个变量,若长改变,则面积也改变,故A选项是函数关系;
B中,正方形的边长与周长是两个变量,若边长改变,则周长也改变,故B选项是函数关系;
C中,面积= ×底边上的高×底边长,底边长与面积虽然是两个变量,但面积公式中还有底边上的高,而这里高也是变量,有三个变量,故C选项不是函数关系;
D中,周长=2π×半径,圆的周长与其半径是函数关系.故选C.
C
解:(1)当x=2时,y= ;
当x=-3时,y=7.
例 已知函数
(1)求当x=2,-3时的函数值;
把自变量x的值带入关系式中,即可求出函数值.
(2)令
即当x= 时,y=0.
函数值:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
(2)求当x取什么值时,函数的值为0.
解得x=
例 汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
解:(1) 函数关系式为: y = 50-0.1x
叫做函数的解析式
(2)指出自变量x的取值范围;
解:由x≥0 及 50-0.1x ≥0
得 0 ≤ x ≤ 500
∴自变量的取值范围是0 ≤ x ≤ 500
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意各变量所代表的实际意义.
提示
汽车行驶里程,油箱中的油量均不能为负数!
例 汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
y = 50-0.1x
(3)汽车行驶200 km时,油箱中还有多少油?
(3)当 x = 200时,函数 y 的值为y=50-0.1×200=30.
因此,当汽车行驶200 km时,油箱中还有油30L.
(2)指出自变量x的取值范围;
0 ≤ x ≤ 500
例 汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
y = 50-0.1x
例1
写出等腰三角形中顶角的度数y与底角的度数x之间的函数解析式.
由题意得:2x+y=180°
顶角的度数y与底角的度数x之间的函数解析式为:y=180°-2x
写函数解析式的三个步骤:
根据题意找出相等关系;
根据相等关系写出含有两个变量的等式;
将等式变形,函数在左,自变量在右.
例2 下列函数中自变量x的取值范围是什么?
-2
x取全体实数
使函数解析式有意义的自变量的全体.
整式型
分式型
根式型
综合型
零次幂或
负整数指数幂型
x-1≠0,即x≠1
当堂练习
1.一个等腰三角形的周长为20,试写出它的底边y与腰长x之间的
函数关系式,并求出自变量x的取值范围.
解:由题意得 y与x的函数关系式为:y =20-2x
考虑边长为正数、三角形的三边关系:
x>0
20-2x>0
20-2x<2x
解得:20<x<40
当堂练习
2.有400本图书借给学生阅读,每人8本,求余下的书本数y与学生
人数x之间的函数解析式,并求出自变量x的取值范围.
解:由题意得 y与x的函数解析式为:y = 400 - 8x
因为y与x都是非负整数,所以
400 - 8x≥0
x ≥ 0
解得:0 ≤ x ≤ 50,且x为整数.
当堂练习
3.如图,等腰Rt△ABC的直角边长与正方形MNPQ的边长均为10cm,
AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右
运动,最后A点与N点重合.
(1)试写出重叠部分面积y(cm2)与MA长度x(cm)之间的函数解析式__________________.
(2)当MA=1cm时,重叠部分的面积是______.
y= x2 ,(0<x≤10)
cm2
19.1.1 函数
问题1 :行驶路程s(千米)与行驶时间t(小时)的关系式为:S=60t.请填写下表:
当 确定一个值时, 就随之确定一个值。
时间t
路程S
t(秒) 1 2 3 4
s(米)
60
120
240
180
思考:问题中有几个变量?变量之间有什么联系?
问题2 :每张电影票的售价为10元,设某场电影售出x张票,票房收入为y元.
1500
2050
3100
当_______确定一个值时,______就随之确定一个值。
售出x张票 150 205 310
收入为y元
票数x
收入y
思考:问题中有几个变量?变量之间有什么联系?
问题3 :圆形水波慢慢地扩大,在这一过程中,当圆的半径r分别为10 cm,20 cm,30 cm 时,求圆的面积S .
100π
400π
900π
当______确定一个值时,____就随之确定一个值。
半径r
面积s
半径r 10 20 30
面积S
思考:问题中有几个变量?变量之间有什么联系?
思考:上面的三个问题中,各变量之间有什么共同特点?
①时间 t 、路程s ;
②票数x、收入y;
③半径r 、面积s.
共同特点:都有两个变量,当其中一个变量取定一个值时,另一个变量就有唯一的值与其对应.
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
知识要点
函数满足:
必须有两个变量;
自变量x每确定一个值,y都有唯一确定的值与它对应.
典例精析
例1 下列关于变量x ,y 的关系式:
?y =2x+3;?y =x2+3;?y =|x|;④ ; ⑤y2-3x=10 .
其中表示y 是x 的函数关系的是 .
???
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量有唯一确定的值与它对应.
方法
一个x值有两个y 值与它对应
例2 下列变量间的关系不是函数关系的是( )
A.长方形的宽一定,其长与面积
B.正方形的边长与周长
C.等腰三角形的底边长与面积
D.圆的周长与半径
A中,长方形的宽一定.它是常量,而面积=长×宽,长与面积是两个变量,若长改变,则面积也改变,故A选项是函数关系;
B中,正方形的边长与周长是两个变量,若边长改变,则周长也改变,故B选项是函数关系;
C中,面积= ×底边上的高×底边长,底边长与面积虽然是两个变量,但面积公式中还有底边上的高,而这里高也是变量,有三个变量,故C选项不是函数关系;
D中,周长=2π×半径,圆的周长与其半径是函数关系.故选C.
C
解:(1)当x=2时,y= ;
当x=-3时,y=7.
例 已知函数
(1)求当x=2,-3时的函数值;
把自变量x的值带入关系式中,即可求出函数值.
(2)令
即当x= 时,y=0.
函数值:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
(2)求当x取什么值时,函数的值为0.
解得x=
例 汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
解:(1) 函数关系式为: y = 50-0.1x
叫做函数的解析式
(2)指出自变量x的取值范围;
解:由x≥0 及 50-0.1x ≥0
得 0 ≤ x ≤ 500
∴自变量的取值范围是0 ≤ x ≤ 500
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意各变量所代表的实际意义.
提示
汽车行驶里程,油箱中的油量均不能为负数!
例 汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
y = 50-0.1x
(3)汽车行驶200 km时,油箱中还有多少油?
(3)当 x = 200时,函数 y 的值为y=50-0.1×200=30.
因此,当汽车行驶200 km时,油箱中还有油30L.
(2)指出自变量x的取值范围;
0 ≤ x ≤ 500
例 汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
y = 50-0.1x
例1
写出等腰三角形中顶角的度数y与底角的度数x之间的函数解析式.
由题意得:2x+y=180°
顶角的度数y与底角的度数x之间的函数解析式为:y=180°-2x
写函数解析式的三个步骤:
根据题意找出相等关系;
根据相等关系写出含有两个变量的等式;
将等式变形,函数在左,自变量在右.
例2 下列函数中自变量x的取值范围是什么?
-2
x取全体实数
使函数解析式有意义的自变量的全体.
整式型
分式型
根式型
综合型
零次幂或
负整数指数幂型
x-1≠0,即x≠1
当堂练习
1.一个等腰三角形的周长为20,试写出它的底边y与腰长x之间的
函数关系式,并求出自变量x的取值范围.
解:由题意得 y与x的函数关系式为:y =20-2x
考虑边长为正数、三角形的三边关系:
x>0
20-2x>0
20-2x<2x
解得:20<x<40
当堂练习
2.有400本图书借给学生阅读,每人8本,求余下的书本数y与学生
人数x之间的函数解析式,并求出自变量x的取值范围.
解:由题意得 y与x的函数解析式为:y = 400 - 8x
因为y与x都是非负整数,所以
400 - 8x≥0
x ≥ 0
解得:0 ≤ x ≤ 50,且x为整数.
当堂练习
3.如图,等腰Rt△ABC的直角边长与正方形MNPQ的边长均为10cm,
AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右
运动,最后A点与N点重合.
(1)试写出重叠部分面积y(cm2)与MA长度x(cm)之间的函数解析式__________________.
(2)当MA=1cm时,重叠部分的面积是______.
y= x2 ,(0<x≤10)
cm2
