沪教版数学高二下春季班:第三讲平面及空间中的直线 同步学案(教师版)
文档属性
| 名称 | 沪教版数学高二下春季班:第三讲平面及空间中的直线 同步学案(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪教版数学高二下春季班第三讲
课题 平面及空间中的直线 单元 第十四章 学科 数学 年级 十一
学习 目标 1.知道平面的含义,理解平面的基本性质,会用文字语言、图形语言、集合语方表述平面的基本性质; 2.掌握确定平面的方法,并能运用于确定长方体的简单截面; 3.掌握空间直线与直线、直线与平面、平面与平面的各种位置关系,并能用图形、符号和集合语言予以表示.
重点 1.平面的基本性质,平行线的传递性; 2.空间直线与直线、直线与平面、平面与平面的各种位置关系及其表示方法.
难点 空间直线与直线、直线与平面、平面与平面的各种位置关系及其表示方法.
教学安排
版块 时长
1 知识梳理 30
2 例题解析 60
3 巩固训练 20
4 师生总结 10
5 课后练习 30
1、平面表示方法
平面用平行四边形表示,常用表示方法:①一个大写字母,②一个小写希腊字母,③三个或者三个以上的字母.
2、平面的基本性质
公理1、如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内.
推理模式: 如图示:
应用:是判定直线是否在平面内的依据,也可用于验证一个面是否是平面.
公理1说明了平面与曲面的本质区别.通过直线的“直”来刻划平面的“平”,通过直线的“无限延伸”来描述平面的“无限延展性”,它既是判断直线在平面内,又是检验平面的方法.
公理2、如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线.
推理模式:且且唯一 如图示:
应用:①确定两相交平面的交线位置;②判定点在直线上
公理2揭示了两个平面相交的主要特征,是判定两平面相交的依据,提供了确定两个平面交线的方法.
公理3、经过不在同一条直线上的三点,有且只有一个平面.
推理模式:不共线存在唯一的平面,使得
应用:①确定平面;②证明两个平面重合
“有且只有一个”的含义分两部分理解,“有”说明图形存在,但不唯一,“只有一个”说明图形如果有顶多只有一个,但不保证符合条件的图形存在,“有且只有一个”既保证了图形的存在性,又保证了图形的唯一性.在数学语言的叙述中,“确定一个”,“可以作且只能作一个”与“有且只有一个”是同义词,因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证.
推论1、经过一条直线和直线外的一点有且只有一个平面.
推理模式:存在唯一的平面,使得,
推论2、经过两条相交直线有且只有一个平面.
推理模式:存在唯一的平面,使得
推论3、经过两条平行直线有且只有一个平面.
推理模式:存在唯一的平面,使得
公理4、平行于同一条直线的两条直线互相平行.
推理模式:,
3、空间两直线的位置关系
(1)相交——有且只有一个公共点;
(2)平行——在同一平面内,没有公共点;
(3)异面——不在任何一个平面内,没有公共点.
4、异面直线
(1)异面直线定义:不同在任何一个平面内的两条直线.
(2)异面直线画法:
(3)异面直线证法:反证法,即证明两直线既不平行也不相交.
(4)求异面直线所成的角
异面直线所成的角是指过空间任意一点O分别作两条异面直线的平行线,所得的两条相交直线所成的锐角(或直角)。它的取值范围为.
辨析:异面直线所成的角的取值范围是;向量所成的角的取值范围是.
所以,用向量方法求异面直线所成的角时,如果得出的是钝角,还要修正为锐角.
异面直线所成的角求法:
① 几何法:通过直线搬动,具体搬动一条直线还是两条都搬动,要看实际情况;
② 代数法:采用向量运算.
1、平面及其基本性质
【例1】判断下列命题的真假,真的打“√”,假的打“×”
(1)可画一个平面,使它的长为,宽为; ( )
(2)一个平面的面积为; ( )
(3)光滑的桌面就是一个平面; ( )
(4)一条直线把它所在的平面分成两部分,一个平面把空间分成两部分; ( )
(5)若一条直线和一个平面仅有一个公共点,则称该平面经过这条直线; ( )
(6)若一条直线上有两个点在一个平面内,则称该平面经过这条直线; ( )
(7)经过面内任意两点的直线,若直线上各点都在这个面内,那么这个面是平面; ( )
(8)空间两个平面可将空间分成四部分. ( )
【难度】★
【答案】1.╳ 2.╳ 3.╳ 4.√ 5.╳ 6.√ 7.√ 8.╳
【例2】看图填空:
(1)点 平面;
(2)直线___________;
(3)直线 平面= ;
(4)直线 平面;
(5)直线___________.
(6)平面平面___________;
(7)平面平面___________;
(8)平面平面平面___________.
【难度】★
【答案】;;,;//;;;;
【例3】下列命题中,正确命题的序号是 .
(1)四边相等四边形为菱形;
(2)若四边形有两个对角都为直角,则这个四边形是圆内接四边形;
(3)“平面不经过直线”的等价说法是“直线上至多有一个点在平面内”;
(4)若两个平面有一条公共直线,则这两平面的所有公共点都在这条公共直线上.
【难度】★★
【答案】(3)(4)
【例4】下列命题正确的个数是 ( )
若共面,共面,则共面;
若共面,共面,则共面;
若共面,共面,共面,则共面;
若不共面,不共面,则不共面.
A.0 B.1 C.2 D.3
【难度】★★
【答案】A
【例5】下列说法正确的为 ( )
A.平面和只有一个公共点 B.两两相交的三条直线共面
C.不共面的四点中,任何三点不共线 D.有三个公共点的两平面必重合
【难度】★★
【答案】C
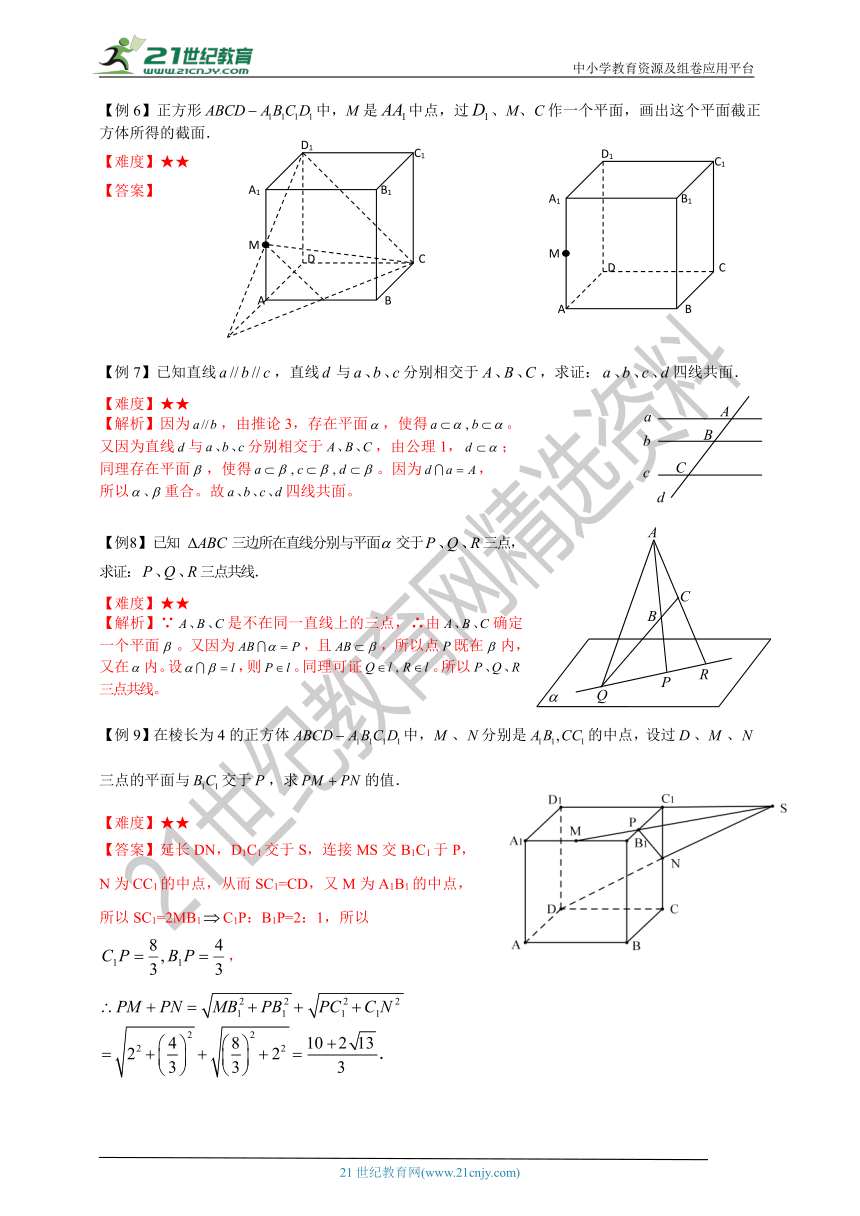
【例6】正方形中,M是中点,过、M、C作一个平面,画出这个平面截正方体所得的截面.
【难度】★★
【答案】
【例7】已知直线,直线与分别相交于,求证:四线共面.
【难度】★★
【解析】因为,由推论3,存在平面,使得。
又因为直线与分别相交于,由公理1,;
同理存在平面,使得。因为,
所以重合。故四线共面。
【例8】已知 三边所在直线分别与平面交于三点,求证:三点共线.
【难度】★★
【解析】∵是不在同一直线上的三点,∴由确定一个平面。又因为,且,所以点既在内,又在内。设,则。同理可证。所以三点共线。
【例9】在棱长为4的正方体中,、分别是的中点,设过、、三点的平面与交于,求的值.
【难度】★★
【答案】延长DN,D1C1交于S,连接MS交B1C1于P,
N为CC1的中点,从而SC1=CD,又M为A1B1的中点,
所以SC1=2MB1C1P:B1P=2:1,所以,
【例10】四面体ABCD中,E、G分别为BC、AB的中点,F在CD上,H在AD上,且有DF∶FC=2∶3,DH∶HA=2∶3.求证:EF、GH、BD交于一点.
【难度】★★
【解析】连结GE、HF,
∵E、G分别为BC、AB的中点,∴GE∥AC.
又∵DF∶FC=2∶3,DH∶HA=2∶3,∴HF∥AC.∴GE∥HF.
故G、E、F、H四点共面.
又∵EF与GH不能平行,∴EF与GH相交,设交点为O.
则O∈面ABD,O∈面BCD,而平面ABD∩平面BCD=BD.∴EF、GH、BD交于一点.
【巩固训练】
1.已知点,直线和平面.下列正确运用集合符号表示的是 .
(1); (2); (3);
(4); (5)若,则; (6)直线平面.
【难度】★
【答案】(2)(3)(5)(6)
直线与平面 _____ 时,称直线与平面相交于点,记作: _________ .
直线与平面 时,称直线平行于平面,记作: 或__________.
【难度】★
【答案】只有一个公共点,;没有公共点,,
3.在空间中,下列命题正确的是 ( )
A.对边相等的四边形一定是平面图形 B.四边相等的四边形一定是平面图形
C.有一组对边平行且相等的四边形是平面图形 D.有一组对角相等的四边形是平面图形
【难度】★★
【答案】C
4.下面是一些命题的叙述语(表示点,表示直线,表示平面)。其中命题和叙述方法都正确的是 ( )
A.∵,∴ B.∵,∴
C.∵,∴ D.∵,∴
【难度】★★
【答案】C
5.三个互不重合的平面把空间分成6个部分时,它们的交线有 条.
【难度】★★
【答案】1或2
6.给出下列四个命题:
①空间四点共面,则其中必有三点共线 ②空间四点不共面,则其中任何三点不共线
③空间四点中存在三点共线,则此四点共面 ④空间四点中任何三点不共线,则此四点不共面
其中正确的有( )
A.②和③ B.①②③ C.①和② D.②③④
【难度】★★
【答案】A
7.正方体中,对角线与平面交于点O,交于点M,求证:点共线.
【难度】★★
【解析】∵与截面交于点,、交于点
∴OM为平面与平面的交线
∵
∴在OM上,即三点共线.
2、空间中的直线
【例11】判断下列命题是否正确:
(1)若直线,则直线共面; ( )
(2)经过直线的平面有无数个; ( )
(3)梯形的对角线一定共面; ( )
(4)空间四边形的对角线所在直线异面; ( )
(5)在空间一个角的两边与另一个角的两边分别平行,则这两个角相等; ( )
(6)分别在两个平面内的两条直线异面; ( )
(7)在空间一个角的两边与另一个角的两边分别垂直相交,则这两个角相等. ( )
【难度】★
【答案】1.╳ 2.√ 3.√ 4.√ 5.╳ 6.╳ 7.╳
【例12】以下四个结论:
(1)若,则为异面直线;
(2)若,不真包含于,则为异面直线;
(3)没有公共点的两条直线是平行直线;
(4)两条不平行的直线就一定相交.
其中正确答案的个数为 ( )
A.0个 B.1个 C.2个 D.3个
【难度】★
【答案】C
【例13】已知直线和平面,,,,在内的射影分别为直线和,则的位置关系是( )
A.相交与平行 B.相交或异面
C.平行或异面 D.相交、平行或异面
【难度】★★
【答案】D
【例14】下列各图中,是正方体的顶点,是所在棱的中点,则直线与异面的图形的序号是 .
(1) (2) (3) (4)
【难度】★★
【答案】(2)(3)
【例15】一个正方体纸盒展开后如图所示,在原正方体纸盒中有下列结论:(1);(2)与成;(3)与是异面直线;(4),其中正确的是( )
A.(1)(2) B.(3)(4)
C.(2)(3) D.(1)(3)
【难度】★★
【答案】D
【例16】对于四面体ABCD,下列命题正确的是 .
(1)相对棱、AB与CD所在的直线异面;
(2)由顶点A作四面体的高,其垂足是的三条高线上的交点;
(3)若分别作和的边AB上的高,则这两条高所在的直线异面;
(4)分别作三组相对棱中点的连线,所得的三条线段相交于一点;
(5)最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
【难度】★★
【答案】(1)(4)(5)
【例17】已知平面平面,,,,且.
用反证法证明:是异面直线.
【难度】★★
【答案】假设b与c共面, ,b∩a=A ,,设b∩c=B,
又而c不在内,不可能有两个交点,与已知矛盾,所以是异面直线
【例18】如图所示,正方体ABCD - A1B1C1D1中,点M、N分别是直线A1B1、B1C1中点,问:
(1)AM和CN是否为异面直线?说明理由;
(2)D1B和C1C是否是异面直线?说明理由.
【难度】★★
【答案】(1)不是异面直线.
∵ 点M、N分别是直线A1B1、B1C1中点,∴MN∥A1C1.
∵A1A∥C1C,且 A1A = C1C,所以A1ACC1为平行四边形,∴A1C1= AC.
因为MN∥AC,所以A、M、N、C在同一平面内,
∴直线AM和CN共面.。
(2)是异面直线,下面用反证法证明:
假设D1B和C1C在同一平面D1CC1内,
则B∈平面D1CC1,C∈平面D1CC1,
推得BC平面D1CC1,与BC是正方体的棱矛盾.
∴假设不成立,D1B和C1C是异面直线.
【例19】在正方体中,分别是棱的中点.求:
(1)异面直线与所成的角;
(2)异面直线与所成的角.
【难度】★★
【答案】(1);(2).
【例20】已知四面体中,两两互相垂直,且,是中点,异面直线与所成的角大小为,求的长.
【难度】★★
【答案】4
【解析】过引的平行线,交的延长线于,连结,则是异面直线与所成的角。
∴。∵是的中点,∴是的中点,。
设,则,又,所以。
中,由余弦定理,,即的长为4。
【例21】是正三角形所在平面外一点,且∠=∠=∠=,、分别是、的中点,求异面直线SM与所成的角.
【难度】★★★
【答案】取CM中点P,则NP//SM,
从而∠PNB为SM与BN所成的角.
设SA=SB=SC=a,则AB=BC=AC=a,所以
又
所以.
∴异面直线与所成的角是.
【例22】长方体ABCD—A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:
(1)下列异面直线之间的距离:AB与CC1;AB与A1C1;AB与B1C;
(2)异面直线D1B与AC所成角的余弦值.
【难度】★★★
【答案】(1);(2)
【解析】(1)BC为异面直线AB与CC1的公垂线段,故AB与CC1的距离为b.
AA1为异面直线AB与A1C1的公垂线段,故AB与A1C1的距离为c.
过B作BE⊥B1C,垂足为E,则BE为异面直线AB与B1C的公垂线,BE==,即AB与B1C的距离为.
(2)解法一:连结BD交AC于点O,取DD1的中点F,连结OF、AF,则OF∥D1B,∴∠AOF就是异面直线D1B与AC所成的角.
∵AO=,OF= BD1=,AF=,
∴在△AOF中,cos∠AOF==.
解法二:如下图,在原长方体的右侧补上一个同样的长方体,连结BG、D1G,则AC∥BG,∴∠D1BG(或其补角)为D1B与AC所成的角.
BD1=,BG=,D1G=,
在△D1BG中,cos∠D1BG=
=-,故所求的余弦值为.
【例23】在空间四边形ABCD中,AD=AC=BD=BC=a,AB=CD=b,E、F分别是AB、CD的中点.
⑴求证:EF是AB和CD的公垂线;
⑵求AB和CD间的距离.
【难度】★★
【答案】
【例24】长方体中,分别是和的中点,求:(1)与所成的角;(2)与之间的距离;(3)与所成的角.
【难度】★★★
【答案】(1);(2);(3).
【巩固训练】
1.判断下列命题是否正确:
(1)若直线,与异面,则直线与异面; ( )
(2)若平面,直线,则与异面; ( )
(3)若直线,直线,且,则与异面; ( )
(4)若直线,则; ( )
(5)若,且,则. ( )
【难度】★
【答案】1.╳ 2.╳ 3.√ 4.╳ 5.√
2.若直线上有两个点在平面外,则 ( )
A.直线上至少有一个点在平面内 B.直线上有无穷多个点在平面内
C.直线上所有点都在平面外 D.直线上至多有一个点在平面内
【难度】★★
【答案】D
3.设为空间四点,命题甲:点不共面;命题乙:直线和不相交,那么甲是乙的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既非充分也非必要条件
【难度】★★
【答案】A
4.下列四个正方体图形中,为正方体的两个顶点,分别为其所在棱的中点,能得出 平面的图形的序号是( )
A. ①、③ B. ①、④ C. ②、③ D. ②、④
【难度】★★
【答案】B
5.右图是一个正方体的展开图,将它还原为正方体后,直线与的位置关系是 .
【难度】★★
【答案】平行
6.设空间四边形,分别是的中点,若,,且四边形的面积为,则与所成角为 .
【难度】★★
【答案】60o
7.空间四边形中,四条边和两条对角线构成了 对异面直线
【难度】★
【答案】3
8.一条直线与两条平行线中的一条是异面直线,那么它与另一条直线的位置关系是___________
【难度】★
【答案】相交或异面
9.教室内有一直尺,无论如何放置,地面总有直线与直尺所在直线 ( )
A.平行 B.垂直 C.相交 D.异面
【难度】★
【答案】B
10.若是异面直线,则只需具备的条件是 ( )
A.,平面,与不平行
B.,平面,,与无公共点
C.直线,,与不相交
D.平面,是的一条斜线
【难度】★
【答案】C
11.正方体中,下列各组异面直线所成的角最小的一组是 ( )
A.与 B.与 C.与 D.与
【难度】★★
【答案】D
12.正方体中。
(1)异面直线与所成的角为: ;
(2)异面直线与所成的角为: ;
(3)异面直线和所成的角为: ______.
【难度】★★
【答案】;;
13.如图所示,已知:E、F、G、H分别是正方体ABCD - A1B1C1D1的棱AB、BC、CC1、C1D1的中点,证明:FE、HG、DC三线共点.
【难度】★★
【解析】连接C1B,由题意知HC1∥EB,且HC1=EB,
∴四边形HC1BE是平行四边形,
∴HE∥C1B。又C1G=GC,CF=BF,故2GF=C1B且GF∥C1B,∴GF∥HE,且GF≠HE,
∴HG与EF相交,设交点为K,则K∈HG,HG面D1C1CD.因为K∈EF,EF面ABCD,
∴K∈面ABCD. ∵面D1C1CD面ABCD=DC,∴K∈DC,
∴EF、HG、DC三线共点.
14.在正方体ABCD—A1B1C1D1中,MN分别为A1B1、BB1的中点,求AM、CN所成的角.
【难度】★★
【答案】
15.在正方体中,分别是棱的中点.
则下面直线的位置关系是:
(1)与: ;
(2)与: ;
(3)与: ;
(4)与: .
【难度】★
【答案】异面,平行,相交,异面
16.如图,分别为空间四边形的边上的点,且,分别为上的点,且,则四边形的形状一定为 .
【难度】★★
【答案】梯形
1.用集合符号表示以下各概念:
(1)点在直线上:________;点不在直线上: .
(2)点在平面内:______;点不在平面内:_____________;
(3)直线在平面内:_________。平面经过直线: .
【难度】★
【答案】,;,;,.
2.判断下列命题的真假,真的打“√”,假的打“×”
(1)空间三点可以确定一个平面; ( )
(2)两条直线可以确定一个平面; ( )
(3)两条相交直线可以确定一个平面; ( )
(4)一条直线和一个点可以确定一个平面; ( )
(5)三条平行直线可以确定三个平面; ( )
(6)两两相交的三条直线确定一个平面; ( )
(7)两个平面若有不同的三个公共点,则两个平面重合; ( )
(8)若四点不共面,那么每三个点一定不共线. ( )
【难度】★
【答案】1.╳ 2.╳ 3.√ 4.╳ 5.╳ 6.╳ 7.╳ 8.√
3.已知顺次为空间四边形中边的中点.
(1)求证:四边形是平行四边形;
(2)如果,那么四边形是什么四边形?
(3)如果,那么四边形是什么四边形?
(4)如果,且,那么四边形是什么四边形?
【难度】★★
【答案】(1)略;(2)菱形;(3)矩形;(4)正方形.
4.能够确定一个平面的条件是: ; ; ; .
【难度】★
【答案】不共线的三点,一条直线和线外一点,两条平行直线,两条相交直线.
5.⑴三条直线两两相交,则由这三条直线可以确定 个平面;
⑵三条互相平行的直线可以确定 个平面;
⑶三条直线相交,仅有两个交点时可以确定的平面个数是 ;
⑷空间四条直线,其中每两条都相交,最多可以确定平面的个数是__________.
【难度】★
【答案】,,,
6.空间有五个点,其中共面,且也共面,那么这五个点是否共面: .
【难度】★
【答案】不一定
7.⑴若直线既不平行也不相交,则直线的位置关系是 ________;
⑵直线确定一个平面,则的位置关系为 ________.
【难度】★
【答案】异面,相交或平行
8.是异面直线,直线分别与都相交,则的位置关系为 .
【难度】★
【答案】相交或异面
9.若直线与直线都相交成角,则的位置关系是______.
【难度】★
【答案】平行、相交或异面
10.将正方体表面正方形的对角线称为面对角线.若是两条异面的面对角线,则它们所成的角大小可能为__________.
【难度】★
【答案】
11.梯形中,,平面,平面,则直线与平面内的直线的位置关系只能是_________________.
【难度】★
【答案】平行或异面
12.在长方体中,,则异面直线与所成的角的余弦值为_________.
【难度】★
【答案】
13.已知a、b为不垂直的异面直线,α 是一个平面,则a、b在α 上的射影可能是:①两条平行直线;②两条互相垂直的直线;③同一条直线;④一条直线及其外一点,则在上面的结论中,正确结论的编号是 (写出所有正确结论的编号)
【难度】★★
【答案】①②④
14.在平面上,两条直线的位置关系有相交、平行、重合三种.已知是两个相交平面,空间两条直线在上的射影是直线,在上的射影是直线. 用与,与的位置关系,写出一个总能确定与是异面直线的充分条件: .
【难度】★★
【答案】一组相交,一组平行
15.给定下列三个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②垂直于同一直线的两条直线相互平行;③过空间一点,存在一个平面,使得异面直线都与垂直;其中真命题的个数是( )
(A) (B) (C) (D)
【难度】★★
【答案】A
16.已知,、、不在同一平面内,,求证:和是异面直线.
【难度】★★
【答案】反证法.
若AD与BC不是异面直线,从而确定一个平面,设A、B、C确定的平面为α.
又,确定一个平面β,又,所以A、B、C β,
所以α与β重合,即,同理,这与、、不在同一平面内矛盾.
所以,和是异面直线.
17.如图,在空间四边形ABCD中,AB=CD=8,M、N分别是对角线BD、AC的中点,异面直线AB、CD所成角大小是,求线段MN的长.
【难度】★★
【答案】取棱AD的中点,连结MP、NP,
则MP,PN,
若,则,
若,则,
∴.
18.已知条互相平行的直线分别与直线l相交于点,求证:与l共面.
【难度】★★
【答案】略
19.在四棱锥中,底面是一直角梯形,,,,,且底面,与底面成角.
⑴若,为垂足,求证:;
⑵求异面直线与所成角的余弦值.
【难度】★★★
【答案】(1)略;(2).
平面与空间中的直线
知识梳理
例题解析
D
B1
C1
A1
D1
O1
B
C
A
O
A
D
C
B
A1
D1
C1
B1
M
A
D
C
B
A1
D1
C1
B1
M
a
b
c
d
A
B
C
A
B
C
P
Q
R
A
B
C
D
O
M
A
B
N
M
B
M
N
A
N
B
M
A
N
M
A
B
A
a
b
c
B1
C1
C
B
D
A1
D1
A
E
F
A
B
C
D
E
B
A
N
M
B1
C1
C
B
D
A1
D1
A
B1
C1
C
B
D
A1
D1
A
E
F
A
B
C
D
M
N
Q
P
课后练习
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
