沪教版数学高二下春季班:第四讲空间中的直线与平面1 同步学案(教师版)
文档属性
| 名称 | 沪教版数学高二下春季班:第四讲空间中的直线与平面1 同步学案(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
沪教版数学高二下春季班第四讲
课题 空间中的直线与平面1 单元 第十四章 学科 数学 年级 十一
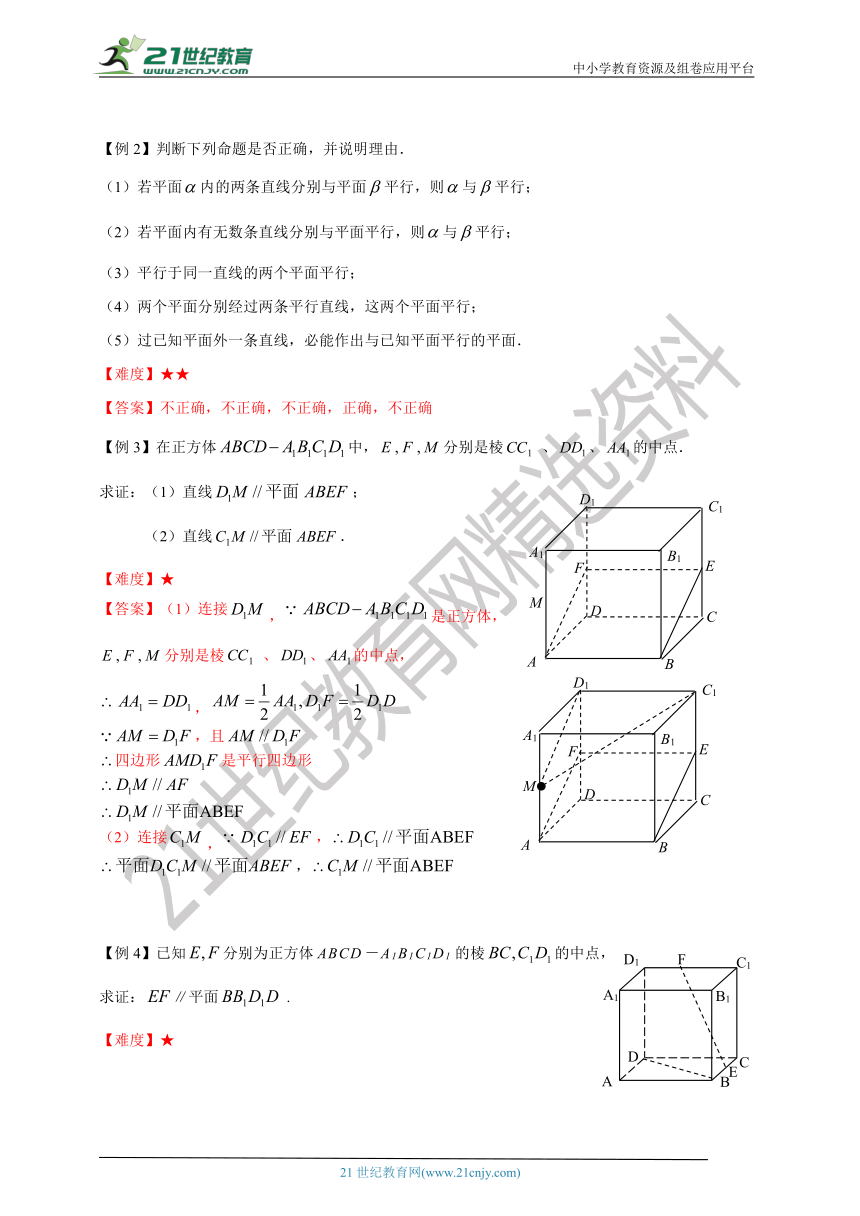
学习 目标 1.掌握直线与平面平行的定义、判定定理和性质定理,并能运用这些知识进行论证或解题; 2.掌握直线与平面垂直的定义、判定定理与性质定理,并能运用它们进行论证和解决有关问题
重点 1.理解掌握线线平行、线面平行之间的转化以及平行与垂直之间的转化的辩证关系; 2.证明垂直问题常常通过“线线垂直”与“线面垂直”之间的转化来实现,而证明“线线垂直”常常利用三垂线定理.
难点 证明垂直问题常常通过“线线垂直”与“线面垂直”之间的转化来实现,而证明“线线垂直”常常利用三垂线定理.
教学安排
版块 时长
1 知识梳理 30
2 例题解析 60
3 巩固训练 20
4 师生总结 10
5 课后练习 30
1、直线和平面的位置关系
(1)直线在平面内(无数个公共点);
(2)直线和平面相交(有且只有一个公共点);
(3)直线和平面平行(没有公共点)
2、线面平行
(1)判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.
(2)性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
3、线面垂直
(1)判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.
(2)性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.
1、直线与平面平行
【例1】判断真假:
(1)平行于同一直线的两直线平行( );
(2)平行于同一直线的两平面平行( );
(3)平行于同一平面的两直线平行( );
(4)平行于同一平面的两平面平行( );
(5)垂直于同一平面的两直线平行( );
(6)垂直于同一平面的两平面平行( );
(7)垂直于同一直线的两直线平行( );
(8)垂直于同一直线的两平面平行( );
(9)一个平面上不共线的三点到另一个平面距离相等,则这两个平面平行( );
(10)与同一条直线成等角的两个平面平行( ).
【难度】★★
【答案】1.√ 2.╳ 3.╳ 4.√ 5.√ 6.╳ 7.╳ 8.√ 9.╳ 10.╳
【例2】判断下列命题是否正确,并说明理由.
(1)若平面内的两条直线分别与平面平行,则与平行;
(2)若平面内有无数条直线分别与平面平行,则与平行;
(3)平行于同一直线的两个平面平行;
(4)两个平面分别经过两条平行直线,这两个平面平行;
(5)过已知平面外一条直线,必能作出与已知平面平行的平面.
【难度】★★
【答案】不正确,不正确,不正确,正确,不正确
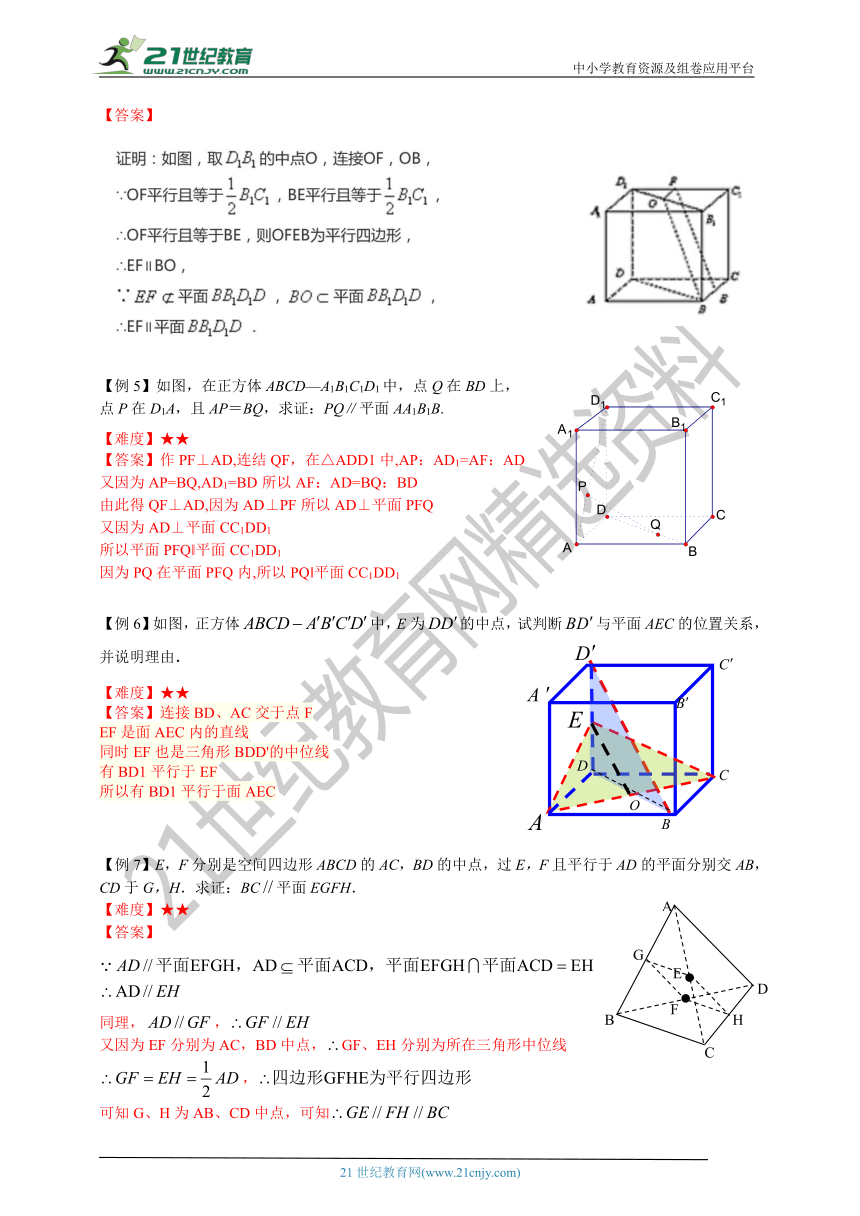
【例3】在正方体中,分别是棱、、的中点.
求证:(1)直线;
(2)直线.
【难度】★
【答案】(1)连接,是正方体,分别是棱、、的中点,
,
,且
四边形是平行四边形
(2)连接,,
,
【例4】已知分别为正方体ABCD-A1B1C1D1的棱的中点,
求证:∥平面.
【难度】★
【答案】
【例5】如图,在正方体ABCD—A1B1C1D1中,点Q在BD上,
点P在D1A,且AP=BQ,求证:PQ∥平面AA1B1B.
【难度】★★
【答案】作PF⊥AD,连结QF,在△ADD1中,AP:AD1=AF:AD
又因为AP=BQ,AD1=BD所以AF:AD=BQ:BD
由此得QF⊥AD,因为AD⊥PF所以AD⊥平面PFQ
又因为AD⊥平面CC1DD1
所以平面PFQ‖平面CC1DD1
因为PQ在平面PFQ内,所以PQ‖平面CC1DD1
【例6】如图,正方体中,E为的中点,试判断与平面AEC的位置关系,并说明理由.
【难度】★★
【答案】连接BD、AC交于点F
EF是面AEC内的直线
同时EF也是三角形BDD'的中位线
有BD1平行于EF
所以有BD1平行于面AEC
【例7】E,F分别是空间四边形ABCD的AC,BD的中点,过E,F且平行于AD的平面分别交AB,CD于G,H.求证:BC平面EGFH.
【难度】★★
【答案】
同理,,
又因为EF分别为AC,BD中点,GF、EH分别为所在三角形中位线
,
可知G、H为AB、CD中点,可知
【例8】ABCD是空间四边形,E、F、G、H分别是四边上的点,并且//面,//面,当是菱形时,____________________.
【难度】★
【答案】
【例9】已知异面直线、都平行于平面,且、在的两侧,若、与分别交于、两点,求证:;
【难度】★
【答案】连AD交于P,连MP、PN
∵CD∥,平面ACD∩=MP
∴CD∥MP
∴,同理可得,∴
【例10】如下图,设P为长方形ABCD所在平面外一点,M、N分别为AB、PD上的点,且=,求证:直线MN∥平面PBC.
【难度】★★
【答案】见解析
【解析】:要证直线MN∥平面PBC,只需证明MN∥平面PBC内的一条直线或MN所在的某个平面∥平面PBC.
证法一:过N作NR∥DC交PC于点R,连结RB,依题意得====NR=MB.∵NR∥DC∥AB,∴四边形MNRB是平行四边形.∴MN∥RB.又∵RB平面PBC,∴直线MN∥平面PBC.
证法二:过N作NR∥DC交PC于点R,连结RB,依题意有==,∴=,=+ + =.∴MN∥RB.又∵RB平面PBC,∴直线MN∥平面PBC.
【说明】 1:要证明直线与平面平行根据判定定理应该找平行线;但找平行线又根据性质定理的思想关键是找一个平面,借此可充分领会平行链的作用.
2.找平行线经常会用到平行线分线段成比例的性质.
3.鼓励学生一题多解,
【说明】本题重点考查直线与平面平行的性质.
【例11】两条异面直线、分别在平面、内,且=c,则直线 ( )
A.一定与,都相交 B.至少与,中的一条相交
C.至多与,中的一条相交 D.一定与,都不相交
【难度】★★
【答案】B
【例12】如图,在正方形ABCD外有一点S到A、B、C、D四点距离相等,底面ABCD的边长为,SA=SB=SC=SD=2,P、Q分别在BD和SC上,且BP : PD=1 : 2, PQ∥平面SAD,求线段PQ的长.
【难度】★★★
【答案】
【巩固训练】
1.如果平面外一条直线上有两个点到这个平面的距离相等,则这条直线与平面关系是________.
【难度】★
【答案】平行,相交
2.若直线平面,则直线与平面内的直线的位置关系是 .
【难度】★
【答案】平行、异面
3.用表示一个平面,l表示一条直线,则平面内至少有一条直线与l( )
A.平行 B.相交 C.异面 D.垂直
【难度】★
【答案】D
4.正方体中,点分别是正方形的中心.
(1)直线平面的位置关系是 ;
(2)直线与所成的角为 ;
(3)平面与平面的位置关系是 .
【难度】★
【答案】平行,,平行
5.直线与平面平行的充要条件是 ( )
A.直线与平面内的一条直线平行
B.直线与平面内的两条直线不相交
C.直线与平面内的无数条直线平行
D.直线与平面内的任意直线都不相交
【难度】★
【答案】D
6.如果直线和两个相交平面都平行,那么这条直线和这两个相交平面的交线的位置关系是( )
A.平行 B.相交 C.异面 D.以上情况都有可能
【难度】★
【答案】A
7.已知直线平面,则直线与平面的位置关系是__________。
【难度】★
【答案】或
8.若直线平面,则下列命题中正确的是 ( )
A.平行于内所有直线 B.平行于过的平面与的交线
C.平行于内的任一直线 D.平行于内唯一确定的直线
【难度】★★
【答案】B
9.已知直线和平面,那么的一个必要不充分条件是 ( )
A. B. C. D.与成等角
【难度】★★
【答案】D
10.表示两个平面,表示两条直线,则的一个充分条件是 ( )
A. B. C. D.
【难度】★★
【答案】D
11.两个全等的正方形ABCD和ABEF所在平面相交于AB,MAC,NFB且AM=FN,求证:MN∥平面BCE.
【难度】★★
【答案】平面MNH // 平面BCE,则平面MNH 上任一直线‖平面BCE,则得证
12.设a、b是异面直线,AB是a、b的公垂线,过AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与AB交于点P,求证:P是MN的中点.
【难度】★★
【答案】证明:连接AN,交平面α于点Q,连接PQ.
∵b∥α,b平面ABN,平面ABN∩α=OQ,
∴b∥OQ.又O为AB的中点,
∴Q为AN的中点.∵a∥α,a平面AMN且平面AMN∩α=PQ,
∴a∥PQ.∴P为MN的中点.
2、直线与平面垂直
【例13】判断正误:
(1)若直线垂直于平面内两条直线,则; ( )
(2)过一定点与已知平面垂直的直线有无数条; ( )
(3)过一定点与已知直线垂直的直线都在同一平面内; ( )
(4)若直线,,则; ( )
(5)若,直线,则; ( )
(6)若,,且,则线段的长度是直线与平面的距离.( )
【难度】★★
【答案】1.╳ 2.╳ 3.√ 4.√ 5.╳ 6.╳
【例14】已知RtABC中,,PA平面ABC,AEPC于E,求证:AE平面PBC.
【难度】★★
【答案】
【例15】 P是△ABC所在平面外的一点,P在平面ABC内的射影是O,①若PA=PB=PC,则O是△ABC的外心;②若P到△ABC的三边所在直线的距离相等,且O在△ABC内,则O是△ABC的内心;③若PA、PB、PC两两互相垂直,则O是△ABC的垂心;④若PA=PB=PC,且O在边AB上,则△ABC是直角三角形。正确的命题是 .
【难度】★★
【答案】①②③④
【例16】直角梯形ABCD中,,,,平面.求证:(1);(2).
【难度】★★
【答案】(1)(2)
【例17】如图,在四面体ABCD中,CD⊥BD,CD⊥AD,过△ABC内一点P画一直线与CD垂直,应如何画?说明理由.
【难度】★★
【答案】在AB边上任取一点M,连接CM,DM,使P在CM上,作PQ∥DM交CD于点Q,则PQ就是要画的直线.
证明:因为CD⊥BD,CD⊥AD,所以CD⊥平面ABD,所以CD垂直平面ABD内任何直线,所以CD⊥DM,在平面CDM中,PQ∥DM,所以PQ⊥CD.
【例18】在正方体中,与正方体的一条对角线垂直的各面的对角线的条数是 .
【难度】★★
【答案】6
【例19】正四棱柱中,,点在上且. 证明:平面;
【难度】★★
【答案】依题设知,.(Ⅰ)连结交于点,则.
由三垂线定理知,. 在平面内,连结交于点,
由于,故,,
与互余.于是.与平面内两条相交直线都垂直,
所以平面.
【例20】已知PD垂直于矩形ABCD所在的平面,M、N分别是AD、PB的中点(如图),求证:MN⊥AD.
【难度】★★
【答案】连接BD,过N点作PD的平行线NQ,Q点落在BD上且平分BD,三角形PDB的中位线NQ垂直于BD,也垂直于矩形ABCD,所以NQ垂直于AD,连接MQ,中位线MQ平行于AB且垂直于AD ,所以AD就垂直于三角形MNQ,就得到AD垂直于MN.
【例21】已知直线a⊥平面,直线b⊥平面,O、A为垂足.求证:a∥b.
【难度】★
【答案】略
【例22】已知PA⊥⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过A点作AE⊥PC于点E,求证:AE⊥平面PBC.
【难度】★★
【答案】证明:∵PA⊥平面ABC,∴PA⊥BC.
又∵AB是⊙O的直径,∴BC⊥AC.而PC∩AC=C,∴BC⊥平面PAC.
又∵AE在平面PAC内,∴BC⊥AE.
∵PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC
【例23】如图,AB为⊙O的直径,C为⊙O上一点,AD⊥平面ABC,AE⊥BD于E,AF⊥CD于F,求证:BD⊥平面AEF.
【难度】★★
【答案】因为AB是直径,所以BC⊥AC;又AD⊥面ABC,所以BC⊥AD,于是知BC⊥面ACD,可知BC⊥AF.又AF⊥CD,且AF⊥BC,所以AF⊥面BCD,即知AF⊥BD.又BD⊥AE,所以BD⊥平面AEF
【例24】正方形ABCD的边长是,为其中心.平面ABCD外一点P到正方形各顶点的距离都是,M、N分别是PA、BD上的点,且;
求证:(1)平面ABCD ;(2)平面.
【难度】★★
【答案】
(1)连接AC、BD,可知交点为O,连接PO,可知为等腰三角形,,同理,
(2)证明:连结AN并延长和BC交于E点,由PM:MA=BN:ND,可得EN:NA=BN:ND=MP:MA,即?
∴MN∥PE,而MN?平面PBC,PE?面PBC,∴MN∥平面PBC
【例25】如图1所示,为正方形,⊥平面,过且垂直于的平面分别交于.求证:,.
【难度】★★★
【答案】∵SA⊥平面ABCD,BC?平面ABCD,∴BC⊥SA,
∵四边形ABCD为正方形,∴BC⊥AB,
∵AB、SA是平面SAB内的相交直线,∴BC⊥平面SAB.
∵AE?平面SAB,∴BC⊥AE.
∵SC⊥平面AEFG,AE?平面AEFG,∴SC⊥AE,
∵BC、SC是平面SBC内的相交直线,∴AE⊥平面SBC.
∵SB?平面SBC,∴AE⊥SB.
同理可证AG⊥SD.
【例26】如图2,在三棱锥中,,,作,E为垂足,作于.求证:.
【难度】★★★
【答案】取AB中点F,连接CF,DF;
∵BC=AC,AD=BD,∴AB⊥CF,AB⊥DF,CF∩DF=F;
∴AB⊥平面CDF,CD?平面CD;
∴CD⊥AB,CD⊥BE,BE∩AB=B;
∴CD⊥平面ABE,AH?平面ABE;
∴CD⊥AH,即AH⊥CD,又AH⊥BE,BE∩CD=E;
∴AH⊥平面BCD.
【例27】如图:斜边为AB的与PB交于E,
求证:平面.
【难度】★★★
【答案】BC⊥PC,?BC⊥AC,?∴BC⊥PAC,?PBC⊥PAC,(BC∈PBC).又AF⊥PC(交线)
?∴AF⊥PBC,?AF⊥PB,又AE⊥PB,∴AEF⊥PB,EF⊥PB.∴PB⊥平面AEF
【例28】下列五个正方体图形中,是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出⊥面MNP的图形的序号是 .(写出所有符合要求的图形序号)
【难度】★★★
【答案】①④
【巩固训练】
13.“直线垂直于平面内的无数条直线”是“”的_______条件.
【难度】★
【答案】必要非充分
14.若直线与平面不垂直, 那么平面内与直线垂直的直线有_________条.
【难度】★
【答案】无数
15.直线与平面斜交,那么在内与垂直的直线 ( )
A.没有 B.有一条
C.有无数条 D.有条(为大于1的整数)
【难度】★
【答案】C
16.如果直线平面,直线,直线与的位置关系是 ( )
A. B. C.一定异面 D.一定相交
【难度】★
【答案】B
17.(1)如图7,在正方体ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,判断下列结论是否正确:
①AC⊥面CDD1C1 ②A A 1⊥面A1B1C1D1
③AC⊥面BDD1B1 ④ EF⊥面BDD1B1
⑤AC⊥BD1
(2)将(1)中正方体改成长方体呢,以上结论是否正确?
【难度】★★
【答案】②③④⑤,不正确
18.若平面,中,,则的形状是 .
【难度】★
【答案】直角三角形
19.直线垂直于平面内的两条直线,则直线与平面的关系是 ( )
A.垂直 B.平行 C.相交 D.都有可能
【难度】★
【答案】D
20.直线不垂直于平面,则内与垂直的直线共有 ( )
A.0条 B.1条 C.无数条 D.内所有直线
【难度】★
【答案】C
21.在正方体ABCD-A1B1C1D1中,E、F分别是AA1、CC1的中点,,连接,求证:.
【难度】★★
【答案】略
22.在正方体ABCD-A1B1C1D1中,为底面ABCD的中心,F为CC1的中点,求证:.
【难度】★★
【答案】证明:连接FO.
∵DB⊥A1A,DB⊥AC,A1A∩AC=A,∴DB⊥平面A1ACC1.
又A1O?平面A1ACC1,∴A1O⊥DB.
∵tan∠AA1O=,tan∠FOC=,∴∠AA1O=∠FOC,
则∠A1OA+∠FOC=90°.∴A1O⊥OF.
∵OF∩DB=O,∴A1O⊥平面FBD.
23.如图:正方体ABCD-ABCD中,S,T分别为棱上的点,
如果,那么是( )
A.锐角 B.直角 C.钝角 D.以上都有可能
【难度】★★
【答案】B
24.如图:P是ABC所在平面外的一点,且PA平面ABC.若O和Q分别是ABC和PBC的垂心.求证:OQ平面PBC.
【难度】★★★
【答案】证明:∵O是△ABC的垂心,∴BC⊥AE.∵PA⊥平面ABC,根据三垂线定理得BC⊥PE.
∴BC⊥平面PAE.∵Q是△PBC的垂心,故Q在PE上,则OQ?平面PAE,∴OQ⊥BC.
∵PA⊥平面ABC,BF?平面ABC,∴BF⊥PA,又∵O是△ABC的垂心,
∴BF⊥AC,故BF⊥平面PAC.因而FM是BM在平面PAC内的射影.
因为BM⊥PC,据三垂线定理的逆定理,FM⊥PC,
从而PC⊥平面BFM.又OQ?平面BFM,所以OQ⊥PC.
综上知OQ⊥BC,OQ⊥PC,
所以OQ⊥平面PBC
1.判断正误:
(1)若直线,,则;( )
(2)若直线,,且都在平面内,则;( )
(3)若直线,,则直线;( )
(4)若平面,直线,则直线;( )
(5)直线,平面,则直线;( )
(6)平面,平面,则直线;( )
(7)若平面直线,直线,且和没有公共点,则.( )
【难度】★
【答案】1.╳ 2.√ 3.╳ 4.╳ 5.╳ 6.√ 7.√
2.如果直线平面,①若直线,则;②若,则;③若,则;④若,则.上述判断正确的是: ( )
A.①②③ B.②③④ C.①③④ D.②④
【难度】★★
【答案】B
3.关于直线以及平面,下列说法正确的是 ( )
A.若,则
B.若,则
C.若,则
D.若,则
【难度】★★
【答案】D
4、如图,三棱柱中,侧棱,底面三角形是正三角形,是中点,则下列叙述正确的是( )
A.与是异面直线
B.平面
C.,为异面直线,且
D.平面
【难度】★★
【答案】C
5、如图,在正四棱锥中,分别是,,的中点,动点在线段上运动时,下列四个结论:①;②;③面;④面.中恒成立的为( )
①③ B.③④ C.①② D.②③④
【难度】★★
【答案】A
6、已知一条直线与一个平面内的两条直线垂直.则该直线与这个平面的位置关系为( )
A.平行 B.相交 C.在平面内 D.都有可能
【难度】★★
【答案】D
7、如图,直线平面,垂足为,已知边长为的等边三角形在空间做符合以下条件的自由运动:①,②,则两点间的最大距离为( )
B. C. D.
【难度】★★★
【答案】C
8、已知矩形,,,沿着对角线所在的直线进行翻折,在翻折过程中( )
A. 存在某个位置,使得直线与垂直;
B. 存在某个位置,使得直线与垂直;
C. 存在某个位置,使得直线与垂直;
D. 对任意位置,三直线“与”、“与”、“与”均不垂直.
【难度】★★★
【答案】B
9.点P是平行四边形ABCD所在平面外一点,O是对角线AC与BD的交点,且PA=PC,PB=PD. 求证:PO⊥平面ABCD.
【难度】★★
【答案】∵PA=PC,PB=PD,∴PO⊥AC,PO⊥BD
平面PAC交平面PBD于PO,所以PO⊥平面ABCD
10.如图,已知M、N、P、Q分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
求证:(1)线段MP和NQ相交且互相平分;(2)AC∥平面MNP,BD∥平面MNP.
【难度】★★
【解析】(1) ∵M、N是AB、BC的中点,∴MN∥AC,MN=AC.
∵P、Q是CD、DA的中点,∴PQ∥CA,PQ=CA.
∴MN∥QP,MN=QP,MNPQ是平行四边形.
∴□MNPQ的对角线MP、NQ相交且互相平分.
(2)由(1),AC∥MN.记平面MNP(即平面MNPQ)为α.显然ACα.
否则,若ACα,
由A∈α,M∈α,得B∈α;
由A∈α,Q∈α,得D∈α,则A、B、C、D∈α,
与已知四边形ABCD是空间四边形矛盾.
又∵MNα,∴AC∥α,
又AC α,∴AC∥α,即AC∥平面MNP.
同理可证BD∥平面MNP.
空间中的直线与平面1
知识梳理
例题解析
C
B
D
A
B1
C1
A1
D1
E
F
M
C
B
D
A
B1
C1
A1
D1
E
F
M
D
B1
A
C1
B
C
A1
D1
E
F
E
B
C
D
A
F
GF\
H
E
B
C
D
A
F
GF\
H
M
N
A
B
C
D
E
A1
B1
C1
D1
图7
C
D
A
B1
B
D1
A1
C1
E
F
A
C
B
P
A
S
T
Q
M
F
课后练习
B
A
D
C
P
N
Q
M
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
