人教高中数学选修2-2:1.5定积分的概念第二课时 课件(20张ppt)
文档属性
| 名称 | 人教高中数学选修2-2:1.5定积分的概念第二课时 课件(20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 725.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 21:09:33 | ||
图片预览





文档简介
(共20张PPT)
1.5 定积分的概念
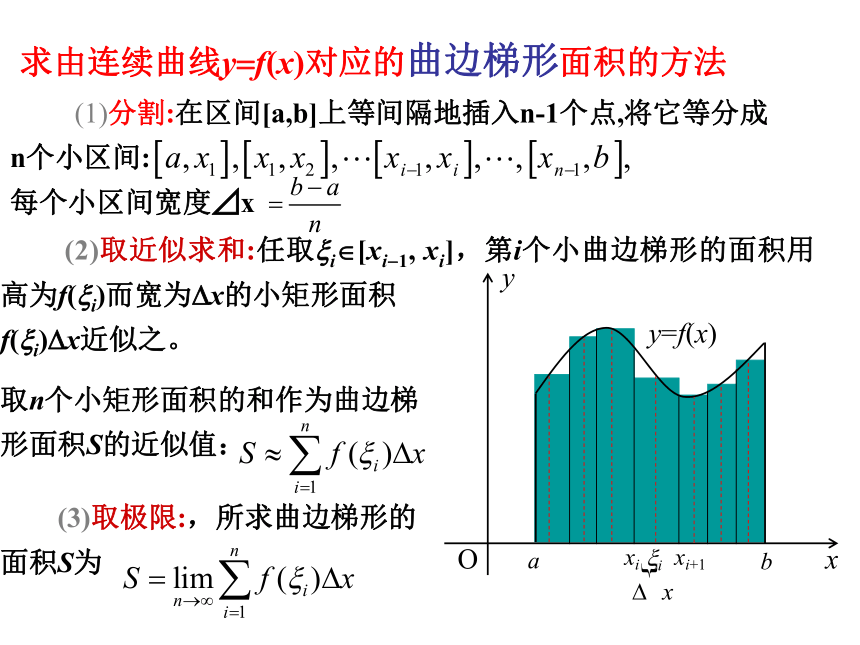
求由连续曲线y=f(x)对应的曲边梯形面积的方法
(2)取近似求和:任取xi?[xi-1, xi],第i个小曲边梯形的面积用高为f(xi)而宽为Dx的小矩形面积
f(xi)Dx近似之。
(3)取极限:,所求曲边梯形的面积S为
取n个小矩形面积的和作为曲边梯形面积S的近似值:
xi
xi+1
xi
定积分的定义
当n?∞时,Sn 就无限接近某个常数S,
这个常数为函数f(x)在区间[a, b]上的定积分,记作
从求曲边梯形面积S的过程中可以看出,通过“四步曲”:
分割---近似代替----求和------取极限得到解决.
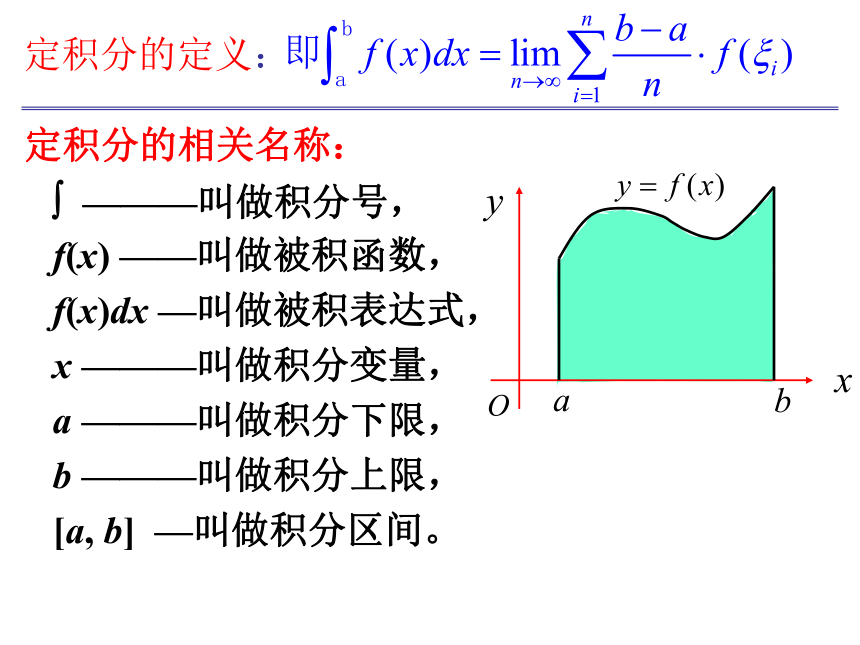
定积分的定义:
定积分的相关名称:
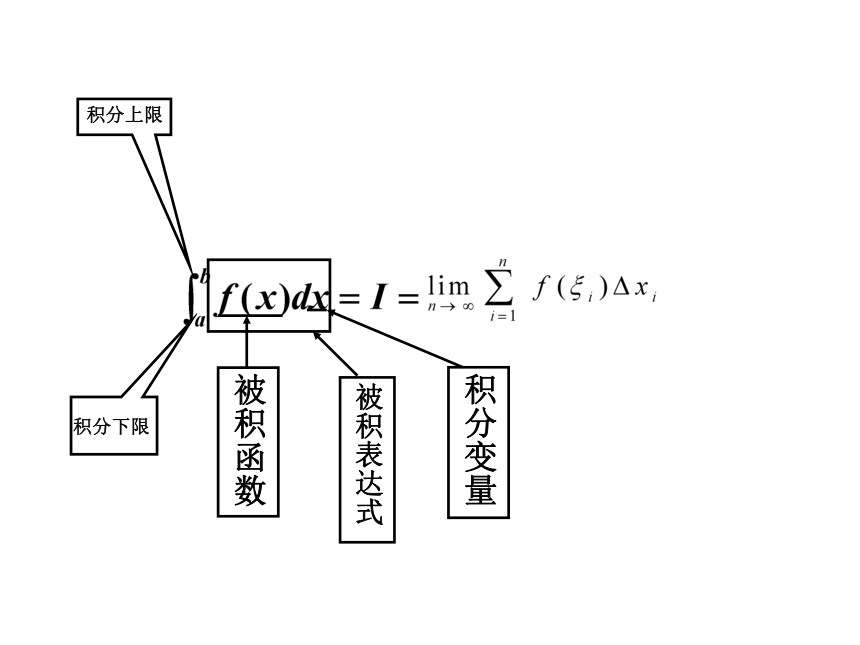
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。
积分下限
积分上限
说明:
(1) 定积分是一个数值,
它只与被积函数及积分区间有关,
而与积分变量的记法无关,即
(2)
例1:利用定积分的定义,计算
的值.
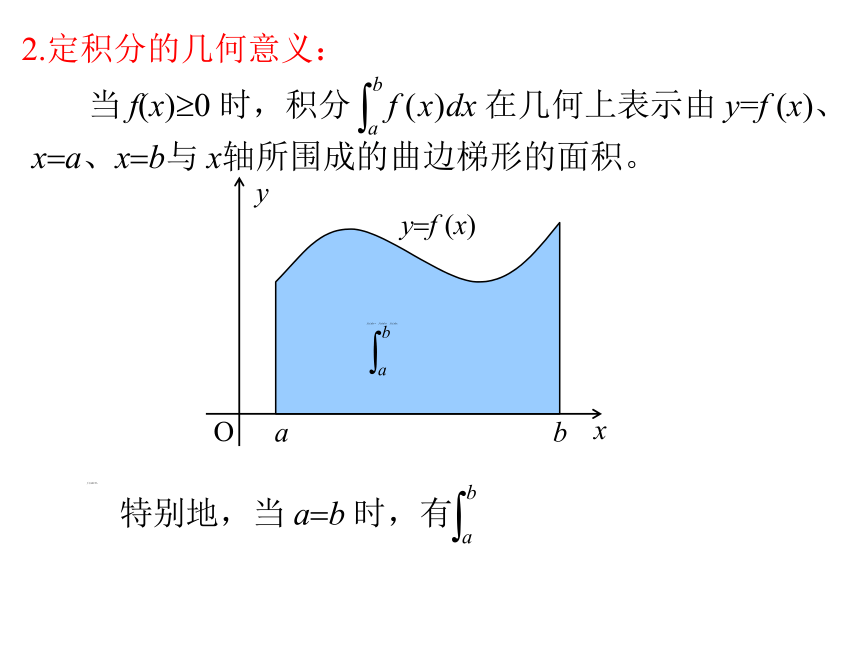
2.定积分的几何意义:
x=a、x=b与 x轴所围成的曲边梯形的面积。
当f(x)?0时,由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方,
上述曲边梯形面积的负值。
定积分的几何意义:
按定积分的定义,有
(1) 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积为
(2) 设物体运动的速度v=v(t),则此物体在时间区间[a, b]内运动的距离s为
定积分的定义:
1
例2.用定积分表示图中四个阴影部分面积
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
-1
2
a
b
-1
2
f(x)=x2
f(x)=x2
f(x)=1
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
-1
2
a
b
-1
2
f(x)=x2
f(x)=x2
f(x)=1
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
-1
2
a
b
-1
2
f(x)=x2
f(x)=x2
f(x)=1
f(x)=(x-1)2-1
例3
利用定积分的几何意义,判断下列定积分
值的正、负号。
利用定积分的几何意义,说明下列各式。
成立:
1).
2).
1).
2).
练习:
试用定积分表示下列各图中影阴部分的面积。
0
y
x
y=x2
1
2
0
x
y=f(x)
y=g(x)
a
b
y
3. 定积分的基本性质
性质1.
性质2.
定积分关于积分区间具有可加性
性质3.
例4:
解:
x
y
f(x)=sinx
1
-1
1.5 定积分的概念
求由连续曲线y=f(x)对应的曲边梯形面积的方法
(2)取近似求和:任取xi?[xi-1, xi],第i个小曲边梯形的面积用高为f(xi)而宽为Dx的小矩形面积
f(xi)Dx近似之。
(3)取极限:,所求曲边梯形的面积S为
取n个小矩形面积的和作为曲边梯形面积S的近似值:
xi
xi+1
xi
定积分的定义
当n?∞时,Sn 就无限接近某个常数S,
这个常数为函数f(x)在区间[a, b]上的定积分,记作
从求曲边梯形面积S的过程中可以看出,通过“四步曲”:
分割---近似代替----求和------取极限得到解决.
定积分的定义:
定积分的相关名称:
? ———叫做积分号,
f(x) ——叫做被积函数,
f(x)dx —叫做被积表达式,
x ———叫做积分变量,
a ———叫做积分下限,
b ———叫做积分上限,
[a, b] —叫做积分区间。
积分下限
积分上限
说明:
(1) 定积分是一个数值,
它只与被积函数及积分区间有关,
而与积分变量的记法无关,即
(2)
例1:利用定积分的定义,计算
的值.
2.定积分的几何意义:
x=a、x=b与 x轴所围成的曲边梯形的面积。
当f(x)?0时,由y?f (x)、x?a、x?b 与 x 轴所围成的曲边梯形位于 x 轴的下方,
上述曲边梯形面积的负值。
定积分的几何意义:
按定积分的定义,有
(1) 由连续曲线y=f(x) (f(x)?0) ,直线x=a、x=b及x轴所围成的曲边梯形的面积为
(2) 设物体运动的速度v=v(t),则此物体在时间区间[a, b]内运动的距离s为
定积分的定义:
1
例2.用定积分表示图中四个阴影部分面积
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
f(x)=x2
f(x)=x2
-1
2
f(x)=1
a
b
-1
2
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
-1
2
a
b
-1
2
f(x)=x2
f(x)=x2
f(x)=1
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
-1
2
a
b
-1
2
f(x)=x2
f(x)=x2
f(x)=1
f(x)=(x-1)2-1
解:
0
0
0
0
a
y
x
y
x
y
x
y
x
-1
2
a
b
-1
2
f(x)=x2
f(x)=x2
f(x)=1
f(x)=(x-1)2-1
例3
利用定积分的几何意义,判断下列定积分
值的正、负号。
利用定积分的几何意义,说明下列各式。
成立:
1).
2).
1).
2).
练习:
试用定积分表示下列各图中影阴部分的面积。
0
y
x
y=x2
1
2
0
x
y=f(x)
y=g(x)
a
b
y
3. 定积分的基本性质
性质1.
性质2.
定积分关于积分区间具有可加性
性质3.
例4:
解:
x
y
f(x)=sinx
1
-1
