沪科版数学七年级下册7.2一元一次不等式课件(共25张PPT)
文档属性
| 名称 | 沪科版数学七年级下册7.2一元一次不等式课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 21:35:02 | ||
图片预览






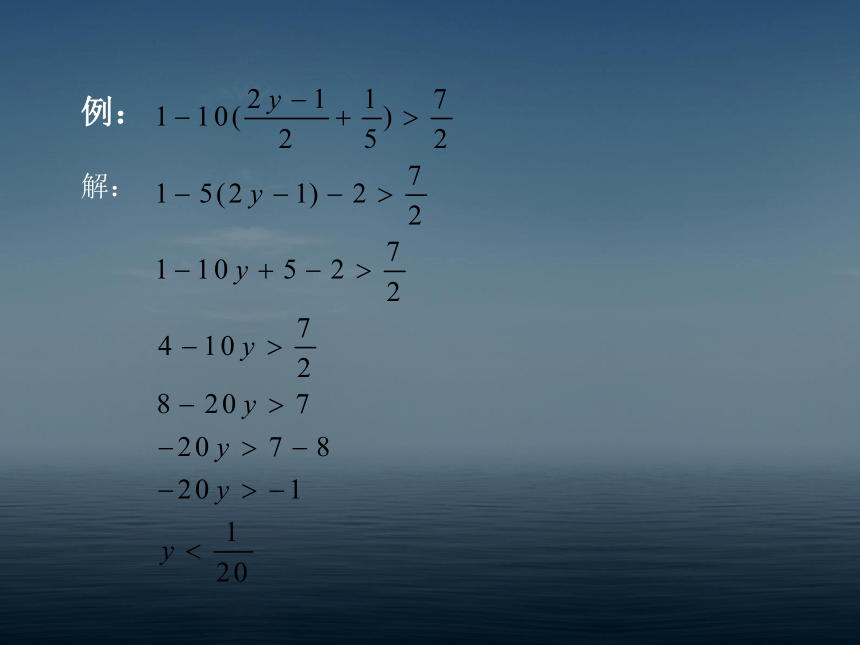


文档简介
(共25张PPT)
一元一次不等式
第七章:一元一次不等式及不等式组
第一节 解不等式
有关概念
1、什么是不等式? (什么是方程?)
2、什么是不等式的解? (什么是方程的解?)
3、什么是不等式的解集?
4、什么是解不等式? (什么是解方程?)
不等式的三个基本性质
1、不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
2、不等式两边都乘以(或除以)同一个正数,不等号的方向不变。
3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变。
例1 设a?b,下列各式中正确的是( )。
A a – 7?b?7 B ? 4a ? ? 4b
C D 6? 3a? 6?3b
例2 若a?b且ac≤ bc,则c的取值范围是( )。
A c ?0 B c≥0
C c ≤0 D c?0
A B C D
例3 如果a? b?0,那么下列各式中一定成立的是
( )。
解不等式的步骤:
1、去分母
2、去括号
3、移项
4、合并同类项
5、系数化为1
例:
解:
解不等式,并将解集在数轴上表示出来。
解题误区
0
11
22
正确解题
-2
-1
0
一元一次不等式与一元一次方程的区别和联系
一、概念的比较
区别:前者是用不等号将代数式连接而成,后者
是用等号将代数式连接而成,其余都相同
(1)都只含有一个未知数;
(2)含未知数的式子是整式;
(3)未知数的次数是1。
二、求解过程的比较
相同之处:
去分母、去括号、移项、合并同类项、系数化为1
不同之处:
在“去分母”与“系数化为1”时,方程两边都乘以(或除以)同一个正数或负数,等号不变。
不等式两边都乘以(或除以)同一个正数,不等号方向不变;不等式两边都乘以(或除以)同一个负数,不等号方向改变。
例:
解方程
解不等式
三、解的比较
一元一次方程的解只有一个;
一元一次不等式的解一般有无数个,它是在一定范围内的一系列数。
四、确定参数的比较
已知方程的解确定方程中的参数,可根据方程的解的意义,将解代入原方程便得到关于参数为元的新方程,解新方程可求得参数。
若已知不等式的解确定不等式中的参数,一般是先解不等式,与其比较后再确定参数。
例 已知关于x的方程 的解为2, 求a的值。
解:将x?2代入方程,得:2a?6?2?2,
解得:a?5
例 已知关于x的不等式 的解集为 x?2,求a的值。
解:解不等式 ,得(a?1)x?8,
与解集x>2比较得a?1>0且
解得a?5
练习:
1、比较大小:
(2)
(1)
( ? )
( ? )
2、判断下列说法是否正确:
(1)若a>b,则a?c>b?c.
(2)若a>b,则a >b .
(3)若a >b ,则a>b.
(4)若a>b,c>d,则ac>bd.
(5)若a>b,则 >
(6)若 则
(7)若 一定恒成立.
(8) 的解集一定是x>a.
3、判断下列说法是否正确:
(1) x?1是不等式-2x?1的解集.
(2) x?1是不等式- 2x?1的解.
(3) x? 是不等式- 2x?1的解.
(4) 不等式- 2x?1的解是x?1.
(5) x?2的整数解有无数个.
(6) x?3的正整数解有有限个.
4、解不等式
解:
(巧用整体性)
5、解不等式
解:
(巧用分数的基本性质)
解:将原不等式化为(a? 2)x>2(b+1)
当a?2? 0,即a ? 2时,不等式的解集为 .
当a?2?0,即a ? 2时,不等式的解集 为 .
当a?2=0,即a=2时,有
(1)若b ≥?1,不等式无解;
(2)若b 6、已知a,b为常数,解关于x的不等式
7.若 均为非负数, 则 的取值范围是( ).
解:将已知两等式化为
y?z?30?x,y?z?50?3x
∴2y?(30?x)?(50?3x),2z?(30?x)?(50?3x)
∴y?40?2x,z?x?10
∴M?5x?4(40?2x)?2(x?10)??x?140
∵x?0,y?0,z?0,
∴x?0,40?2x?0,x?10?0
∴10?x?20,?20??x??10
∴?20?140??x?140??10?140
∴120?M ? 130
8、设 则 的最大值与最小值之差为( )。
解:
的最小值为0,最大值为2。
所以原式的最大值是4,最小值是3,其差为1。
一元一次不等式
第七章:一元一次不等式及不等式组
第一节 解不等式
有关概念
1、什么是不等式? (什么是方程?)
2、什么是不等式的解? (什么是方程的解?)
3、什么是不等式的解集?
4、什么是解不等式? (什么是解方程?)
不等式的三个基本性质
1、不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变。
2、不等式两边都乘以(或除以)同一个正数,不等号的方向不变。
3、不等式两边都乘以(或除以)同一个负数,不等号的方向改变。
例1 设a?b,下列各式中正确的是( )。
A a – 7?b?7 B ? 4a ? ? 4b
C D 6? 3a? 6?3b
例2 若a?b且ac≤ bc,则c的取值范围是( )。
A c ?0 B c≥0
C c ≤0 D c?0
A B C D
例3 如果a? b?0,那么下列各式中一定成立的是
( )。
解不等式的步骤:
1、去分母
2、去括号
3、移项
4、合并同类项
5、系数化为1
例:
解:
解不等式,并将解集在数轴上表示出来。
解题误区
0
11
22
正确解题
-2
-1
0
一元一次不等式与一元一次方程的区别和联系
一、概念的比较
区别:前者是用不等号将代数式连接而成,后者
是用等号将代数式连接而成,其余都相同
(1)都只含有一个未知数;
(2)含未知数的式子是整式;
(3)未知数的次数是1。
二、求解过程的比较
相同之处:
去分母、去括号、移项、合并同类项、系数化为1
不同之处:
在“去分母”与“系数化为1”时,方程两边都乘以(或除以)同一个正数或负数,等号不变。
不等式两边都乘以(或除以)同一个正数,不等号方向不变;不等式两边都乘以(或除以)同一个负数,不等号方向改变。
例:
解方程
解不等式
三、解的比较
一元一次方程的解只有一个;
一元一次不等式的解一般有无数个,它是在一定范围内的一系列数。
四、确定参数的比较
已知方程的解确定方程中的参数,可根据方程的解的意义,将解代入原方程便得到关于参数为元的新方程,解新方程可求得参数。
若已知不等式的解确定不等式中的参数,一般是先解不等式,与其比较后再确定参数。
例 已知关于x的方程 的解为2, 求a的值。
解:将x?2代入方程,得:2a?6?2?2,
解得:a?5
例 已知关于x的不等式 的解集为 x?2,求a的值。
解:解不等式 ,得(a?1)x?8,
与解集x>2比较得a?1>0且
解得a?5
练习:
1、比较大小:
(2)
(1)
( ? )
( ? )
2、判断下列说法是否正确:
(1)若a>b,则a?c>b?c.
(2)若a>b,则a >b .
(3)若a >b ,则a>b.
(4)若a>b,c>d,则ac>bd.
(5)若a>b,则 >
(6)若 则
(7)若 一定恒成立.
(8) 的解集一定是x>a.
3、判断下列说法是否正确:
(1) x?1是不等式-2x?1的解集.
(2) x?1是不等式- 2x?1的解.
(3) x? 是不等式- 2x?1的解.
(4) 不等式- 2x?1的解是x?1.
(5) x?2的整数解有无数个.
(6) x?3的正整数解有有限个.
4、解不等式
解:
(巧用整体性)
5、解不等式
解:
(巧用分数的基本性质)
解:将原不等式化为(a? 2)x>2(b+1)
当a?2? 0,即a ? 2时,不等式的解集为 .
当a?2?0,即a ? 2时,不等式的解集 为 .
当a?2=0,即a=2时,有
(1)若b ≥?1,不等式无解;
(2)若b 6、已知a,b为常数,解关于x的不等式
7.若 均为非负数, 则 的取值范围是( ).
解:将已知两等式化为
y?z?30?x,y?z?50?3x
∴2y?(30?x)?(50?3x),2z?(30?x)?(50?3x)
∴y?40?2x,z?x?10
∴M?5x?4(40?2x)?2(x?10)??x?140
∵x?0,y?0,z?0,
∴x?0,40?2x?0,x?10?0
∴10?x?20,?20??x??10
∴?20?140??x?140??10?140
∴120?M ? 130
8、设 则 的最大值与最小值之差为( )。
解:
的最小值为0,最大值为2。
所以原式的最大值是4,最小值是3,其差为1。
