人教版数学八年级下册18.2.3正方形课件(共36张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.2.3正方形课件(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 21:45:53 | ||
图片预览









文档简介
(共36张PPT)
义务教育人教版中学数学
18.2.3正方形
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
1. 理解并掌握正方形的概念、性质;
2. 经历探索正方形有关性质的过程,理解正方形与平行四边形、矩形、菱形之间的联系和区别.
学习目标:
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
矩形
角:
四个角是直角
对角线:
对角线相等
边:
具有平行四边形所有性质
菱形
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
具有平行四边形一切性质
角:
同学们手里有一个矩形,你能剪一刀变成一个正方形吗?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
有一组邻边相等
探 究(二)
你能把这个菱形变化成一个正方形吗?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形
菱形
正方形
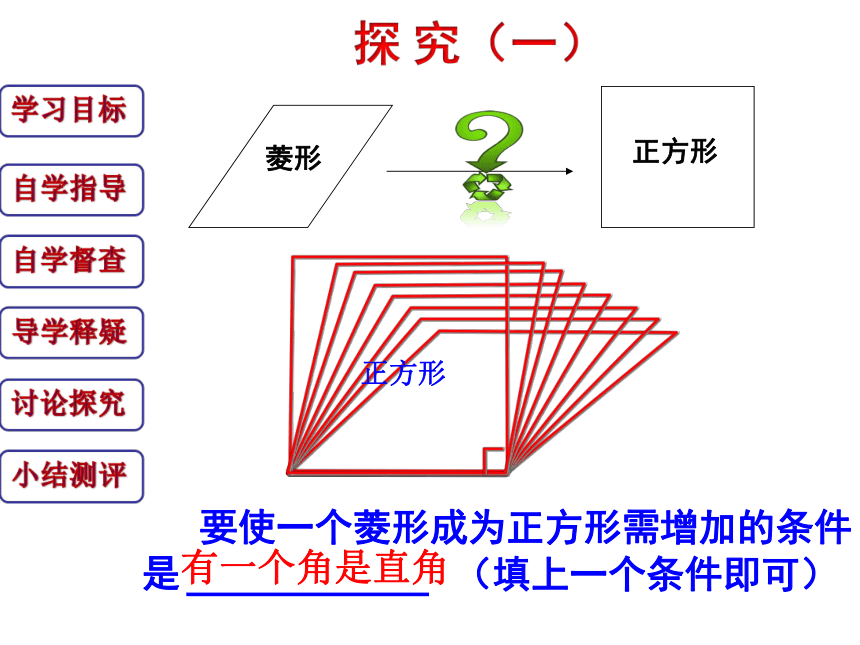
探 究(一)
要使一个菱形成为正方形需增加的条件是
(填上一个条件即可)
有一个角是直角
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
★ 正方形是特殊的矩形
★ 正方形是特殊的菱形
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形既是特殊的矩形
又是特殊的菱形.
正方形具有矩形性质的同时也具有菱形的性质.
性 质
边 角 对角线 对称性
图形语言
文字语言
几何语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形
菱形的性质
矩形的性质
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
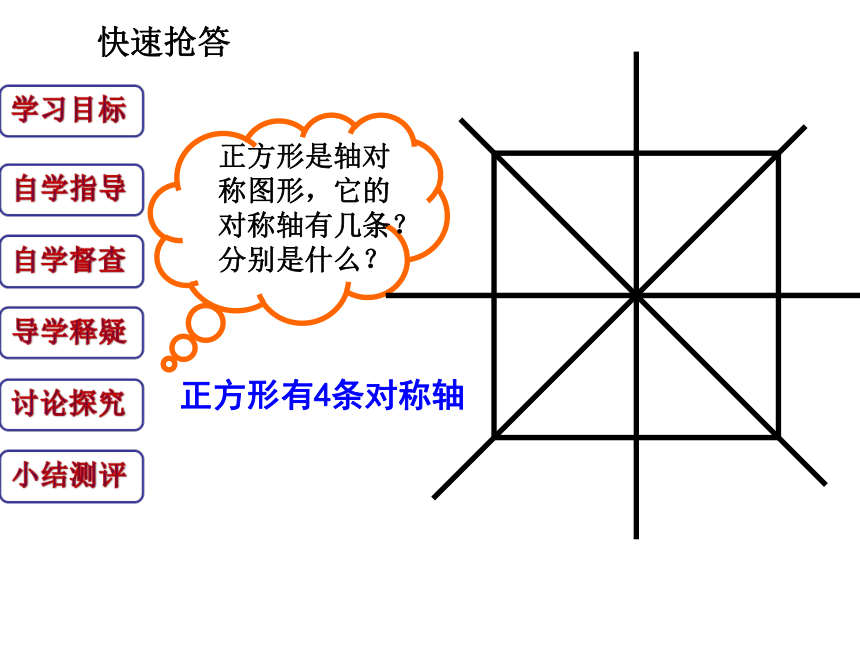
正方形是轴对称图形,它的对称轴有几条?分别是什么?
快速抢答
正方形有4条对称轴
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
3.正方形ABCD的面积是9cm2。则AB=________AC=___________
1.一正方形边长为4,则它的面积为 .
2.一正方形对角线长为4,则它的面积为 .
A
B
C
D
16
8
3cm
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
你觉得什么样的四边形是正方形呢?( 判断一个四边形是正方形有哪些方法?)
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形的判定
正方形
菱形
有一个角是直角
矩形
一组邻边相等
正方形
或 对角线垂直
或 对角线相等
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
√
×
×
√
√
1.对角线相等的菱形是正方形( )
2.对角线互相垂直的矩形是正方形( )
3.对角线互相垂直且相等的四边形是正方形
( )
4.四条边都相等的四边形是正方形( )
5.四个角都相等的四边形是正方形( )
4.判断
×
6.四边相等,有一个角是直角的四边形是正方形 ( )
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
5、已知四边形ABCD是平行四边形,对角线AC、BD相交于点O。
(1)若AB=BC,则四边形ABCD是( )
(2)若AC=BD,则四边形ABCD是( )
(3)若OA=OB,则四边形ABCD是( )
(4)若AB=BC,且AC=BD,则四边形ABCD是( )
A
B
C
D
O
菱形
矩形
矩形
正方形
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
6.如图,正方形ABCD中,E,F,G,H分别是各边上的点,且AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
E
A
B
C
D
F
H
G
2╰
1
╮
╯
3
╮
4
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
总结反思
你有何收获呢?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
A
B
C
E
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=30m,EB=10m
∴正方形ABCD面积=( )2=800(m2)
∴
∴
D
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
课后作业
【必做题】
教材59页:练习题1、2
教材67页:1题
教材68页:8题
【选做题】
教材62页:15题
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )
A.①②③ B.①② C.①③ D.②③
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
矩形、菱形、正方形都具有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线平分一组对角
D.对角线互相垂直
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
若正方形的对角线长是6,则此正方形的面积是____.
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B.15
C.16 D.17
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
两个边长均为2的正方形如图所示放置,正方形ABCD的对角线相较于点O,点O同时又是正方形EFGO的一个顶点,则两个正方形重合的部分面积是多少呢?
A
D
B
C
O
E
F
G
M
N
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
A
D
B
C
O
E
F
G
【变式】若将正方形OEFG按逆时针旋转一定的角度,其他条件不变,上题中的结论仍成立吗?请说明理由。
M
N
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
2╰
1
╮
╯
3
╮
4
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
合作探究
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
问题:
1. 图中CD在平移时,这个图形始终是怎样的图形?
2. 当CD移动到C?D?位置,此时AD?=AB,四边形ABCD还是矩形吗?
A
B
C
D
A
B
C?
D?
探 究(二)
你觉得什么样的四边形是正方形呢?
某一拉门在完全关闭时,其相应的菱形变成什么图形了呢?
1
1
义务教育人教版中学数学
18.2.3正方形
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
1. 理解并掌握正方形的概念、性质;
2. 经历探索正方形有关性质的过程,理解正方形与平行四边形、矩形、菱形之间的联系和区别.
学习目标:
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
矩形
角:
四个角是直角
对角线:
对角线相等
边:
具有平行四边形所有性质
菱形
边:
四条边相等
对角线:
互相垂直
分别平分两组对角
具有平行四边形一切性质
角:
同学们手里有一个矩形,你能剪一刀变成一个正方形吗?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
矩 形
正方形
〃
〃
矩形怎样变化后就成了正方形呢?
要使一个矩形成为正方形需添加的条件是
(填上一个条件即可)
有一组邻边相等
探 究(二)
你能把这个菱形变化成一个正方形吗?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形
菱形
正方形
探 究(一)
要使一个菱形成为正方形需增加的条件是
(填上一个条件即可)
有一个角是直角
探究小结
矩 形
〃
〃
正方形
邻边
相等
〃
〃
发现:
一组邻边相等的矩形 是正方形
菱 形
一个角
是直角
正方形
∟
发现:
一个角为直角的菱形是正方形
★ 正方形是特殊的矩形
★ 正方形是特殊的菱形
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形既是特殊的矩形
又是特殊的菱形.
正方形具有矩形性质的同时也具有菱形的性质.
性 质
边 角 对角线 对称性
图形语言
文字语言
几何语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形
菱形的性质
矩形的性质
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形是轴对称图形,它的对称轴有几条?分别是什么?
快速抢答
正方形有4条对称轴
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
3.正方形ABCD的面积是9cm2。则AB=________AC=___________
1.一正方形边长为4,则它的面积为 .
2.一正方形对角线长为4,则它的面积为 .
A
B
C
D
16
8
3cm
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
你觉得什么样的四边形是正方形呢?( 判断一个四边形是正方形有哪些方法?)
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
正方形的判定
正方形
菱形
有一个角是直角
矩形
一组邻边相等
正方形
或 对角线垂直
或 对角线相等
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
√
×
×
√
√
1.对角线相等的菱形是正方形( )
2.对角线互相垂直的矩形是正方形( )
3.对角线互相垂直且相等的四边形是正方形
( )
4.四条边都相等的四边形是正方形( )
5.四个角都相等的四边形是正方形( )
4.判断
×
6.四边相等,有一个角是直角的四边形是正方形 ( )
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
5、已知四边形ABCD是平行四边形,对角线AC、BD相交于点O。
(1)若AB=BC,则四边形ABCD是( )
(2)若AC=BD,则四边形ABCD是( )
(3)若OA=OB,则四边形ABCD是( )
(4)若AB=BC,且AC=BD,则四边形ABCD是( )
A
B
C
D
O
菱形
矩形
矩形
正方形
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
6.如图,正方形ABCD中,E,F,G,H分别是各边上的点,且AE=BF=CG=DH.四边形EFGH是正方形吗?为什么?
E
A
B
C
D
F
H
G
2╰
1
╮
╯
3
╮
4
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
平行四边形
矩形
菱形
正
方
形
正方形、菱形、矩形、平行四边形四者之间有什么关系?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
总结反思
你有何收获呢?
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
如图,ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=30m,EB=10m,这块场地的面积和对角线长分别是多少?
A
B
C
E
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=30m,EB=10m
∴正方形ABCD面积=( )2=800(m2)
∴
∴
D
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
课后作业
【必做题】
教材59页:练习题1、2
教材67页:1题
教材68页:8题
【选做题】
教材62页:15题
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )
A.①②③ B.①② C.①③ D.②③
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
矩形、菱形、正方形都具有的性质是( )
A.对角线相等
B.对角线互相平分
C.对角线平分一组对角
D.对角线互相垂直
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
若正方形的对角线长是6,则此正方形的面积是____.
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
如图,正方形ABCD中,对角线AC,BD相交于点O,则图中的等腰三角形有( )
A.4个 B.6个 C.8个 D.10个
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B.15
C.16 D.17
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
两个边长均为2的正方形如图所示放置,正方形ABCD的对角线相较于点O,点O同时又是正方形EFGO的一个顶点,则两个正方形重合的部分面积是多少呢?
A
D
B
C
O
E
F
G
M
N
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
A
D
B
C
O
E
F
G
【变式】若将正方形OEFG按逆时针旋转一定的角度,其他条件不变,上题中的结论仍成立吗?请说明理由。
M
N
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗?为什么?
A
B
C
D
E
F
G
H
2╰
1
╮
╯
3
╮
4
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
合作探究
学习目标
自学指导
导学释疑
自学督查
讨论探究
小结测评
问题:
1. 图中CD在平移时,这个图形始终是怎样的图形?
2. 当CD移动到C?D?位置,此时AD?=AB,四边形ABCD还是矩形吗?
A
B
C
D
A
B
C?
D?
探 究(二)
你觉得什么样的四边形是正方形呢?
某一拉门在完全关闭时,其相应的菱形变成什么图形了呢?
1
1
