苏教版高二数学选修2-2 3.3复数的几何意义(1)(共19张PPT)
文档属性
| 名称 | 苏教版高二数学选修2-2 3.3复数的几何意义(1)(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 305.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 20:47:39 | ||
图片预览




文档简介
(共19张PPT)
复数的几何意义(1)
扬州市江都区大桥高级中学
1. 对虚数单位i 的规定
① i 2=-1;
②可以与实数一起进行四则运算.
2. 复数z=a+bi(其中a、b?R)中a叫z 的 、 b叫z的 .
实部
虚部
z为实数? 、z为纯虚数? .
b=0
练习:把下列运算的结果都化为 a+bi(a、b?R)的形式.
2 -i = ;-2i = ;5= ;0= ;
3. a=0是z=a+bi(a、b?R)为纯虚数的 条件.
必要不充分
课前复习
在几何上,我们用什么来表示实数?
想一想?
问题情境
类比实数的表示,可以用什么来表示复数?
实数可以用数轴上的点来表示.
实数
数轴上的点
(形)
(数)
一一对应
回忆…
复数的一般形式?
实部!
虚部!
一个复数由什么唯一确定?
Z=a+bi(a,b∈R)
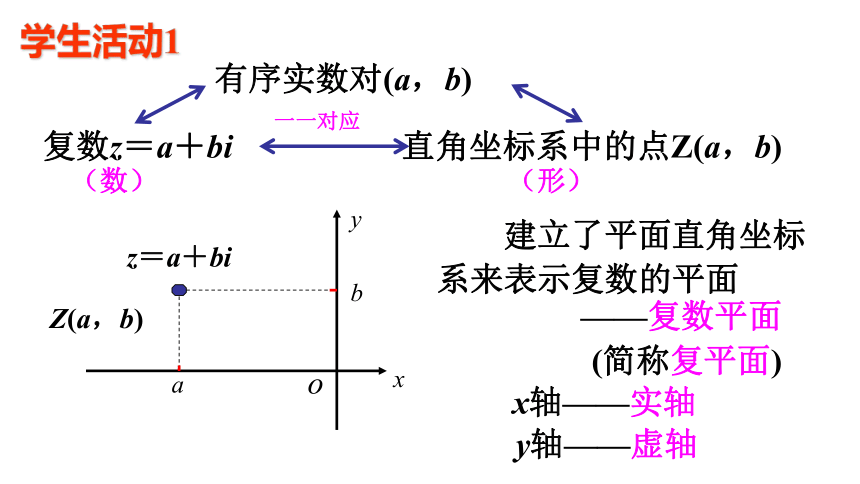
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x
y
o
b
a
Z(a,b)
建立了平面直角坐标系来表示复数的平面
x轴——实轴
y轴——虚轴
(数)
(形)
——复数平面 (简称复平面)
一一对应
z=a+bi
学生活动1
例1
在复平面内,分别用点表示下列复数.
4,2+i,-i,-1+3i,3-2i
思考 1.复平面内,表示一对共轭虚数的两个点具有怎样的位置关系?
2.如果复平面内表示两个虚数的点关于原点对称,那么它们的实部和虚部分别满足什么关系?
(A)在复平面内,对应于实数的点都在实轴上;
(B)在复平面内,对应于纯虚数的点都在虚轴上;
(C)在复平面内,实轴上的点所对应的复数都是实数;
(D)在复平面内,虚轴上的点所对应的复数都是纯虚数.
3.下列命题中的假命题是( )
D
实轴上的点都表示实数
除原点外,虚轴上的点都表示纯虚数数
例2 已知复数z=(m2+m-6) +(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围.
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值.
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-6)-2(m2+m-2)+4=0,
∴m=1或m=-2.
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
一一对应
一一对应
学生活动2
x
y
o
b
a
Z(a,b)
z=a+bi
平面向量
例1
在复平面内,分别用向量表示下列复数.
4,2+i,-i,-1+3i,3-2i
想一想?
实数绝对值的几何意义是什么?
能否类比定义复数的绝对值?
实数绝对值的几何意义:
复数的模其实是实数绝对值概念的推广
x
O
A
a
|a| = |OA|
实数a在数轴上所对应的点A到原点O的距离.
x
O
z=a+bi
y
|z|=|OZ|
复数的模
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
的几何意义:
Z(a,b)
复数的模
的几何意义:
│z│=│ │
│ │三者有何关系?
例3 已知复数
思考 任意两个复数都可以比较大小吗?
试比较它们模的大小.
能比较大小的复数肯定是实数
练习
课堂小结
1.复数的几何意义.
2.数形结合的思想方法.
谢谢大家!
复数的几何意义(1)
扬州市江都区大桥高级中学
1. 对虚数单位i 的规定
① i 2=-1;
②可以与实数一起进行四则运算.
2. 复数z=a+bi(其中a、b?R)中a叫z 的 、 b叫z的 .
实部
虚部
z为实数? 、z为纯虚数? .
b=0
练习:把下列运算的结果都化为 a+bi(a、b?R)的形式.
2 -i = ;-2i = ;5= ;0= ;
3. a=0是z=a+bi(a、b?R)为纯虚数的 条件.
必要不充分
课前复习
在几何上,我们用什么来表示实数?
想一想?
问题情境
类比实数的表示,可以用什么来表示复数?
实数可以用数轴上的点来表示.
实数
数轴上的点
(形)
(数)
一一对应
回忆…
复数的一般形式?
实部!
虚部!
一个复数由什么唯一确定?
Z=a+bi(a,b∈R)
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
x
y
o
b
a
Z(a,b)
建立了平面直角坐标系来表示复数的平面
x轴——实轴
y轴——虚轴
(数)
(形)
——复数平面 (简称复平面)
一一对应
z=a+bi
学生活动1
例1
在复平面内,分别用点表示下列复数.
4,2+i,-i,-1+3i,3-2i
思考 1.复平面内,表示一对共轭虚数的两个点具有怎样的位置关系?
2.如果复平面内表示两个虚数的点关于原点对称,那么它们的实部和虚部分别满足什么关系?
(A)在复平面内,对应于实数的点都在实轴上;
(B)在复平面内,对应于纯虚数的点都在虚轴上;
(C)在复平面内,实轴上的点所对应的复数都是实数;
(D)在复平面内,虚轴上的点所对应的复数都是纯虚数.
3.下列命题中的假命题是( )
D
实轴上的点都表示实数
除原点外,虚轴上的点都表示纯虚数数
例2 已知复数z=(m2+m-6) +(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围.
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
变式一:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点在直线x-2y+4=0上,求实数m的值.
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-6)-2(m2+m-2)+4=0,
∴m=1或m=-2.
复数z=a+bi
直角坐标系中的点Z(a,b)
一一对应
一一对应
一一对应
学生活动2
x
y
o
b
a
Z(a,b)
z=a+bi
平面向量
例1
在复平面内,分别用向量表示下列复数.
4,2+i,-i,-1+3i,3-2i
想一想?
实数绝对值的几何意义是什么?
能否类比定义复数的绝对值?
实数绝对值的几何意义:
复数的模其实是实数绝对值概念的推广
x
O
A
a
|a| = |OA|
实数a在数轴上所对应的点A到原点O的距离.
x
O
z=a+bi
y
|z|=|OZ|
复数的模
复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
的几何意义:
Z(a,b)
复数的模
的几何意义:
│z│=│ │
│ │三者有何关系?
例3 已知复数
思考 任意两个复数都可以比较大小吗?
试比较它们模的大小.
能比较大小的复数肯定是实数
练习
课堂小结
1.复数的几何意义.
2.数形结合的思想方法.
谢谢大家!
