沪教版数学高二下春季班:第八讲多面体的表面积与体积 同步学案(教师版)
文档属性
| 名称 | 沪教版数学高二下春季班:第八讲多面体的表面积与体积 同步学案(教师版) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
沪教版数学高二下春季班第八讲
课题 多面体的表面积与体积 单元 第十五章 学科 数学 年级 十一
学习 目标 1.掌握棱拄、棱锥侧面积的计算方法; 2.掌握棱拄、棱锥体积的计算方法.
重点 1.掌握棱拄、棱锥侧面积的常见类型的计算方法; 2.掌握棱柱、棱锥体积的常见类型的计算方法.
难点 掌握棱柱、棱锥体积的常见类型的计算方法.
教学安排
版块 时长
1 知识梳理 30
2 例题解析 60
3 巩固训练 20
4 师生总结 10
5 课后练习 30
多面体的定义:由几个多边形围成的封闭立体叫多面体。
棱柱
定义:两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面围成的多面体叫做棱柱。棱柱的互相平行的两个面叫做棱柱的底面,其余各面叫做棱柱的侧面,相邻的两个侧面的公共边叫做棱柱的侧棱,两个底面间的距离叫做棱柱的高。
基本性质:侧面都是平行四边形;两个底面及平行于底面的截面都是全等的多边形;过不相邻的两条侧棱的截面是平行四边形。
棱柱的分类:侧棱与底面不垂直的的棱柱叫做斜棱柱;侧棱与底面垂直的棱柱叫做直棱柱;底面是正多边形的直棱柱叫做正棱柱。直棱柱侧面都是矩形;直棱柱侧棱与高相等;正棱柱的侧面都是全等的矩形。底面是平行四边形的棱柱叫做平行六面体;底面是矩形的直棱柱是长方体。
祖暅原理:夹在两个平行平面间的两个几何体,如果被平行于这两个平面的任何平面所截得的两个截面的面积都相等,那么这两个几何体的体积相等。
侧面积和体积公式:(为垂直于侧棱的直截面的周长,为侧棱长),(为底面面积,为高)
棱锥
定义:有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。棱锥的这个多边形的面叫做底面,其余各个三角形的面叫做侧面。相邻的两个侧面的公共边叫做棱锥的侧棱。各个侧面的公共顶点叫做棱锥的顶点,顶点到底面的距离叫做棱锥的高。
基本性质:如果一个棱锥被平行于底面的一个平面所截,那么侧棱和高被这个平面分成比例线段;截面与底面都是相似多边形;截面面积与底面面积之比,等于顶点到截面与顶点到底面的距离平方之比。
正棱锥
定义:如果一个棱锥的底面是多边形,且顶点在诺面的射影是底面的中心,这个棱锥叫做正棱锥;
基本性质:各侧棱相等,各侧面都是全等的等腰三角形;正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
面积与体积:,。
1、多面体的表面积
【例1】⑴棱柱的侧面是 形;
⑵直棱柱的侧面是 形;
⑶正棱柱的侧面是 形;
⑷正棱锥的侧面是 形;
⑸ ;其中 .
⑹正棱锥的侧面积公式是 ;其中 .
【难度】★
【答案】平行四边;矩;全等的矩;全等的等腰三角;,是底面周长,是直棱柱的高;,
是底面周长,是棱锥的斜高.
【例2】三棱锥V-ABC中, AB=AC=10,BC=12,各侧面与底面成的二面角都是45°,求三棱锥的高及侧面积?
【难度】★★
【答案】取中点,连接,,
,,
各侧面与底面成的二面角都是45°,设二面角;
设,各侧面与底面成的二面角都是45°,即是的内心,设半径为,则,,
【例3】如图,已知正三棱柱的底面边长为2,高为5 ,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为________.
【难度】★★
【答案】13
【解析】根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为=13 ().
【例4】三棱锥中,,,求该棱锥的表面积.
【难度】★★
【答案】
【解析】取中点,连结。∵,∴。同理,。
故平面。在正三角形中,,同理。
取中点,连结,则。∴,
。
又,连结,,∴。∴。
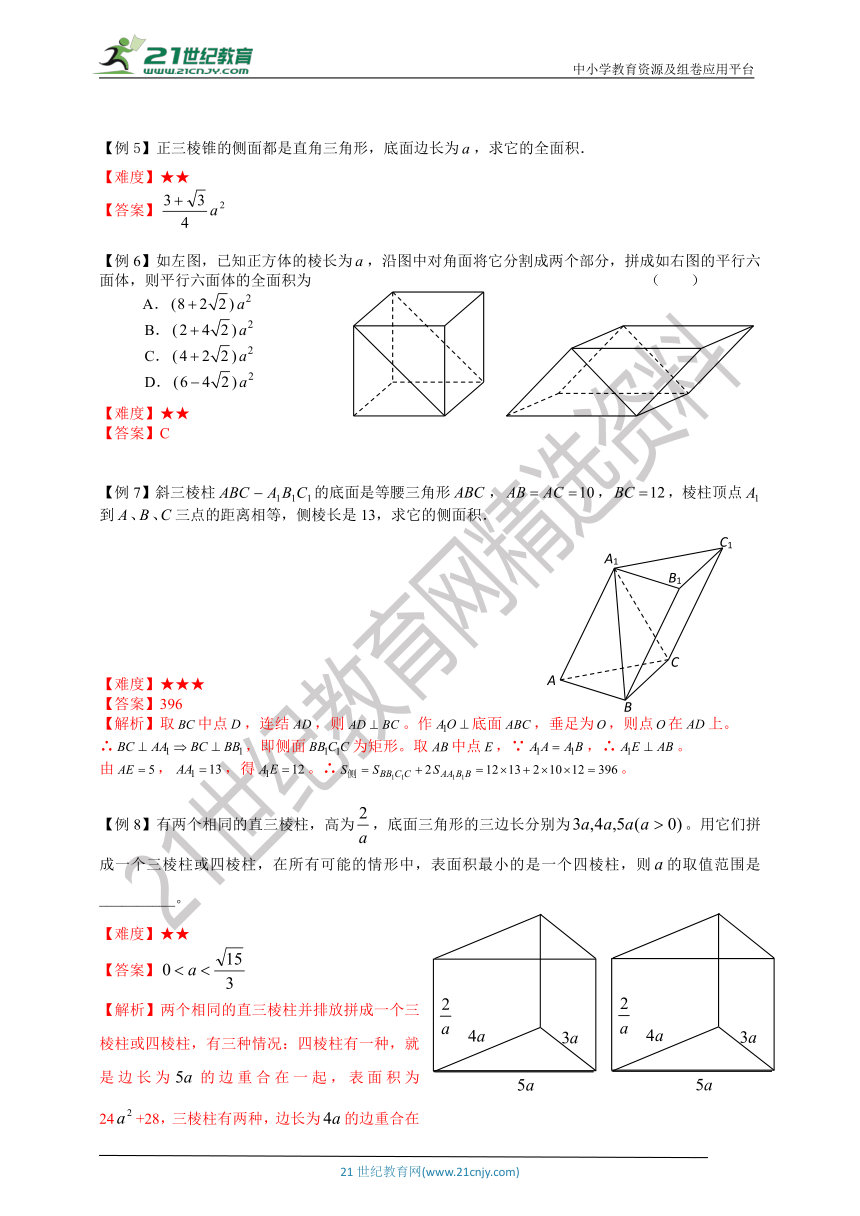
【例5】正三棱锥的侧面都是直角三角形,底面边长为,求它的全面积.
【难度】★★
【答案】
【例6】如左图,已知正方体的棱长为,沿图中对角面将它分割成两个部分,拼成如右图的平行六面体,则平行六面体的全面积为 ( )
A.
B.
C.
D.
【难度】★★
【答案】C
【例7】斜三棱柱的底面是等腰三角形,,,棱柱顶点
到三点的距离相等,侧棱长是13,求它的侧面积.
【难度】★★★
【答案】396
【解析】取中点,连结,则。作底面,垂足为,则点在上。
∴,即侧面为矩形。取中点,∵,∴。
由,,得。∴。
【例8】有两个相同的直三棱柱,高为,底面三角形的三边长分别为。用它们拼成一个三棱柱或四棱柱,在所有可能的情形中,表面积最小的是一个四棱柱,则的取值范围是__________。
【难度】★★
【答案】
【解析】两个相同的直三棱柱并排放拼成一个三棱柱或四棱柱,有三种情况:四棱柱有一种,就是边长为的边重合在一起,表面积为24+28,三棱柱有两种,边长为的边重合在一起,表面积为24+32,边长为的边重合在一起,表面积为24+36 ,两个相同的直三棱柱竖直放在一起,有一种情况表面积为12+48。最小的是一个四棱柱,这说明
【巩固训练】
1.若正棱锥的底面边长与侧棱长相等,则该棱锥一定不是 ( )
A.三棱锥 B.三棱锥 C.五棱锥 D.六棱锥
【难度】★
【答案】D
2.正四棱锥的侧棱和底面边长都是,则它的全面积是____________.
【难度】★★
【答案】
3.正方体的八个顶点中有四个恰为一个正四面体的顶点,则正方体的全面积与该正四面体的全面积之比为 ( )
A. B. C. D.
【难度】★★
【答案】C
4.斜三棱柱的底面是正三角形,侧棱和棱所成的角都是,若,则此三棱锥的全面积为________________.
【难度】★★
【答案】
5.已知长方体中,从点出发沿着表面运动到的最短路线长是多少?
【难度】★★
【答案】
6.如图,在正四棱柱中,AB=1,,点E为AB上的动点,则的最小值为( )
A. B. C. D.
【难度】★★
【答案】B
【解析】将正方形ABCD沿AB向下翻折到对角面ABC1D1内成为正方形ABC2D2,在矩形C1D1D2C2中连接D1C2,与AB的交点即为所求最小值点E,此时D1E+CE=D1C2.因为对角线BC1=2,C1C2=3,故
7.如图是某几何体的三视图(单位:m),则其表面积为_______.
【难度】★★★
【答案】
多面体的体积
【例9】⑴两个等底等高的棱柱体积之间的关系是 ;
⑵等底等高的三棱锥体积是三棱柱体积的 ;
⑶一个棱锥(),可以分割成与原棱锥共顶点且等高的 个三棱锥;
⑷棱锥的体积公式是 ;其中 ;
⑸三棱锥的三个侧面两两垂直,其面积分别为,则该三棱锥的体积为_______.
【难度】★
【答案】相等;;;,是底面面积,是高;.
【例10】正方体棱长为,分别是的中点.求
(1)三棱锥的体积;
(2)三棱锥的体积;
(3)四棱锥的体积.
【难度】★★
【答案】(1);(2);(3).
【例11】已知正四面体的棱长为,求
(1)此正四面体的高和斜高;
(2)此正四面体的体积和表面积;
(3)侧面和底面所成二面角的大小;
(4)侧棱和底面所成角的大小.
【难度】★★
【答案】(1);(2);(3);(4)
【例12】用一块钢锭浇注一个厚度均匀,且全面积为2平方米的正四棱锥有盖容器(如图),设容器的高为米,盖子边长为米.
(1)求关于的函数解析式;
(2)设容器的容积为立方米,当为何值时,最大?并求出的最大值(不计容器的厚度) .
【难度】★★
【答案】见解析
【解析】作平面,垂足为。作于,连结,则。
∵,∴,解之,得
。
(2),当且仅当时等号成立。
即棱锥的高为1米,底面边长为米时,立方米。
【例13】三棱锥中,,且与底面成角.
(1)求证是直角三角形;
(2)求该三棱锥体积的最大值.
【难度】★★
【答案】见解析
【解析】(1)设在底面的射影为,则为的外心,且。
∴为中点,故是以为直角的直角三角形。
(2)。
此时是等腰直角三角形。
也可设,则,当时,。
此时。
【例14】我们可以运用下面的原理解决一些相关图形的面积问题:如果与一固定直线平行的直线被甲、乙两个封闭图形所截得线段的比为定值,那么
甲的面积是乙的面积的倍。你可以从给出
的简单图形①(甲:大矩形、乙:
小矩形)、②(甲:大直角三角形
乙:小直角三角形)中体会
这个原理,现在图③中的曲线分别是
与,
运用上面的原理,求图③中椭圆的面积.
【难度】★★★
【答案】.
【例15】若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为60°的菱形,则该棱柱的体积为
【难度】★★
【答案】如图,依题意可知,为棱长为2的正四面体,过点作的高,与交于D,
【例16】已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是,则正视图中的等于_____.
【难度】★★
【答案】20
【例17】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为的正方形,高为,内有深的溶液.现将此容器倾斜一定角度(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(1)要使倾斜后容器内的溶液不会溢出,角的最大值是多少;
(2)现需要倒出不少于的溶液,当时,能实现要求吗?请说明理由.
【难度】★★
【答案】(1)如图③,当倾斜至上液面经过点时,容器内溶液恰好不会溢出,此时最大.
解法一:此时,梯形的面积等于(),
因为,所以,,
即,解得,.
所以,要使倾斜后容器内的溶液不会溢出,的最大值是.
解法二:此时,△的面积等于图①中没有液体部分的面积,
即(),
因为,所以,即,
解得,.
所以,要使倾斜后容器内的溶液不会溢出,的最大值是.
(2)如图④,当时,设上液面为,因为,
所以点在线段上,
此时,,
(),
剩余溶液的体积为(),
由题意,原来溶液的体积为,
因为,所以倒出的溶液不满.
所以,要倒出不少于的溶液,当时,不能实现要求.
【例18】在三棱锥中,且 .
求证并求三棱锥的体积.
【难度】★★
【答案】因为,,所以平面,所以.又.所以平面.故.
在中,,所以.
又在中,,所以.
又因为平面,所以
【巩固训练】
1.若一个长方体的全面积是,体积是,则这样的长方体的个数是_________.
【难度】★★
【答案】0
2.已知正六棱柱的较长的对角线长为,较短的对角线与底面所成的角为,求该棱柱的体积.
【难度】★★
【答案】
3.如图所示,在平行六面体ABCD—A1B1C1D1中,已知AB=5,AD=4,AA1=3,AB⊥AD,∠A1AB=∠A1AD=.
(1)求证:顶点A1在底面ABCD上的射影O在∠BAD的平分线上;
(2)求这个平行六面体的体积.
【难度】★★★
【答案】
【解析】(1)如图,连结A1O,则A1O⊥底面ABCD。作OM⊥AB交AB于M,作ON⊥AD交AD于N,连结A1M,A1N。由三垂线定得得A1M⊥AB,A1N⊥AD。∵∠A1AM=∠A1AN,
∴Rt△A1NA≌Rt△A1MA,∴A1M=A1N,
从而OM=ON。
∴点O在∠BAD的平分线上。
(2)∵AM=AA1cos=3×=
∴AO==。
又在Rt△AOA1中,A1O2=AA12 – AO2=9-=,
∴A1O=,平行六面体的体积为。
4.在棱长为的正方体中,是的中点, 若都是上的点, 且,是上的点, 则四面体的体积是 ;
【难度】★★
【答案】
5.三棱锥中,、、、分别为、、、的中点,则截面将三棱锥分成两部分的体积之比为_____________
【难度】★★
【答案】
6.如图,在边长为4的正方形纸片中,与相交于,剪去,将剩余部分沿,折叠,使,重合,则以(),,,为顶点的四面体的体积为______.
【难度】★★
【答案】
7.如图,与是四面体中互相垂直的棱,,若,且,其中,为常数,则四面体的体积的最大值是_____。
【难度】★★★
【答案】
8. 某几何体的三视图如图所示,且正视图、侧视图都是矩形,则该几何体的体积是( )
(A)16 (B)12 (C)8 (D)6
【难度】★★
【答案】B
9.若一个三棱锥的一条棱长为3,其余五条棱长都是2,那么这个三棱锥的体积等于________.
【难度】★★
【答案】
10.如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的主视图和左视图在下面画出(单位:cm).
(1)在主视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;
(三视图:主(正)试图、左(侧)视图、俯视图)
【难度】★★
【答案】 (1)如图.
(2)所求多面体的体积
V=V长方体-V正三棱锥=
多面体表面积的计算主要是运用空间中的直线与平面的基本知识与方法,计算出需要的几何量,然后根据平面几何的面积公式加以计算.
多面体体积的计算是多面体计算的重难点.直接计算多面体体积主要是计算出多面体的高,而这需要运用直线与平面垂直的方法技巧.对于复杂的几何体,要注意”割”与”补” 等方法的应用,注意改变几何体的观察角度,得到最佳求积方法, 注意等积变形的应用.
正四面体的性质 设正四面体的棱长为a,则这个正四面体的
(1)全面积 S全=a2; (2)体积 V=a3;
(3)对棱中点连线段的长 d=a; (4)相邻两面所成的二面角 α=arccos
(5)外接球半径 R=a; (6)内切球半径 r=a.
(7)正四面体内任意一点到四个面的距离之和为定值(等于正四面体的高).
1.正方体的对角线长为,则它的面的对角线长为_____.
【难度】★
【答案】
2.正六棱柱高5,最长的对角线为13,则它的侧面积是 .
【难度】★
【答案】180
3.正三棱锥的侧棱互相垂直,高为,则其体积等于________________.
【难度】★★
【答案】
4.斜三棱柱的底面是正三角形,侧棱和棱所成的角都是,若,则此三棱锥的侧面积为________________.
【难度】★★
【答案】
5.棱锥的底面是面积为9的矩形,它有两个侧面都垂直于底面,另外两个侧面分别与底面成角和角,此棱锥的体积为_______________;侧面积为________________.
【难度】★★
【答案】9;
6.在长方体中,已知顶点处的三条棱长分别为和2,求对角线与过的三个相邻面所成角的余弦的平方和.
【难度】★★
【答案】2
7.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60,求四棱锥P-ABCD的体积?
【难度】★★
【答案】2
【解析】在四棱锥P-ABCD中,由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成的角,∠PBO=60°。
在Rt△AOB中BO=ABsin30°=1, 由PO⊥BO,
于是PO=BOtan60°=,而底面菱形的面积为2。
∴四棱锥P-ABCD的体积V=×2×=2。
8.如图,一石柱的顶上是一个正四棱锥,下部是一个正四棱柱.已知正四棱柱的底面边长为0.5米,高1米,正四棱锥的高是0.3米,且石料的比重为每立方米重2400千克,求这个石柱的重量.
【难度】★★
【答案】660
9.在三棱锥S—ABC中,∠SAB=∠SAC=∠ACB=90°,且AC=BC=5,SB=5。(如图所示)
(Ⅰ)证明:SC⊥BC;
(Ⅱ)求侧面SBC与底面ABC所成二面角的大小;
(Ⅲ)求三棱锥的体积VS-ABC.
【难度】★★
【答案】60°,
【解析】(Ⅰ)证明:∵∠SAB=∠SAC=90°,
∴SA⊥AB,SA⊥AC。
又AB∩AC=A,
∴SA⊥平面ABC。
由于∠ACB=90°,即BC⊥AC,由三垂线定理,得SC⊥BC。
(Ⅱ)解:∵BC⊥AC,SC⊥BC。
∴∠SCA是侧面SCB与底面ABC所成二面角的平面角。
在Rt△SCB中,BC=5,SB=5,得SC==10。
在Rt△SAC中AC=5,SC=10,cosSCA=,
∴∠SCA=60°,即侧面SBC与底面ABC所成的二面角的大小为60°。
(Ⅲ)解:在Rt△SAC中,
∵SA=,
S△ABC=·AC·BC=×5×5=,
∴VS-ABC=·S△ACB·SA=。
如图,已知四面体ABCD中,,其余棱长均为2,则四面体的体积为 ,最大值为 。
【难度】★★
【答案】;
三棱锥P-ABC的侧棱PA、PB、PC两两互相垂直,侧面面积分别是6、4、3,则三棱锥的体积是 ( )
A、4 B、6 C、8 D、10
【难度】★★
【答案】A
正四棱锥的侧棱长是,底面边长都是,则它的全面积等于 ,体积等于 。
【难度】★★
【答案】;
正三棱锥的侧棱互相垂直,高为,则其体积等于________________.
【难度】★★
【答案】
斜三棱柱的底面是正三角形,侧棱和棱所成的角都是,若,则此三棱锥的侧面积为________________.
【难度】★★
【答案】
若一个三棱锥的一条棱长为3,其余五条棱长都是2,那么这个三棱锥的体积等于________.
【难度】★★
【答案】
棱锥的底面是面积为9的矩形,它有两个侧面都垂直于底面,另外两个侧面分别与底面成角和角,此棱锥的体积为_______________;侧面积为________________.
【难度】★★
【答案】9;
如图所示,三棱锥A—BCD一条侧棱AD=8 cm,底面一边BC=18 cm,其余四条棱的棱长都是17 cm,求三棱锥A—BCD的体积.
【难度】★★
【答案】取BC中点M,连接AM、DM,取AD的中点N,连接MN
∵AC=AB=CD=BD,∴BC⊥AM,BC⊥DM,
又∵AM∩DM=M,∴BC⊥平面ADM,BC=18,AC=AB=DB=DC=17.
∴AM=DM=4,∴NM⊥AD,∴MN=8.∴S△ADM=·MN·AD=·8·8=32.
∴VA—BCD=VB—ADM+VC—ADM=×S△ADM×(BM+CM)=×32×18=192(cm3).
三棱锥S—ABC中,一条棱长为a,其余棱长均为1,求a为何值时VS—ABC最大,并求最大值.
【难度】★★
【答案】如图所示,
设SC=a,其余棱长均为1,取AB的中点H,连接HS、HC,
则AB⊥HC,AB⊥HS,∴AB⊥平面SHC.
在面SHC中,过S作SO⊥HC,则SO⊥平面ABC.
在△SAB中,SA=AB=BS=1,∴SH=,
设∠SHO=,则SO=SHsin=sin,
∴VS—ABC=S△ABC·SO=××12×sin=sin≤.
当且仅当sin=1,即=90°时,三棱锥的体积最大.
a=SH=×=,Vmax=.
∴a为时,三棱锥的体积最大为.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,左视图(或称侧视图)是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V; (2)求该几何体的侧面积S.
【难度】★★
【答案】(1)由该几何体的俯视图、正视图、左视图可知,该几何体是四棱锥,且四棱锥的底面ABCD是边长为6和8的矩形,高VO=4,O点是AC与BD的交点.
∴该几何体的体积
V=×8×6×4=64.
(2)如图所示,侧面VAB中,VE⊥AB,则VE===5
∴S△VAB=×AB×VE=×8×5=20
侧面VBC中,VF⊥BC,
则VF===4.
∴S△VBC=×BC×VF=×6×4=12
∴该几何体的侧面积
S=2(S△VAB+S△VBC)=40+24.
如图所示,长方体ABCD—A′B′C′D′中,用截面截下一个棱锥C—A′DD′,求棱锥C—A′DD′的体积与剩余部分的体积之比.
【难度】★★
【答案】已知长方体可以看成直四棱柱ADD′A′—BCC′B′.
设它的底面ADD′A′面积为S,高为h,则它的体积为V=Sh.
而棱锥C—A′DD′的底面面积为S,高是h,
因此,棱锥C—A′DD′的体积
VC—A′DD′=×Sh=Sh.
余下的体积是Sh-Sh=Sh.
所以棱锥C—A′DD′的体积与剩余部分的体积之比为1∶5.
故这个三棱柱的表面积为(48+8)cm2,体积为16cm3.
已知三棱柱的底面为直角三角形,两条直角边和的长分别为4和3,侧棱的长为10.
(1)若侧棱垂直于底面,求该三棱柱的表面积.
(2)若侧棱与底面所成的角为,求该三棱柱的体积.
【难度】★★
【答案】(1)因为侧棱底面,所以三棱柱的高等于侧棱的长,
而底面三角形的面积,(2分)
周长,(4分)
于是三棱柱的表面积.(6分)
(2)如图,过作平面的垂线,垂足为,为三棱柱的高.(8分)
因为侧棱与底面所成的角为,所以,可计算得.(9分)
又底面三角形的面积,故三棱柱的体积.
在直三棱柱中,,,且异面直线与所成的角等于,设.求的值和三棱锥的体积.
【难度】★★
【答案】,
就是异面直线与所成的角,
即, ,连接,
则三棱锥的体积等于三棱锥的体积,
的面积, 又平面,
所以,所以.
另解:由于顶点到平面的距离与顶点到平面的距离相等
所以.
平面外的一点,两两互相垂直,过的中点作面,且,,,连,多面体的体积是.
(1)画出面与面的交线,说明理由;
(2)求与面所成的线面角的大小.
【难度】★★
【答案】(1)根据条件知:与交点恰好是
面,面, 面,面
面与面的交线
(2)两两互相垂直,面
多面体的体积是
连接,是在面的射影
是与面所成的线面角.
计算,
是与面所成的线面角 .
多面体的表面积和体积
知识梳理
例题解析
A
B
C
V
A
B
C
P
A
B
C
A1
B1
C1
B1
C1
C
B
D
A1
D1
A
E
F
A
B
C
D
P
C
A
B
P
①
②
反思总结
课后练习
图
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
