苏教版高二数学选修2-2:3.2复数的四则运算(乘方、除法)(共21张PPT)
文档属性
| 名称 | 苏教版高二数学选修2-2:3.2复数的四则运算(乘方、除法)(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 812.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 21:09:01 | ||
图片预览






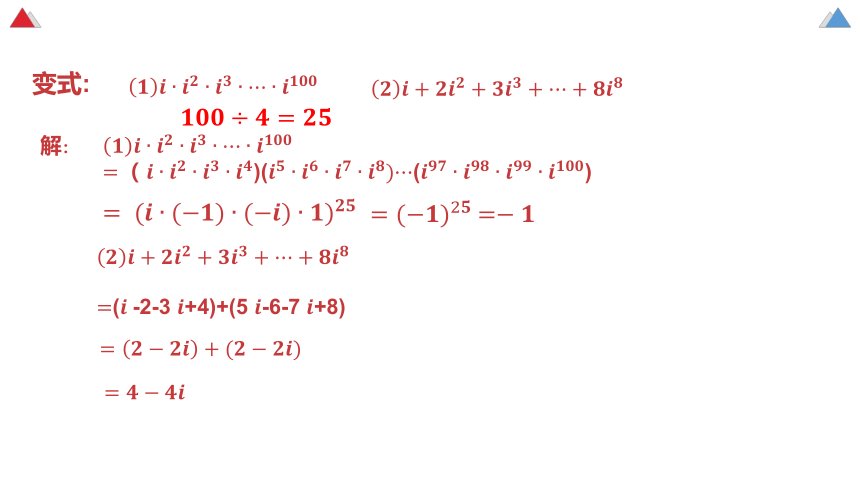


文档简介
(共21张PPT)
复数的四则运算(2)(乘方、除法)
江苏省江都中学
复习回顾
1、复数的加减法运算法则
2、复数乘法的法则
3、共轭复数
复数 z=a+bi 的共轭复数记作
共轭复数的简单性质:
实数
概念引入
一、复数的乘方
实数集R中正整数指数幂的运算律,在复数集C中仍然成立.即对任意的z,z1,z2∈C及m,n∈N*,有:
概念引入
【探究】 的指数变化规律
你能发现规律吗?有怎样的规律?
典型例题
【例1】 计算
(1+ )2= ___; (1- )2= ___;
2i
-2i
;
;
典型例题
【例2】求值:
+
:原式=( + +( + + + )+ +
( + + + )+ ( + + )=0++ = -1- =-1
方法优化:原式=( + (+ + + )+ +
( + + + )+( + + + )
=+ +0= -1- =-1
哪个方法简单?
变式:
解:
( )(()
(-2-3 +4)+(5 -6-7 +8)
典型例题
【例3】设
求证:
⑴
证明:
(2)
=() ( )=+=1
题后反思:
如果把例3中的 换成 ,那么欲证的两个等式还成立吗?在复数范围内,你能写出方程 的3个根吗?
答:成立,方程的3个根分别是:
=1+ +=0
上例知 , 1,得= =
=
概念引入
二、复数的除法
在实数中,除法运算是乘法的逆运算,
类似地,可以定义复数的除法运算:
定义: 把满足(c+di)(x+yi) =a+bi (c+di≠0) 的复 数 x+yi 叫做复数 a+bi 除以复数 c+di 的商, (其中a,b,c,d,x,y都是实数)
记为:
探究结论
复数的除法是不是等于对应实部和虚部相除呢?先看一个例子:
?
:()()=1 2+() = 1
结论:两个复数的除法对应的复数的实部不等于对应实部相除,虚部不等于对应虚部相除。
思考:复数的除法究竟怎么算?
探究结论
探究结论
另解:
探究结论
计算:
比较两个方法,哪个更好?
点评:法一是待定系数法,法二是利用初中我们学习的化简
无理分式时,采用的分母有理化的思想方法,复数
,相当于初中学习的对偶式
,它们之积为1是有理数,叫分母有理化,而
( )( )=25是正实数,所以可以使分母为实
数,把这种方法叫分母实数化。
构建新知
复数的除法法则
一般地,我们有:
由于 所以 ,可见,两个复数的商仍是一个确定的复数。
分子分母同乘以分母的共轭复数,
即把分母 “实数化”。
)
典型例题
==
【例4】计算:
1):
变式训练
1)
: =(
计算: (1)
==-4
变式训练
计算: (2)
=
=
点评:跟实数一样,加减是最低级运算,乘方是最高级
运算。有括号先算括号,没有括号,先算乘方,其次乘
除,最后算加减。
常用结论:
(1)
(2)
(3)
(4)
课堂小结
2、除法运算法则
本质:分母实数化
1、i的乘方
思考题:
计算:
解:原式=
复数的四则运算(2)(乘方、除法)
江苏省江都中学
复习回顾
1、复数的加减法运算法则
2、复数乘法的法则
3、共轭复数
复数 z=a+bi 的共轭复数记作
共轭复数的简单性质:
实数
概念引入
一、复数的乘方
实数集R中正整数指数幂的运算律,在复数集C中仍然成立.即对任意的z,z1,z2∈C及m,n∈N*,有:
概念引入
【探究】 的指数变化规律
你能发现规律吗?有怎样的规律?
典型例题
【例1】 计算
(1+ )2= ___; (1- )2= ___;
2i
-2i
;
;
典型例题
【例2】求值:
+
:原式=( + +( + + + )+ +
( + + + )+ ( + + )=0++ = -1- =-1
方法优化:原式=( + (+ + + )+ +
( + + + )+( + + + )
=+ +0= -1- =-1
哪个方法简单?
变式:
解:
( )(()
(-2-3 +4)+(5 -6-7 +8)
典型例题
【例3】设
求证:
⑴
证明:
(2)
=() ( )=+=1
题后反思:
如果把例3中的 换成 ,那么欲证的两个等式还成立吗?在复数范围内,你能写出方程 的3个根吗?
答:成立,方程的3个根分别是:
=1+ +=0
上例知 , 1,得= =
=
概念引入
二、复数的除法
在实数中,除法运算是乘法的逆运算,
类似地,可以定义复数的除法运算:
定义: 把满足(c+di)(x+yi) =a+bi (c+di≠0) 的复 数 x+yi 叫做复数 a+bi 除以复数 c+di 的商, (其中a,b,c,d,x,y都是实数)
记为:
探究结论
复数的除法是不是等于对应实部和虚部相除呢?先看一个例子:
?
:()()=1 2+() = 1
结论:两个复数的除法对应的复数的实部不等于对应实部相除,虚部不等于对应虚部相除。
思考:复数的除法究竟怎么算?
探究结论
探究结论
另解:
探究结论
计算:
比较两个方法,哪个更好?
点评:法一是待定系数法,法二是利用初中我们学习的化简
无理分式时,采用的分母有理化的思想方法,复数
,相当于初中学习的对偶式
,它们之积为1是有理数,叫分母有理化,而
( )( )=25是正实数,所以可以使分母为实
数,把这种方法叫分母实数化。
构建新知
复数的除法法则
一般地,我们有:
由于 所以 ,可见,两个复数的商仍是一个确定的复数。
分子分母同乘以分母的共轭复数,
即把分母 “实数化”。
)
典型例题
==
【例4】计算:
1):
变式训练
1)
: =(
计算: (1)
==-4
变式训练
计算: (2)
=
=
点评:跟实数一样,加减是最低级运算,乘方是最高级
运算。有括号先算括号,没有括号,先算乘方,其次乘
除,最后算加减。
常用结论:
(1)
(2)
(3)
(4)
课堂小结
2、除法运算法则
本质:分母实数化
1、i的乘方
思考题:
计算:
解:原式=
