沪教版数学高二下春季班:第十讲球的体积及球面距离 同步学案(教师版)
文档属性
| 名称 | 沪教版数学高二下春季班:第十讲球的体积及球面距离 同步学案(教师版) | 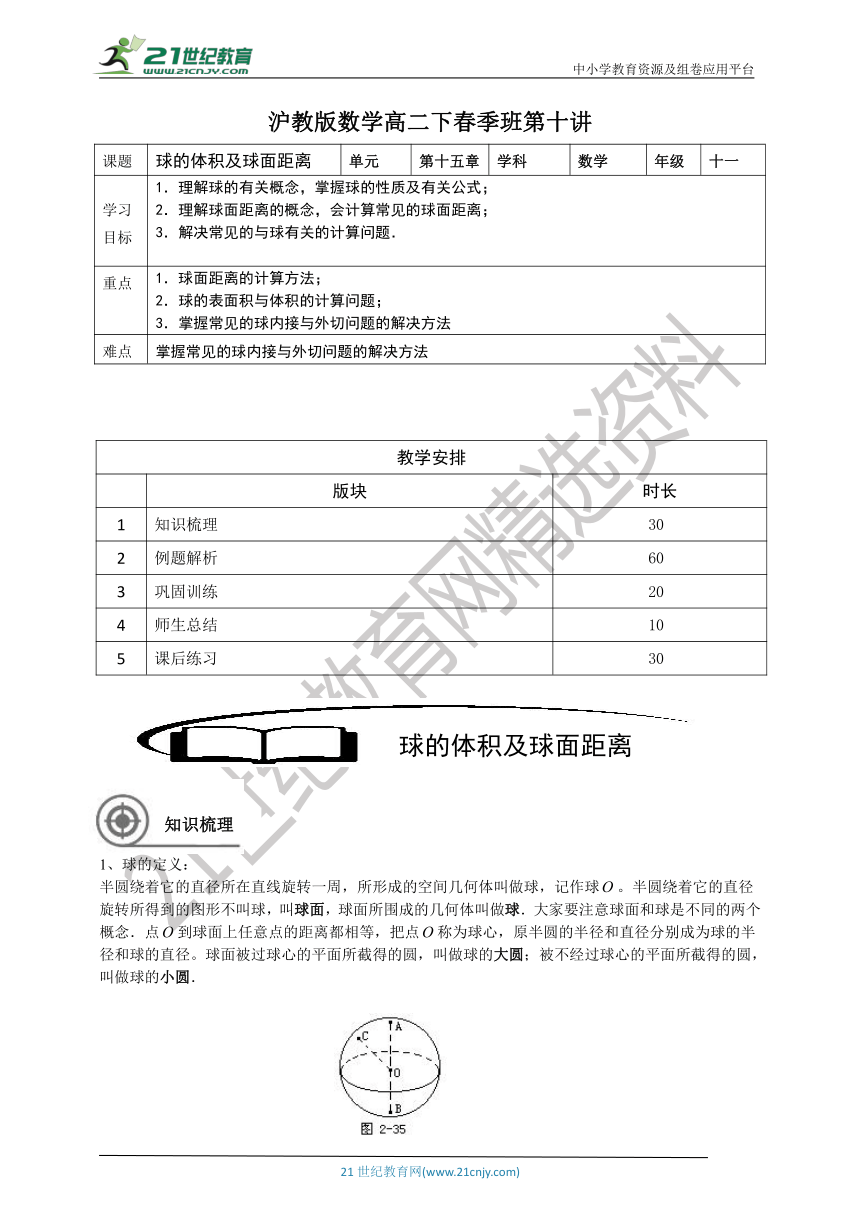 | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 11:33:56 | ||
图片预览





文档简介
沪教版数学高二下春季班第十讲
课题
球的体积及球面距离
单元
第十五章
学科
数学
年级
十一
学习
目标
1.理解球的有关概念,掌握球的性质及有关公式;
2.理解球面距离的概念,会计算常见的球面距离;
3.解决常见的与球有关的计算问题.
重点
1.球面距离的计算方法;
2.球的表面积与体积的计算问题;
3.掌握常见的球内接与外切问题的解决方法
难点
掌握常见的球内接与外切问题的解决方法
教学安排
版块
时长
1
知识梳理
30
2
例题解析
60
3
巩固训练
20
4
师生总结
10
5
课后练习
30
1、球的定义:
半圆绕着它的直径所在直线旋转一周,所形成的空间几何体叫做球,记作球。半圆绕着它的直径旋转所得到的图形不叫球,叫球面,球面所围成的几何体叫做球.大家要注意球面和球是不同的两个概念.点到球面上任意点的距离都相等,把点称为球心,原半圆的半径和直径分别成为球的半径和球的直径。球面被过球心的平面所截得的圆,叫做球的大圆;被不经过球心的平面所截得的圆,叫做球的小圆.
2、球的性质:
球心和截面圆心的连线垂直于截面;设球心到截面的距离为d,截面圆的半径为r,球的半径为R,则:r=
圆的主要性质
球的主要性质
1
平面内与定点距离等于定长的点集
(轨迹)
空间与定点距离等于定长的点集(轨迹)是球面
2
同圆(或等圆)的半径相等,直径是半径的2倍
同球(或等球)的半径相等,直径是半径的2倍
3
与弦垂直的直径过弦的中点,圆半径2=圆心到弦距离2+弦长的一半2
与截面积垂直的直径过截面圆的圆心,球半径2=球心到截面圆距离2+截面圆的半径2
4
不过圆心的弦小于直径;经过圆心的弦是直径,是最大的弦
不过球心的截得的是球的小圆,其半径和面积都小于球的大圆的半径和面积;经过球心的截面截得的是球的大圆,是最大的截面圆
5
过切点的圆半径垂直于圆的切线
过切点的球半径垂直于球的切面
6
圆周长=2π×圆半径
大圆周长=2π×球半径
3、球的表面积、体积公式:表面积:;球的体积公式:.
4、球的体积公式
高中数学教材对球的体积公式(为球的半径)作了要求,但只是简单地说“利用祖暅原理和圆柱、圆锥的体积公式”可得出此公式,未作具体推导.
鉴于部分学有余力的学生想了解其推导过程,现提供几种用高中数学知识就可推导的方法.
方法一:利用祖暅原理
为方便起见,现只计算半球的体积.正如教材中所说的方法,利用祖暅原理关键是要构造一个和半球等高且横截面面积处处相等的几何体.
如图1,
在一个底面半径为、高为的圆柱中挖去一个底面半径为、高为的圆锥,
则距离下底面的横截面为一圆环,面积为.
又半球距离下底面的横截面为一个圆,由勾股定理,半径为,面积也为.
因此,所构造几何体的体积与半球的体积相等,为圆柱的体积减去圆锥的体积,
即,
所以球的体积为.
方法二:把球分割成无穷多个小圆柱
高中生已经学过极限的知识,可以尝试这个方法.同样,只计算半球的体积. 如图2,
把半球的高等分,作个半球的横截面,再以这些横截面为底面,作个高为的圆柱.这些圆柱的底面积分别为,,,所以这些圆柱的体积之和是
当时,圆柱体积之和就无限趋近于半球的体积,即,所以球的体积为.
方法三、把球分割成无穷多个小圆锥
把球面近似分成个部分,当时,每个部分可看做一个圆.以这些圆为底面,以球心为顶点做圆锥,则所有圆锥体积的和即为球的体积.
如图3.
设每个圆的面积为,则所有圆锥体积的和为
又球的表面积为,所以球的体积为.
这种推导方法比较简单易懂,但需要用到球的表面积公式,而他无法用高中数学知识推导,顾此方法的说服力不如前两种方法.
4、经度、纬度:
经线:球面上从北极到南极的半个大圆
纬线:与赤道平面平行的平面截球面所得的小圆
经度:某地的经度就是经过这点的经线与地轴确定的半平面与经线及轴确定的半平面所成的二面角的度数
纬度:某地的纬度就是指过这点的球半径与赤道平面所成角的度数
5、球面距离:球面上两点之间的最短距离,也是过两点的大圆的圆弧(劣弧)长度.
(1)两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离 即: (为球心角的弧度数).
(2)半球的底面: 已知半径为的球,用过球心的平面去截球,球被截面分成大小相等的两个半球,截面圆(包含它内部的点),叫做所得半球的底面.
1、球的概念与球的截面
【例1】① 当平面到球心的距离小于球半径时,球面与平面的交线总是一个圆;
② 过球面上两点只能作一个球大圆; ③ 过空间四点总能作一个球;
④ 球的任意两个大圆的交点的连线是球的直径.以上四个命题中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
【难度】★
【答案】C
【例2】已知半径为的球的两个平行截面的周长分别为和,则两平行截面间的距离为( )
A. B. C.或 D.或
【难度】★
【答案】C
【例3】棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积。
【难度】★★
【答案】如图,为题中的三角形,
由已知得,,,,
∴的面积为
【例4】已知正三个顶点都在半径为2的球面上,球心到平面的距离为1,点是线段的中点,过点作球的截面,则截面面积的最小值是________.
【难度】★★
【答案】
【巩固训练】
1.判断正误
(1)过球的一条直径的大圆有无数个;( )
(2)过球面上三点的大圆仅有一个;( )
(3)球面上两点间的直线段距离叫做两点的球面距离;( )
(4)通过球面上两点的大圆劣弧长叫做两点的球面距离;( )
(5)两点的球面距离是球面上连接两点的最短路径;( )
(6)两点在半径为的球面上,为球心,若,则两点的球面距离为. ( )
【难度】★
【答案】1.√ 2.╳ 3.╳ 4.√ 5.√ 6.╳
2.已知球的表面积为,有两个平行截面的面积分别为、,则这两个平行截面间的距离为 。
【难度】★★【答案】9或39
3.过球表面上一点引三条长度相等的弦、、,且两两夹角都为,若球半径为,求弦的长度.
【难度】★★
【答案】由条件可抓住是正四面体,、、、为球上四点,则球心在正四面体中心,设,则截面与球心的距离,过点、、的截面圆半径,所以得.
4.如图,AB是球O的直径,C、D是球面上两点,且点D在以BC为直径的小圆上,设小圆所在的平面为. (1)求证:平面ABC ; (2)设D为BC弧的中点,AD与平面 所成角为 ,过球的半径OD且垂直于截面BC弦于点E,求△OED与过OD的截面圆的面积之比.
【难度】★★
【答案】
【解析】(1)取BC的中点O1,连OO1,因为O1是以BC为直径的圆的圆心,
则OO1⊥BC,D为圆周上的一点。
(2)因为⊿BOC,⊿ABC都是等腰三角形,取BC的中点M,连OM,AM,过O作OH⊥AM,可证得OH⊥面ABC即OH是O到截面ABC的距离。 (另:利用等体积法也可求得)
2、经纬度与球面距离
【例5】球面上有3个点,其中任意两点的球面距离都等于大圆周长的,经过3个点的小圆的周长为,求这个球的半径.
【难度】★
【答案】设球的半径为,小圆的半径为,则,∴.
如图所示,设三点、、,为球心,.
又∵,∴是等边三角形,同样,、都是等边三角形,
得为等边三角形,边长等于球半径.为的外接圆半径,,.
【例6】设地球半径为,在北纬圈上有,两地,它们在纬度圈上的弧长等于,求,两地间的球面距离.
【难度】★
【答案】如图所示,是北纬圈上的两点,为它的半径,
∴⊥,⊥∵==,
∴;则==;
∴=;∴= =.
在中, 则为正三角形,∴;
∴两点间的球面距离为
【例7】在地球本初子午线上有两点。它们的纬度差为,若地球半径为,求两点间的球面距离。
【难度】★
【答案】如图所示,设为地球球心,由题意可得故。
【例8】设地球上两点,,其中位于北纬,位于南纬,且、两点的经度差为,求、两点的球面距离。
【难度】★★
【答案】如图所示,设,分别为地球球心、
北纬纬线圈的圆心和南纬纬线圈的圆心。
连结
,,则由异面直线上两点间的距离公式得
即两点的球面距离为
【巩固训练】
1.若地球半径为R,在北纬45°圈上有A、B两点,且这两点间的球面距离为,则北
纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为
【难度】★【答案】
2.在地球北纬度圈上有两点,它们的经度差为度,若地球半径为,求两点间的球面距离。
【难度】★
【答案】设度的纬线圈的圆心为,半径为,则。依题意。取的中点,则。
3.地球半径为,地位于经度,北纬;地位于纬度,东经。
(1)地球自转6小时,地旋转了多少路程?
(2)求两地的球面距离.
【难度】★★
【答案】;
【解析】设纬度的大圆圆心为,北纬的小圆圆心为。两地的位置如图所示。
(1)易知,地球自转6小时,
地在北纬的小圆圆周上旋转的圆心角为,则它所经过的路程为。
(2)可看作异面直线与上的两点,是异面直线与的公垂线段。
过作大圆的垂线,垂足为,则
,
∴,则,故求两地的球面距离为。
4.地球上两地分别在北纬和的纬度圈上,且经度差为,设为地球半径,求 两地之间的球面距离.
【难度】★★
【答案】两地之间的球面距离为。
3、球的表面积与体积
【例9】长方体的一个顶点上三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是 ( )
A20π B25π C50π D200π
【难度】★【答案】C
【解析】设球的半径为R,则(2R)2=32+42+52=50,∴R=∴S球=4π×R2=50π
【例10】已知球的半径为R,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
【答案】下图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
则()2+r2=R2,
即h=2
∵S=2πrh=4πr·=4π
≤4π=2πR2,
取等号时,内接圆柱底面半径为R,高为R
【例11】点在同一个球的球面上,,若四面体体积的最大值为,则这个球的表面积为( )
A. B. C. D.
【难度】★★
【答案】
【解析】如图所示,为球的球心,由可知,即所在的小圆的圆心1为的中点,故,当为的延长线与球面的交点时,到平面的距离最大,四面体的体积最大.连接,设球的半径为,则,此时,解得,故这个球的表面积为=.
【例12】已知三棱锥内接于球,三条侧棱两两垂直且长都等于1,求球的表面积和体积.
【难度】★★★
【答案】
【解析】设的中心为,则三点共线,设直线交球面于,连接。
因为三条侧棱两两垂直且长都等于1,所以,
从而,。
易知是直角斜边上的高。
由射影定理,,即。
设球的半径为,则。所以,。
【巩固训练】
1.如果球的大圆的面积增大为原来的倍,那么球的体积增大为原来的 ( )
A.倍 B.倍 C.倍 D.倍
【难度】★
【答案】B
2.64个直径都为的球,记它们的体积之和为,表面积之和为;一个直径为的球,记其体积为,表面积为,则( ) A. B. C. D. 【难度】★★
【答案】C
3.如果球、正方体与等边圆柱(底面直径与母线相等)的体积相等,求它们的表面积的大小关系.
【难度】★★
【答案】设球的半径为R、正方体的棱长为a , 等边圆柱的底面半径为r, 且它们的体积都为V,
则:, .
, .
4.设是球面上的四个点,且在同一平面内,,球心到该平面的距离是球半径的一半,求这个球的体积.
【难度】★★
【答案】
【解析】 因是球面上的四个点,且在同一平面内,因而,
。
4、球的内接和外切问题
【例13】已知正方体的棱长为2,它的八个顶点都在某个球面上,则两点的球面距离是__________.
【难度】★★【答案】
【例14】正三棱锥内有一个内切球,经过棱锥的一条侧棱和高作截面,正确的图是 ( )
A B C D
【难度】★★
【答案】C
【例15】A、B、C是半径为1的球面上三点,B、C间的球面距离为,点A与B、C两点间的球面距离均为,且球心为O,求:
(1)∠AOB,∠BOC的大小;
(2)球心到截面ABC的距离;
(3)球的内接正方体的表面积与球面积之比.
【难度】★★★
【答案】(1)∠AOB=,∠BOC=;(2)d=;(3)2∶.
【例16】如图,在斜三棱柱中, ,侧面与底面ABC所成的二面角为,E、F分别是棱的中点.
(1)求与底面ABC所成的角;
(2)证明∥平面;
(3)求经过四点的球的体积.
【难度】★★★
【答案】(1)60°;(2)略;(3)
【巩固训练】
1.一个四面体的所有棱长都为, 四个顶点在同一球面上, 则此球的表面积是 ( )
A.3π B.4π C.3π D.6π
【难度】★★
【答案】A
2.半径为的球内切于一个圆锥,求该圆锥体积的最小值.
【难度】★
【答案】
【解析】如图,设该圆锥底面半径为,高为,并设球心切母线于。则∽。
∴,即,∴。
令,则,当且仅当时,等号成立。
故,此时。
3.将半径为R的五个球中的四个放在桌面上,使每相邻两个球相切,第五个球放在四个球上,使它与这四个球都相切,则这第五个球球心到桌面的距离为 .
【难度】★★
【答案】
4.球面上三点组成这个球的一个截面的内接三角形,,且球心到该截面的距离为球的半径的一半,
(1)求球的体积; (2)求两点的球面距离.
【难度】★★
【答案】;
球面距离的计算需要先搞清楚经度、纬度、大圆、小圆等概念,然后计算过两点的大圆的圆弧(劣弧)长度。常见的有同赤道,同经度、同纬度几种,经度纬度都不同的情况较难,但是原理是相同的.
计算球的表面积和体积主要利用前面所学的立体几何知识,求出球的半径,然后使用相应公式计算即可.
在球的有关问题中,常见球内接几何体或者球外切几何体的问题.球内接几何体的问题中,球内接棱柱的体对角线为球的直径,这是解决这一类问题的关键点;球外切几何体的问题,一般与球的直径垂直于面相关.
1.面半径2R的圆柱形铁罐做一种半径为R的球型产品的外包装,一听4个,铁罐的高度至少应为 .
【难度】★★
【答案】2R
2.圆柱形容器内盛有高度为的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________
【难度】★★
【答案】
【解析】设球的半径为,则.解得.
3.圆锥的高为,侧面积为,其内切球的表面积为________.
【难度】★★
【答案】
【解析】设圆锥底面半径为,则母线长,由得,解之得,∴.设内切球半径为,作出圆锥的轴截面如图,则,,,,
∴球的表面积.
4.半径为的球内部装有个半径相同的小球,则小球半径的可能最大值为(??).
A. B. B. D.
【难度】★★
【答案】
5.已知三棱锥的所有顶点都在球的球面上,是边长为的正三角形,为球的直径,且,则此棱锥的体积为( )
A. B. C. D.
【难度】★★
【答案】A
【解析】如图,为的外接圆圆心,则,设的外接圆半径为,
则,
∴.连接,根据球的截面性质知,
,为的中点,∴到平面的距离为,∴
6.点在同一个球的球面上,,若四面体体积的最大值为,则这个球的表面积为( )
A. B. C. D.
【难度】★★
【答案】
【解析】如图所示,为球的球心,由可知,即所在的小圆的圆心1为的中点,故,当为的延长线与球面的交点时,到平面的距离最大,四面体的体积最大.连接,设球的半径为,则,此时,解得,故这个球的表面积为=.
7.若一个正四面体的表面积为,其内切球的表面积为,则=________.
【难度】★★
【答案】
【解析】设正四面体棱长为,则正四面体表面积为,其内切球半径为正四面体高的,即,因此内切球表面积为,则.
8.如图,直三棱柱的六个顶点都在半径为的半球面上,,侧面是半球底面圆的内接正方形,则侧面的面积为( )
【难度】★★
【答案】
【解析】由题意知,球心在侧面的中心上,为截面圆的直径,∴,的外接圆圆心是的中点,同理的外心是的中心.设正方形的边长为,中,(为球的半径),∴,即,则,∴矩形.
9.一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为的正方形),则该几何体外接球的体积为________.
【难度】★★
【答案】
【解析】依题意可知,新的几何体的外接球也就是原正方体的外接球,要求的直径就是正方体的体对角线;∴(为球的半径),∴,∴球的体积.
10.正四棱锥的顶点都在同一球面上,若该棱锥的高为,底面边长为,则该球的表面积为( )
【难度】★★
【答案】
【解析】如图所示,设球半径为,底面中心为且球心为,∵正四棱锥中∵,∴在中,,∴,解得,∴该球的表面积为,故选.
课题
球的体积及球面距离
单元
第十五章
学科
数学
年级
十一
学习
目标
1.理解球的有关概念,掌握球的性质及有关公式;
2.理解球面距离的概念,会计算常见的球面距离;
3.解决常见的与球有关的计算问题.
重点
1.球面距离的计算方法;
2.球的表面积与体积的计算问题;
3.掌握常见的球内接与外切问题的解决方法
难点
掌握常见的球内接与外切问题的解决方法
教学安排
版块
时长
1
知识梳理
30
2
例题解析
60
3
巩固训练
20
4
师生总结
10
5
课后练习
30
1、球的定义:
半圆绕着它的直径所在直线旋转一周,所形成的空间几何体叫做球,记作球。半圆绕着它的直径旋转所得到的图形不叫球,叫球面,球面所围成的几何体叫做球.大家要注意球面和球是不同的两个概念.点到球面上任意点的距离都相等,把点称为球心,原半圆的半径和直径分别成为球的半径和球的直径。球面被过球心的平面所截得的圆,叫做球的大圆;被不经过球心的平面所截得的圆,叫做球的小圆.
2、球的性质:
球心和截面圆心的连线垂直于截面;设球心到截面的距离为d,截面圆的半径为r,球的半径为R,则:r=
圆的主要性质
球的主要性质
1
平面内与定点距离等于定长的点集
(轨迹)
空间与定点距离等于定长的点集(轨迹)是球面
2
同圆(或等圆)的半径相等,直径是半径的2倍
同球(或等球)的半径相等,直径是半径的2倍
3
与弦垂直的直径过弦的中点,圆半径2=圆心到弦距离2+弦长的一半2
与截面积垂直的直径过截面圆的圆心,球半径2=球心到截面圆距离2+截面圆的半径2
4
不过圆心的弦小于直径;经过圆心的弦是直径,是最大的弦
不过球心的截得的是球的小圆,其半径和面积都小于球的大圆的半径和面积;经过球心的截面截得的是球的大圆,是最大的截面圆
5
过切点的圆半径垂直于圆的切线
过切点的球半径垂直于球的切面
6
圆周长=2π×圆半径
大圆周长=2π×球半径
3、球的表面积、体积公式:表面积:;球的体积公式:.
4、球的体积公式
高中数学教材对球的体积公式(为球的半径)作了要求,但只是简单地说“利用祖暅原理和圆柱、圆锥的体积公式”可得出此公式,未作具体推导.
鉴于部分学有余力的学生想了解其推导过程,现提供几种用高中数学知识就可推导的方法.
方法一:利用祖暅原理
为方便起见,现只计算半球的体积.正如教材中所说的方法,利用祖暅原理关键是要构造一个和半球等高且横截面面积处处相等的几何体.
如图1,
在一个底面半径为、高为的圆柱中挖去一个底面半径为、高为的圆锥,
则距离下底面的横截面为一圆环,面积为.
又半球距离下底面的横截面为一个圆,由勾股定理,半径为,面积也为.
因此,所构造几何体的体积与半球的体积相等,为圆柱的体积减去圆锥的体积,
即,
所以球的体积为.
方法二:把球分割成无穷多个小圆柱
高中生已经学过极限的知识,可以尝试这个方法.同样,只计算半球的体积. 如图2,
把半球的高等分,作个半球的横截面,再以这些横截面为底面,作个高为的圆柱.这些圆柱的底面积分别为,,,所以这些圆柱的体积之和是
当时,圆柱体积之和就无限趋近于半球的体积,即,所以球的体积为.
方法三、把球分割成无穷多个小圆锥
把球面近似分成个部分,当时,每个部分可看做一个圆.以这些圆为底面,以球心为顶点做圆锥,则所有圆锥体积的和即为球的体积.
如图3.
设每个圆的面积为,则所有圆锥体积的和为
又球的表面积为,所以球的体积为.
这种推导方法比较简单易懂,但需要用到球的表面积公式,而他无法用高中数学知识推导,顾此方法的说服力不如前两种方法.
4、经度、纬度:
经线:球面上从北极到南极的半个大圆
纬线:与赤道平面平行的平面截球面所得的小圆
经度:某地的经度就是经过这点的经线与地轴确定的半平面与经线及轴确定的半平面所成的二面角的度数
纬度:某地的纬度就是指过这点的球半径与赤道平面所成角的度数
5、球面距离:球面上两点之间的最短距离,也是过两点的大圆的圆弧(劣弧)长度.
(1)两点的球面距离:球面上两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离 即: (为球心角的弧度数).
(2)半球的底面: 已知半径为的球,用过球心的平面去截球,球被截面分成大小相等的两个半球,截面圆(包含它内部的点),叫做所得半球的底面.
1、球的概念与球的截面
【例1】① 当平面到球心的距离小于球半径时,球面与平面的交线总是一个圆;
② 过球面上两点只能作一个球大圆; ③ 过空间四点总能作一个球;
④ 球的任意两个大圆的交点的连线是球的直径.以上四个命题中正确的有 ( )
A.0个 B.1个 C.2个 D.3个
【难度】★
【答案】C
【例2】已知半径为的球的两个平行截面的周长分别为和,则两平行截面间的距离为( )
A. B. C.或 D.或
【难度】★
【答案】C
【例3】棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积。
【难度】★★
【答案】如图,为题中的三角形,
由已知得,,,,
∴的面积为
【例4】已知正三个顶点都在半径为2的球面上,球心到平面的距离为1,点是线段的中点,过点作球的截面,则截面面积的最小值是________.
【难度】★★
【答案】
【巩固训练】
1.判断正误
(1)过球的一条直径的大圆有无数个;( )
(2)过球面上三点的大圆仅有一个;( )
(3)球面上两点间的直线段距离叫做两点的球面距离;( )
(4)通过球面上两点的大圆劣弧长叫做两点的球面距离;( )
(5)两点的球面距离是球面上连接两点的最短路径;( )
(6)两点在半径为的球面上,为球心,若,则两点的球面距离为. ( )
【难度】★
【答案】1.√ 2.╳ 3.╳ 4.√ 5.√ 6.╳
2.已知球的表面积为,有两个平行截面的面积分别为、,则这两个平行截面间的距离为 。
【难度】★★【答案】9或39
3.过球表面上一点引三条长度相等的弦、、,且两两夹角都为,若球半径为,求弦的长度.
【难度】★★
【答案】由条件可抓住是正四面体,、、、为球上四点,则球心在正四面体中心,设,则截面与球心的距离,过点、、的截面圆半径,所以得.
4.如图,AB是球O的直径,C、D是球面上两点,且点D在以BC为直径的小圆上,设小圆所在的平面为. (1)求证:平面ABC ; (2)设D为BC弧的中点,AD与平面 所成角为 ,过球的半径OD且垂直于截面BC弦于点E,求△OED与过OD的截面圆的面积之比.
【难度】★★
【答案】
【解析】(1)取BC的中点O1,连OO1,因为O1是以BC为直径的圆的圆心,
则OO1⊥BC,D为圆周上的一点。
(2)因为⊿BOC,⊿ABC都是等腰三角形,取BC的中点M,连OM,AM,过O作OH⊥AM,可证得OH⊥面ABC即OH是O到截面ABC的距离。 (另:利用等体积法也可求得)
2、经纬度与球面距离
【例5】球面上有3个点,其中任意两点的球面距离都等于大圆周长的,经过3个点的小圆的周长为,求这个球的半径.
【难度】★
【答案】设球的半径为,小圆的半径为,则,∴.
如图所示,设三点、、,为球心,.
又∵,∴是等边三角形,同样,、都是等边三角形,
得为等边三角形,边长等于球半径.为的外接圆半径,,.
【例6】设地球半径为,在北纬圈上有,两地,它们在纬度圈上的弧长等于,求,两地间的球面距离.
【难度】★
【答案】如图所示,是北纬圈上的两点,为它的半径,
∴⊥,⊥∵==,
∴;则==;
∴=;∴= =.
在中, 则为正三角形,∴;
∴两点间的球面距离为
【例7】在地球本初子午线上有两点。它们的纬度差为,若地球半径为,求两点间的球面距离。
【难度】★
【答案】如图所示,设为地球球心,由题意可得故。
【例8】设地球上两点,,其中位于北纬,位于南纬,且、两点的经度差为,求、两点的球面距离。
【难度】★★
【答案】如图所示,设,分别为地球球心、
北纬纬线圈的圆心和南纬纬线圈的圆心。
连结
,,则由异面直线上两点间的距离公式得
即两点的球面距离为
【巩固训练】
1.若地球半径为R,在北纬45°圈上有A、B两点,且这两点间的球面距离为,则北
纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为
【难度】★【答案】
2.在地球北纬度圈上有两点,它们的经度差为度,若地球半径为,求两点间的球面距离。
【难度】★
【答案】设度的纬线圈的圆心为,半径为,则。依题意。取的中点,则。
3.地球半径为,地位于经度,北纬;地位于纬度,东经。
(1)地球自转6小时,地旋转了多少路程?
(2)求两地的球面距离.
【难度】★★
【答案】;
【解析】设纬度的大圆圆心为,北纬的小圆圆心为。两地的位置如图所示。
(1)易知,地球自转6小时,
地在北纬的小圆圆周上旋转的圆心角为,则它所经过的路程为。
(2)可看作异面直线与上的两点,是异面直线与的公垂线段。
过作大圆的垂线,垂足为,则
,
∴,则,故求两地的球面距离为。
4.地球上两地分别在北纬和的纬度圈上,且经度差为,设为地球半径,求 两地之间的球面距离.
【难度】★★
【答案】两地之间的球面距离为。
3、球的表面积与体积
【例9】长方体的一个顶点上三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是 ( )
A20π B25π C50π D200π
【难度】★【答案】C
【解析】设球的半径为R,则(2R)2=32+42+52=50,∴R=∴S球=4π×R2=50π
【例10】已知球的半径为R,在球内作一个内接圆柱,这个圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?
【答案】下图为轴截面,令圆柱的高为h,底面半径为r,侧面积为S,
则()2+r2=R2,
即h=2
∵S=2πrh=4πr·=4π
≤4π=2πR2,
取等号时,内接圆柱底面半径为R,高为R
【例11】点在同一个球的球面上,,若四面体体积的最大值为,则这个球的表面积为( )
A. B. C. D.
【难度】★★
【答案】
【解析】如图所示,为球的球心,由可知,即所在的小圆的圆心1为的中点,故,当为的延长线与球面的交点时,到平面的距离最大,四面体的体积最大.连接,设球的半径为,则,此时,解得,故这个球的表面积为=.
【例12】已知三棱锥内接于球,三条侧棱两两垂直且长都等于1,求球的表面积和体积.
【难度】★★★
【答案】
【解析】设的中心为,则三点共线,设直线交球面于,连接。
因为三条侧棱两两垂直且长都等于1,所以,
从而,。
易知是直角斜边上的高。
由射影定理,,即。
设球的半径为,则。所以,。
【巩固训练】
1.如果球的大圆的面积增大为原来的倍,那么球的体积增大为原来的 ( )
A.倍 B.倍 C.倍 D.倍
【难度】★
【答案】B
2.64个直径都为的球,记它们的体积之和为,表面积之和为;一个直径为的球,记其体积为,表面积为,则( ) A. B. C. D. 【难度】★★
【答案】C
3.如果球、正方体与等边圆柱(底面直径与母线相等)的体积相等,求它们的表面积的大小关系.
【难度】★★
【答案】设球的半径为R、正方体的棱长为a , 等边圆柱的底面半径为r, 且它们的体积都为V,
则:, .
, .
4.设是球面上的四个点,且在同一平面内,,球心到该平面的距离是球半径的一半,求这个球的体积.
【难度】★★
【答案】
【解析】 因是球面上的四个点,且在同一平面内,因而,
。
4、球的内接和外切问题
【例13】已知正方体的棱长为2,它的八个顶点都在某个球面上,则两点的球面距离是__________.
【难度】★★【答案】
【例14】正三棱锥内有一个内切球,经过棱锥的一条侧棱和高作截面,正确的图是 ( )
A B C D
【难度】★★
【答案】C
【例15】A、B、C是半径为1的球面上三点,B、C间的球面距离为,点A与B、C两点间的球面距离均为,且球心为O,求:
(1)∠AOB,∠BOC的大小;
(2)球心到截面ABC的距离;
(3)球的内接正方体的表面积与球面积之比.
【难度】★★★
【答案】(1)∠AOB=,∠BOC=;(2)d=;(3)2∶.
【例16】如图,在斜三棱柱中, ,侧面与底面ABC所成的二面角为,E、F分别是棱的中点.
(1)求与底面ABC所成的角;
(2)证明∥平面;
(3)求经过四点的球的体积.
【难度】★★★
【答案】(1)60°;(2)略;(3)
【巩固训练】
1.一个四面体的所有棱长都为, 四个顶点在同一球面上, 则此球的表面积是 ( )
A.3π B.4π C.3π D.6π
【难度】★★
【答案】A
2.半径为的球内切于一个圆锥,求该圆锥体积的最小值.
【难度】★
【答案】
【解析】如图,设该圆锥底面半径为,高为,并设球心切母线于。则∽。
∴,即,∴。
令,则,当且仅当时,等号成立。
故,此时。
3.将半径为R的五个球中的四个放在桌面上,使每相邻两个球相切,第五个球放在四个球上,使它与这四个球都相切,则这第五个球球心到桌面的距离为 .
【难度】★★
【答案】
4.球面上三点组成这个球的一个截面的内接三角形,,且球心到该截面的距离为球的半径的一半,
(1)求球的体积; (2)求两点的球面距离.
【难度】★★
【答案】;
球面距离的计算需要先搞清楚经度、纬度、大圆、小圆等概念,然后计算过两点的大圆的圆弧(劣弧)长度。常见的有同赤道,同经度、同纬度几种,经度纬度都不同的情况较难,但是原理是相同的.
计算球的表面积和体积主要利用前面所学的立体几何知识,求出球的半径,然后使用相应公式计算即可.
在球的有关问题中,常见球内接几何体或者球外切几何体的问题.球内接几何体的问题中,球内接棱柱的体对角线为球的直径,这是解决这一类问题的关键点;球外切几何体的问题,一般与球的直径垂直于面相关.
1.面半径2R的圆柱形铁罐做一种半径为R的球型产品的外包装,一听4个,铁罐的高度至少应为 .
【难度】★★
【答案】2R
2.圆柱形容器内盛有高度为的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是________
【难度】★★
【答案】
【解析】设球的半径为,则.解得.
3.圆锥的高为,侧面积为,其内切球的表面积为________.
【难度】★★
【答案】
【解析】设圆锥底面半径为,则母线长,由得,解之得,∴.设内切球半径为,作出圆锥的轴截面如图,则,,,,
∴球的表面积.
4.半径为的球内部装有个半径相同的小球,则小球半径的可能最大值为(??).
A. B. B. D.
【难度】★★
【答案】
5.已知三棱锥的所有顶点都在球的球面上,是边长为的正三角形,为球的直径,且,则此棱锥的体积为( )
A. B. C. D.
【难度】★★
【答案】A
【解析】如图,为的外接圆圆心,则,设的外接圆半径为,
则,
∴.连接,根据球的截面性质知,
,为的中点,∴到平面的距离为,∴
6.点在同一个球的球面上,,若四面体体积的最大值为,则这个球的表面积为( )
A. B. C. D.
【难度】★★
【答案】
【解析】如图所示,为球的球心,由可知,即所在的小圆的圆心1为的中点,故,当为的延长线与球面的交点时,到平面的距离最大,四面体的体积最大.连接,设球的半径为,则,此时,解得,故这个球的表面积为=.
7.若一个正四面体的表面积为,其内切球的表面积为,则=________.
【难度】★★
【答案】
【解析】设正四面体棱长为,则正四面体表面积为,其内切球半径为正四面体高的,即,因此内切球表面积为,则.
8.如图,直三棱柱的六个顶点都在半径为的半球面上,,侧面是半球底面圆的内接正方形,则侧面的面积为( )
【难度】★★
【答案】
【解析】由题意知,球心在侧面的中心上,为截面圆的直径,∴,的外接圆圆心是的中点,同理的外心是的中心.设正方形的边长为,中,(为球的半径),∴,即,则,∴矩形.
9.一个正方体削去一个角所得到的几何体的三视图如图所示(图中三个四边形都是边长为的正方形),则该几何体外接球的体积为________.
【难度】★★
【答案】
【解析】依题意可知,新的几何体的外接球也就是原正方体的外接球,要求的直径就是正方体的体对角线;∴(为球的半径),∴,∴球的体积.
10.正四棱锥的顶点都在同一球面上,若该棱锥的高为,底面边长为,则该球的表面积为( )
【难度】★★
【答案】
【解析】如图所示,设球半径为,底面中心为且球心为,∵正四棱锥中∵,∴在中,,∴,解得,∴该球的表面积为,故选.
