4.1 比例的意义和基本性质(复习课)(共21张PPT)
文档属性
| 名称 | 4.1 比例的意义和基本性质(复习课)(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 665.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 07:07:44 | ||
图片预览








文档简介
(共21张PPT)
人教版 六年级数学下册
第4单元 比例
4.1 比例的意义和基本性质
复习课
学习目标
1.理解比例的意义
2.掌握比例的基本性质
3.会利用比例的基本性质熟练解比例,并解决实际问题。
2、在3:15、9:45、4:3三个比中,选择其中两个比组成比例.
1、18:30和3:5可以组成比例吗?
表示两个比相等的式子叫做比例.
解:因为
所以18:30和3:5可以组成比例
解:因为
所以3:15和9:45可以组成比例
一、比例的意义
1.下列各式是比例的是( )
A.4+3=3+4 B.4 : 0.8=5 : 1
C.27÷9=1×3 D.5 : 3=0.6
B
2. 5∶3=15∶9的内项3增加6,要使比例成立,外项9应增加( )
3.下面的比中能与3∶8组成比例的是( )。
A.3.5∶6 B. 6:1.5 C. 1.5:4 D.5:2
针对训练
B
5:9=15:27
C
A.6 B.18 C.27 D.9
1.如果A:7=9:B,那么AB=( )
2.在一个比例中,两个外项互为倒数,如果一个内项是2.5,则另一个内项是( )
二、比例的基本性质
3.应用比例的基本性质,判断下面哪组中的两个比可以组成比例.
63
0.4
√
×
用字母表示比例的基本性质:
a∶b=c∶d(b、d≠0)
=
或
ad=bc
二、比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质
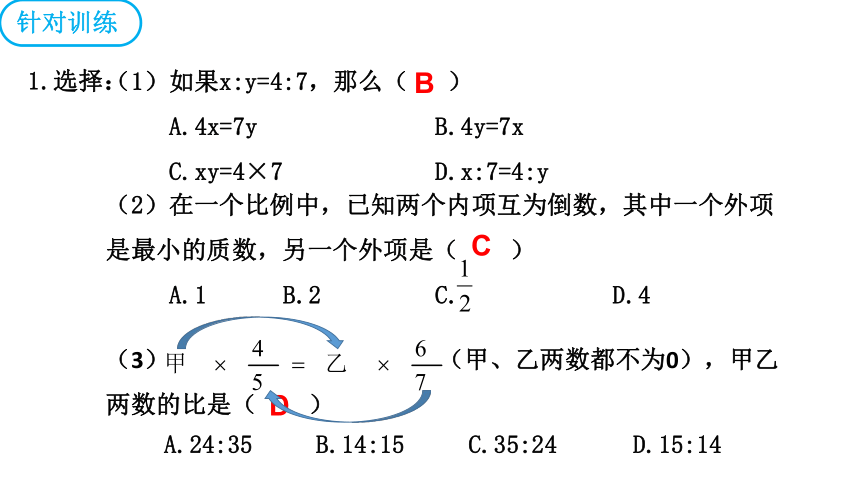
(2)在一个比例中,已知两个内项互为倒数,其中一个外项是最小的质数,另一个外项是( )
A.1 B.2 C. D.4
(1)如果x:y=4:7,那么( )
A.4x=7y B.4y=7x
C.xy=4×7 D.x:7=4:y
B
C
(3)甲数的 等于乙数的 (甲、乙两数都不为0),甲乙两数的比是( )
1.选择:
针对训练
D
A.24:35 B.14:15 C.35:24 D.15:14
2.判断:
(1)在比例里,两个外项的积与两个内项的积的差等于0.( )
(2)如果 ,那么 .( )
√
×
(3)如果4X=3Y,(X和Y均不为0),那么4:X=3:Y. ( )
(4)因为3×10=5×6,所以3:5=10:6. ( )
×
×
针对训练
(1)如果 ( ),那么
(2)如果 ,那么 ( ) ﹕ ( ).
3.填空:
(3)已知 A÷10.5=7÷B(A与B都不为0),则A与B的积是( ).
(4)X:Y=3:4,Y:Z=6:5,X:Y:Z=( )
针对训练
( )
( )
7
2
b
1
A:10.5=7:B
73.5
X:Y=9:12
Y:Z=12:10
9:12:10
根据比例的基本性质,如果已知比例中任意三项,就可以求出这个比例中的另外一个未知项。
4.根据条件列出比例:
针对训练
三、解比例
解:
解:
解比例的方法:
先把比例转化成外项乘积与内项乘积相等的形式(即方程)
一般要把含有x的乘积写在等号的左边
再通过解方程求出未知项的值。
大家回想一下,什么叫解比例?
解比例的方法是什么?
三、解比例
求比例中的未知项,叫做解比例.
1. 解比例
解:
解:
解:
针对训练
解:
2.解决问题:
(1)2013年5月22日,中华鲟纪念币和白鳍豚纪念币的价格比是2:3,每枚中华鲟纪念币的价格是50元,每枚白鳍豚纪念币的价格是多少元?
50:x=2:3
解:设每枚白鳍豚纪念币的价格是x元。
2x=50×3
2x=150
答:每枚白鳍豚纪念币的价格是75元。
x=75
1、写“解”,设未知项为 x
2、根据题意列出一个比例
3、解比例
4、写答
针对训练
(2)中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
树高:树的影长=人高:人的影长
树高:人高=树的影长:人的影长
针对训练
x:10=1.5:0.5
解:设它的高度是x 米。
0.5x=10×1.5
0.5x=15
答:它的高度是30米。
x=30
(2)中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
针对训练
树高:树的影长=人高:人的影长
x:1.5=10:0.5
解:设它的高度是x 米。
0.5x=10×1.5
0.5x=15
答:它的高度是30米。
x=30
(2)中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
针对训练
树高:人高=树的影长:人的影长
(3)某种首饰是将金和铂按5∶1的比例熔铸而成,其中金
的含量比铂多32 g ,这种首饰中金和铂各多少克?
解:设这种首饰中金有x 克,铂有(x -32 )克。
答:这种首饰中金有40克,铂有8克。
针对训练
x :(x -32)=5:1
5(x -32)=x
5x -160=x
5x -x =160
4x =160
x =40
x -32=8
比 例
比例的意义
比例的基本性质
解 比 例
方法
实际问题
设未知数
列比例
解比例
写答
转化成乘积相等的形式
一般把含有x的项写在等号左边
解方程
小 结
1.在下面的括号里填上适当的数。
家庭作业
( )
( ):0.5
2.甲数的 等于乙数的 (甲、乙两数都不为0),甲乙两数的比是( ).
3.在一个比例中,两个外项互为倒数,如果一个内项是2.25,则另一个内项是( )。
4. x:y=6:8,y:z=3:4,则x:z=( )
5.解比例
家庭作业
6.配制一种农药,其中药与水的质量比为1∶150。
(1)如果有525 g水,要配制这种农药,需要放进多少克的药?
(2)如果有3 g药,能配制这种农药多少克?
人教版 六年级数学下册
第4单元 比例
4.1 比例的意义和基本性质
复习课
学习目标
1.理解比例的意义
2.掌握比例的基本性质
3.会利用比例的基本性质熟练解比例,并解决实际问题。
2、在3:15、9:45、4:3三个比中,选择其中两个比组成比例.
1、18:30和3:5可以组成比例吗?
表示两个比相等的式子叫做比例.
解:因为
所以18:30和3:5可以组成比例
解:因为
所以3:15和9:45可以组成比例
一、比例的意义
1.下列各式是比例的是( )
A.4+3=3+4 B.4 : 0.8=5 : 1
C.27÷9=1×3 D.5 : 3=0.6
B
2. 5∶3=15∶9的内项3增加6,要使比例成立,外项9应增加( )
3.下面的比中能与3∶8组成比例的是( )。
A.3.5∶6 B. 6:1.5 C. 1.5:4 D.5:2
针对训练
B
5:9=15:27
C
A.6 B.18 C.27 D.9
1.如果A:7=9:B,那么AB=( )
2.在一个比例中,两个外项互为倒数,如果一个内项是2.5,则另一个内项是( )
二、比例的基本性质
3.应用比例的基本性质,判断下面哪组中的两个比可以组成比例.
63
0.4
√
×
用字母表示比例的基本性质:
a∶b=c∶d(b、d≠0)
=
或
ad=bc
二、比例的基本性质
在比例里,两个外项的积等于两个内项的积,这叫做比例的基本性质
(2)在一个比例中,已知两个内项互为倒数,其中一个外项是最小的质数,另一个外项是( )
A.1 B.2 C. D.4
(1)如果x:y=4:7,那么( )
A.4x=7y B.4y=7x
C.xy=4×7 D.x:7=4:y
B
C
(3)甲数的 等于乙数的 (甲、乙两数都不为0),甲乙两数的比是( )
1.选择:
针对训练
D
A.24:35 B.14:15 C.35:24 D.15:14
2.判断:
(1)在比例里,两个外项的积与两个内项的积的差等于0.( )
(2)如果 ,那么 .( )
√
×
(3)如果4X=3Y,(X和Y均不为0),那么4:X=3:Y. ( )
(4)因为3×10=5×6,所以3:5=10:6. ( )
×
×
针对训练
(1)如果 ( ),那么
(2)如果 ,那么 ( ) ﹕ ( ).
3.填空:
(3)已知 A÷10.5=7÷B(A与B都不为0),则A与B的积是( ).
(4)X:Y=3:4,Y:Z=6:5,X:Y:Z=( )
针对训练
( )
( )
7
2
b
1
A:10.5=7:B
73.5
X:Y=9:12
Y:Z=12:10
9:12:10
根据比例的基本性质,如果已知比例中任意三项,就可以求出这个比例中的另外一个未知项。
4.根据条件列出比例:
针对训练
三、解比例
解:
解:
解比例的方法:
先把比例转化成外项乘积与内项乘积相等的形式(即方程)
一般要把含有x的乘积写在等号的左边
再通过解方程求出未知项的值。
大家回想一下,什么叫解比例?
解比例的方法是什么?
三、解比例
求比例中的未知项,叫做解比例.
1. 解比例
解:
解:
解:
针对训练
解:
2.解决问题:
(1)2013年5月22日,中华鲟纪念币和白鳍豚纪念币的价格比是2:3,每枚中华鲟纪念币的价格是50元,每枚白鳍豚纪念币的价格是多少元?
50:x=2:3
解:设每枚白鳍豚纪念币的价格是x元。
2x=50×3
2x=150
答:每枚白鳍豚纪念币的价格是75元。
x=75
1、写“解”,设未知项为 x
2、根据题意列出一个比例
3、解比例
4、写答
针对训练
(2)中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
树高:树的影长=人高:人的影长
树高:人高=树的影长:人的影长
针对训练
x:10=1.5:0.5
解:设它的高度是x 米。
0.5x=10×1.5
0.5x=15
答:它的高度是30米。
x=30
(2)中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
针对训练
树高:树的影长=人高:人的影长
x:1.5=10:0.5
解:设它的高度是x 米。
0.5x=10×1.5
0.5x=15
答:它的高度是30米。
x=30
(2)中午,太阳当头照。小明身高1.5m,他的影子长0.5m。
一棵松树的影子长10m,它的高度是多少米呢?
针对训练
树高:人高=树的影长:人的影长
(3)某种首饰是将金和铂按5∶1的比例熔铸而成,其中金
的含量比铂多32 g ,这种首饰中金和铂各多少克?
解:设这种首饰中金有x 克,铂有(x -32 )克。
答:这种首饰中金有40克,铂有8克。
针对训练
x :(x -32)=5:1
5(x -32)=x
5x -160=x
5x -x =160
4x =160
x =40
x -32=8
比 例
比例的意义
比例的基本性质
解 比 例
方法
实际问题
设未知数
列比例
解比例
写答
转化成乘积相等的形式
一般把含有x的项写在等号左边
解方程
小 结
1.在下面的括号里填上适当的数。
家庭作业
( )
( ):0.5
2.甲数的 等于乙数的 (甲、乙两数都不为0),甲乙两数的比是( ).
3.在一个比例中,两个外项互为倒数,如果一个内项是2.25,则另一个内项是( )。
4. x:y=6:8,y:z=3:4,则x:z=( )
5.解比例
家庭作业
6.配制一种农药,其中药与水的质量比为1∶150。
(1)如果有525 g水,要配制这种农药,需要放进多少克的药?
(2)如果有3 g药,能配制这种农药多少克?
