人教版七年级数学下册6.1平方根课件(共51张PPT)
文档属性
| 名称 | 人教版七年级数学下册6.1平方根课件(共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 509.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-08 00:00:00 | ||
图片预览




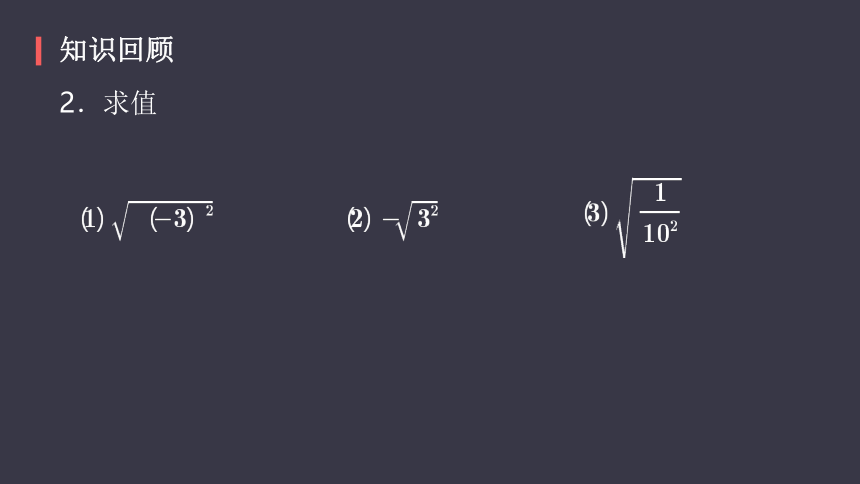





文档简介
(共51张PPT)
平方根
教学目标
了解平方根的概念;掌握平方根的特征.?
能利用开平方与平方互为逆运算的关系, 求某些非负数的平方根.
教学重点
平方根的概念.
教学难点
平方根和算术平方根的联系与区别.
1、求下列各数的算术平方根
知识回顾
(1)196? ? ? ? ? ? ? ? ? ? (2)0.04? ? ? ? ? ? ? ? ? ? ?(3)10?
2.求值
知识回顾
如果一个数的平方等于9,这个数是多少?
思考
由于? ? ? ? ? ? ? ? ? ? ? ?,
所以这个数是3或-3.
这里的3是前面学过的 9 的_____________.
-3与 9 的算术平方根有什么关系?
-3与 9 的算术平方根互为相反数.
算术平方根
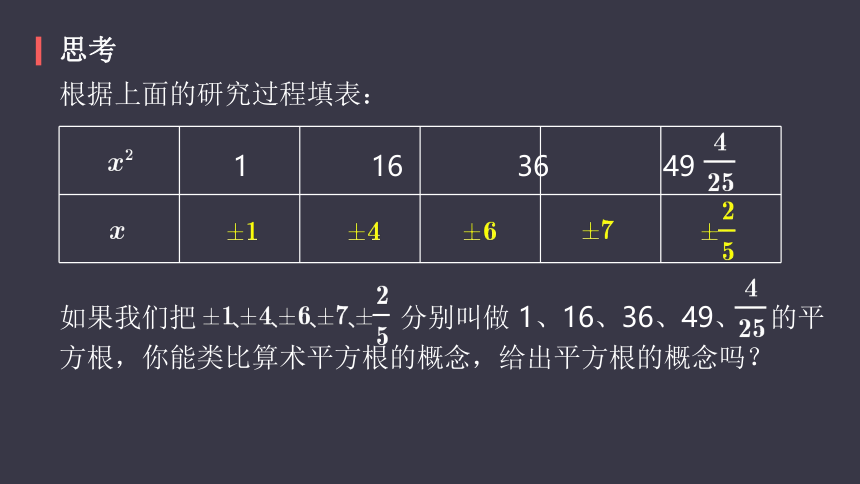
根据上面的研究过程填表:
思考
如果我们把 ?? ? ? ? ? ? ? 分别叫做? ? ? ? ? ? 的平方根,你能类比算术平方根的概念,给出平方根的概念吗?
1、16、36、49、
1? ? ? ? ? ? ? ?16? ? ? ? ? ? ? 36? ? ? ? ? ? ? 49
如果一个数的平方等于 a ,这个数叫a的平方根或二次方根.
平方根的概念
如果 x? ?= a,那么 x 叫做 a 的平方根.
例如,3和-3是9的平方根,简记为±3是9的平方根.
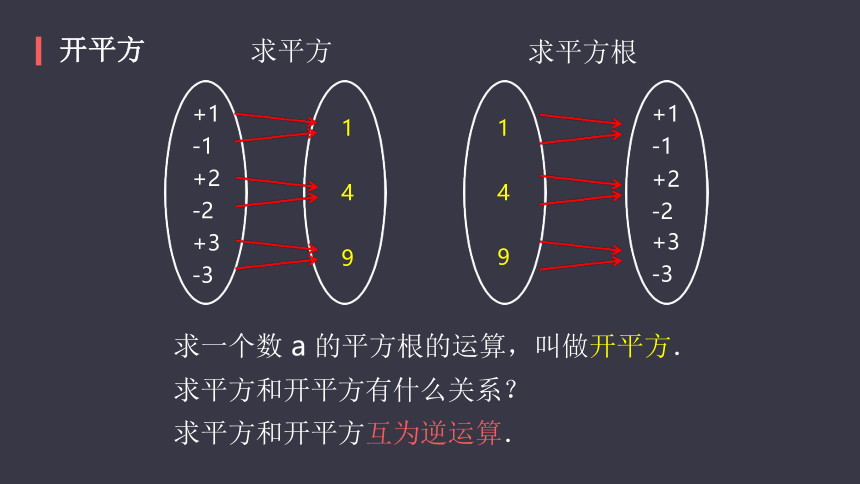
求平方
求平方根?
开平方
求一个数 a 的平方根的运算,叫做开平方.
求平方和开平方有什么关系?
求平方和开平方互为逆运算.
+1
-1
+2
-2
+3
-3
1
1
4
9
+1
-1
4
9
+2
-2
+3
-3
求下列各数的平方根:
例题
解:(1)因为? ? ? ? ? ? ? ? ? ? ? 所以100的平方根是
求下列各数的平方根:
练习
(2)0.
(2)因为? ? ? ? ? ? ,所以 0 的平方根是 0.
判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是? ? ? ? ;
(5)-16的平方根是-4.
练习
正数的平方根有什么特点?
思考
正数的平方根有两个,它们互为相反数.
0的平方根是多少?
因为只有0的平方等于0,所以0的平方根是0.
负数有平方根吗?
因为任何数的平方都不可能是负数,所以负数没有平方根.
正数的平方根有两个,它们互为相反数.
0的平方根是0;
平方根的性质
负数没有平方根.
你知道怎么表示一个正数 a 的平方根吗?
平方根的表示
正数a的算术平方根可以表示用_____表示;
正数a的负的平方根,可以用符号______表示,
正数a的平方根用符号________表示.
读作“正、负根号a”.
例如,
符号? ? ? ?有意义的条件是什么?
平方根的表示
表示 a 的算术平方根.
任何数的平方都不可能是负数,所以负数没有算术平方根,
所以当a≥0时有意义,a<0时无意义.
表示 a 的______________.
算术平方根
平方根和算式平方根的区别
表示 a 的__________.
平方根
口诀:平方根有正负,算术平方根无正负.
前有符号,结果就_____符号.
前无符号,结果就_____符号.
有
无
判断下列各式计算是否正确,并说明理由.
例题
总结:化简前后的________要保持一致.
符号
说出下列各式的意义,并求它们的值:
例题
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
正数的两个平方根互为相反数.
1.判断下列说法是否正确:
练习
(1)0的平方根是0;
(2)1的平方根式1;
(3)-1的平方根式-1;
(4)0.01是0.1的一个平方根.
2.填表:
练习
x? ? ? ? ? ?8? ? ? ? -8
16? ? ? ? ? ? ? ? ? ?0.36
练习
3.计算下列各式的值:
练习
4.平方根概念的起源与几何中的正方形有关.如果一个正方形的面积为A,那么这个正方形的边长是多少?
判断下列各数有没有平方根,如果有平方根,试求出它的平方根 ;如果没有平方根,说明理由.
练习
(1)81? ? ? ? ? ? ? ? ?(2)-81
(3)0? ? ? ? ? ? ? ? ? ?(4)0.0001
(5)? ? ? ? ? ? ? ? ? ? ?(6)?
练习
说出下列各式的意义,并求值.
=12
=-0.06
=5+6
=11
练习
已知 ??2a-1 的平方根是±3 ??,3a+b-1?? 的算术平方根是 ??4 ,求a+2b?? 的值 .
答案:9.
判断下面的说法是否正确,如不正确,说明理由,并加以改正.
易错题
(1)-3 的平方根是 9? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(2)9 的平方根是-3? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (? ? ? ? )
(3)3 是 9 的平方根? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(4)4的平方根是±2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(5)-5是25的平方根? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(6)-1的平方根是±1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (? ? ? ? )
(7)(-10)? ? 没有平方根? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (? ? ? ? )
(8)如果 x? ? = a,则 a 一定是正数? ? ? ? ? (? ? ? ? )
易错题
(1)平方根是本身的数只有________ ;??
(2)一个数的平方等于它本身,这个数是________ ;??
(3)一个数的算术平方根等于它本身,这个数是_______ .
0
0、1
0、1
易错题
的平方根是_______.
有一个正数的两个平方根是2m-3和5-m,求m的值.
利用平方根互为相反数解题
解:由题意得? ? ? ?
? ? ? (2m-3)+(5-m)=0
∴ m=-2
有一个正数的两个平方根是a+1和2a-7,求这个正数的值.
利用平方根互为相反数解题
答案:9.
求下列各式中的 x:
解二次方程
答案:(1)±9;(2)6或-4.
求下列各式中的 x:
解二次方程
答案:
如果? ? ? ? ? ? ? ? ? ? ,求2x+5的算术平方根.
解根式方程
答案:3.
解根式方程
256
的整数部分和小数部分是多少?
整数部分和小数部分
答案:? ? ? ?的整数部分是3,小数部分是? ? ? ? ? ? ? ? .
总结:原数减去整数部分所得就是小数部分.
确定? ? ? ? ? ?整数部分和小数部分是多少?
整数部分和小数部分
答案:? ? ? ? ?的整数部分是5,小数部分是? ? ? ? ? ? ?.
确定? ? ? ? ? ? ?整数部分和小数部分是多少?
整数部分和小数部分
答案:? ? ? ? ? ? ?的整数部分是3,小数部分是? ? ? ? ? ? ? .
这节课我们学会了什么?
总结
1.平方根的概念:
如果一个数的平方等于 a ,这个数叫a的平方根或二次方根.
如果 x? ? = a,那么 x 叫做 a 的平方根.
2.平方根的性质:
正数的平方根有两个,它们互为相反数.
0的平方根是0;
负数没有平方根.
3.平方根与算术平方根的区别:
这节课我们学会了什么?
总结
表示 a 的______________.
算术平方根
表示 a 的__________.
平方根
口诀:平方根有正负,算术平方根无正负.
复习巩固
1.求下列各数的算术平方根:
(1)81;
(3)0.04;
复习巩固
2.下列各式是否有意义,为什么?
复习巩固
3.求下列各数的平方根:
(1)49;
(4)0.0016.
复习巩固
4.判断下列说法是否正确:
(1)5是25的算术平方根;
(4)0的平方根与算术平方根都是0.
复习巩固
5.用计算器计算下列各式的值(精确到0.01):
复习巩固
6.估计与? ? ? ? ?最接近的两个整数是多少?
综合运用
8.求下列各式中 x 的值:
综合运用
9.自由下落物体高度h(单位:m)与下落时间t(单位:s)的关系是h=4.9t? ? .如图,有一个物体从120m高的建筑物上自由下落,到达地面需要多长时间(结果取整数)?
综合运用
10.一个正方形的面积扩大为原来的4倍,它的边长变为原来的多少倍?面积扩大为原来的9倍呢?n倍呢?
拓广探索
11.(1)求
的值,对于任意数a,
(2)求
的值,对于任意非负数a,
拓广探索
12.任意找一个正数,比如1234,利用计算器对它进行开平方,再对得到的算术平方根进行开平方.......如此进行下去,你有什么发现?
平方根
教学目标
了解平方根的概念;掌握平方根的特征.?
能利用开平方与平方互为逆运算的关系, 求某些非负数的平方根.
教学重点
平方根的概念.
教学难点
平方根和算术平方根的联系与区别.
1、求下列各数的算术平方根
知识回顾
(1)196? ? ? ? ? ? ? ? ? ? (2)0.04? ? ? ? ? ? ? ? ? ? ?(3)10?
2.求值
知识回顾
如果一个数的平方等于9,这个数是多少?
思考
由于? ? ? ? ? ? ? ? ? ? ? ?,
所以这个数是3或-3.
这里的3是前面学过的 9 的_____________.
-3与 9 的算术平方根有什么关系?
-3与 9 的算术平方根互为相反数.
算术平方根
根据上面的研究过程填表:
思考
如果我们把 ?? ? ? ? ? ? ? 分别叫做? ? ? ? ? ? 的平方根,你能类比算术平方根的概念,给出平方根的概念吗?
1、16、36、49、
1? ? ? ? ? ? ? ?16? ? ? ? ? ? ? 36? ? ? ? ? ? ? 49
如果一个数的平方等于 a ,这个数叫a的平方根或二次方根.
平方根的概念
如果 x? ?= a,那么 x 叫做 a 的平方根.
例如,3和-3是9的平方根,简记为±3是9的平方根.
求平方
求平方根?
开平方
求一个数 a 的平方根的运算,叫做开平方.
求平方和开平方有什么关系?
求平方和开平方互为逆运算.
+1
-1
+2
-2
+3
-3
1
1
4
9
+1
-1
4
9
+2
-2
+3
-3
求下列各数的平方根:
例题
解:(1)因为? ? ? ? ? ? ? ? ? ? ? 所以100的平方根是
求下列各数的平方根:
练习
(2)0.
(2)因为? ? ? ? ? ? ,所以 0 的平方根是 0.
判断下列说法是否正确,并说明理由.
(1)49的平方根是7;
(2)2是4的平方根;
(3)-5是25的平方根;
(4)64的平方根是? ? ? ? ;
(5)-16的平方根是-4.
练习
正数的平方根有什么特点?
思考
正数的平方根有两个,它们互为相反数.
0的平方根是多少?
因为只有0的平方等于0,所以0的平方根是0.
负数有平方根吗?
因为任何数的平方都不可能是负数,所以负数没有平方根.
正数的平方根有两个,它们互为相反数.
0的平方根是0;
平方根的性质
负数没有平方根.
你知道怎么表示一个正数 a 的平方根吗?
平方根的表示
正数a的算术平方根可以表示用_____表示;
正数a的负的平方根,可以用符号______表示,
正数a的平方根用符号________表示.
读作“正、负根号a”.
例如,
符号? ? ? ?有意义的条件是什么?
平方根的表示
表示 a 的算术平方根.
任何数的平方都不可能是负数,所以负数没有算术平方根,
所以当a≥0时有意义,a<0时无意义.
表示 a 的______________.
算术平方根
平方根和算式平方根的区别
表示 a 的__________.
平方根
口诀:平方根有正负,算术平方根无正负.
前有符号,结果就_____符号.
前无符号,结果就_____符号.
有
无
判断下列各式计算是否正确,并说明理由.
例题
总结:化简前后的________要保持一致.
符号
说出下列各式的意义,并求它们的值:
例题
如果知道一个数的算术平方根就可以立即写出它的负的平方根,为什么?
正数的两个平方根互为相反数.
1.判断下列说法是否正确:
练习
(1)0的平方根是0;
(2)1的平方根式1;
(3)-1的平方根式-1;
(4)0.01是0.1的一个平方根.
2.填表:
练习
x? ? ? ? ? ?8? ? ? ? -8
16? ? ? ? ? ? ? ? ? ?0.36
练习
3.计算下列各式的值:
练习
4.平方根概念的起源与几何中的正方形有关.如果一个正方形的面积为A,那么这个正方形的边长是多少?
判断下列各数有没有平方根,如果有平方根,试求出它的平方根 ;如果没有平方根,说明理由.
练习
(1)81? ? ? ? ? ? ? ? ?(2)-81
(3)0? ? ? ? ? ? ? ? ? ?(4)0.0001
(5)? ? ? ? ? ? ? ? ? ? ?(6)?
练习
说出下列各式的意义,并求值.
=12
=-0.06
=5+6
=11
练习
已知 ??2a-1 的平方根是±3 ??,3a+b-1?? 的算术平方根是 ??4 ,求a+2b?? 的值 .
答案:9.
判断下面的说法是否正确,如不正确,说明理由,并加以改正.
易错题
(1)-3 的平方根是 9? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(2)9 的平方根是-3? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (? ? ? ? )
(3)3 是 9 的平方根? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(4)4的平方根是±2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(5)-5是25的平方根? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?(? ? ? ? )
(6)-1的平方根是±1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (? ? ? ? )
(7)(-10)? ? 没有平方根? ? ? ? ? ? ? ? ? ? ? ? ? ? ? (? ? ? ? )
(8)如果 x? ? = a,则 a 一定是正数? ? ? ? ? (? ? ? ? )
易错题
(1)平方根是本身的数只有________ ;??
(2)一个数的平方等于它本身,这个数是________ ;??
(3)一个数的算术平方根等于它本身,这个数是_______ .
0
0、1
0、1
易错题
的平方根是_______.
有一个正数的两个平方根是2m-3和5-m,求m的值.
利用平方根互为相反数解题
解:由题意得? ? ? ?
? ? ? (2m-3)+(5-m)=0
∴ m=-2
有一个正数的两个平方根是a+1和2a-7,求这个正数的值.
利用平方根互为相反数解题
答案:9.
求下列各式中的 x:
解二次方程
答案:(1)±9;(2)6或-4.
求下列各式中的 x:
解二次方程
答案:
如果? ? ? ? ? ? ? ? ? ? ,求2x+5的算术平方根.
解根式方程
答案:3.
解根式方程
256
的整数部分和小数部分是多少?
整数部分和小数部分
答案:? ? ? ?的整数部分是3,小数部分是? ? ? ? ? ? ? ? .
总结:原数减去整数部分所得就是小数部分.
确定? ? ? ? ? ?整数部分和小数部分是多少?
整数部分和小数部分
答案:? ? ? ? ?的整数部分是5,小数部分是? ? ? ? ? ? ?.
确定? ? ? ? ? ? ?整数部分和小数部分是多少?
整数部分和小数部分
答案:? ? ? ? ? ? ?的整数部分是3,小数部分是? ? ? ? ? ? ? .
这节课我们学会了什么?
总结
1.平方根的概念:
如果一个数的平方等于 a ,这个数叫a的平方根或二次方根.
如果 x? ? = a,那么 x 叫做 a 的平方根.
2.平方根的性质:
正数的平方根有两个,它们互为相反数.
0的平方根是0;
负数没有平方根.
3.平方根与算术平方根的区别:
这节课我们学会了什么?
总结
表示 a 的______________.
算术平方根
表示 a 的__________.
平方根
口诀:平方根有正负,算术平方根无正负.
复习巩固
1.求下列各数的算术平方根:
(1)81;
(3)0.04;
复习巩固
2.下列各式是否有意义,为什么?
复习巩固
3.求下列各数的平方根:
(1)49;
(4)0.0016.
复习巩固
4.判断下列说法是否正确:
(1)5是25的算术平方根;
(4)0的平方根与算术平方根都是0.
复习巩固
5.用计算器计算下列各式的值(精确到0.01):
复习巩固
6.估计与? ? ? ? ?最接近的两个整数是多少?
综合运用
8.求下列各式中 x 的值:
综合运用
9.自由下落物体高度h(单位:m)与下落时间t(单位:s)的关系是h=4.9t? ? .如图,有一个物体从120m高的建筑物上自由下落,到达地面需要多长时间(结果取整数)?
综合运用
10.一个正方形的面积扩大为原来的4倍,它的边长变为原来的多少倍?面积扩大为原来的9倍呢?n倍呢?
拓广探索
11.(1)求
的值,对于任意数a,
(2)求
的值,对于任意非负数a,
拓广探索
12.任意找一个正数,比如1234,利用计算器对它进行开平方,再对得到的算术平方根进行开平方.......如此进行下去,你有什么发现?
