人教版七年级数学下册7.2.2用坐标表示平移课件(共62张PPT)
文档属性
| 名称 | 人教版七年级数学下册7.2.2用坐标表示平移课件(共62张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 00:00:00 | ||
图片预览











文档简介
(共62张PPT)
用坐标表示平移
掌握点或图形的平移引起点的坐标的变化规律.??
会根据图形上点的坐标的某种变化,得出图形进行了怎样的平移.
教学目标
教学重点
教学难点
在平面直角坐标系中,图形平移变化中坐标的变化规律.??
图形平移与其坐标变化之间的关系.
在平面直角坐标系中,探究点的坐标的某种变化引起的图形平移.
知识回顾
1、平移的定义
在平面内,将一个图形沿____________移动一定的距离,这样的图形运动称为平移.
2、平移的性质
(1)平移不改变图形的_____________, 只改变形图形的______.
(2)经过平移后,对应点所连的线段 _____________.
某个方向
形状和大小
位置
平行且相等
探究
点的平移
(-2,-3)
(-2,-3)
(-2,-3)
(-2,-3)
(3,-3)
(-4,-3)
(-2,3)
(-2,-7)
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢?
把点A向上平移6个单位呢?
把点A向下平移4个单位呢?
右移5个单位
横坐标+5
左移2个单位
横坐标-2
上移6个单位
纵坐标+6
下移4个单位
纵坐标-4
平移前后的坐标有什么关系?
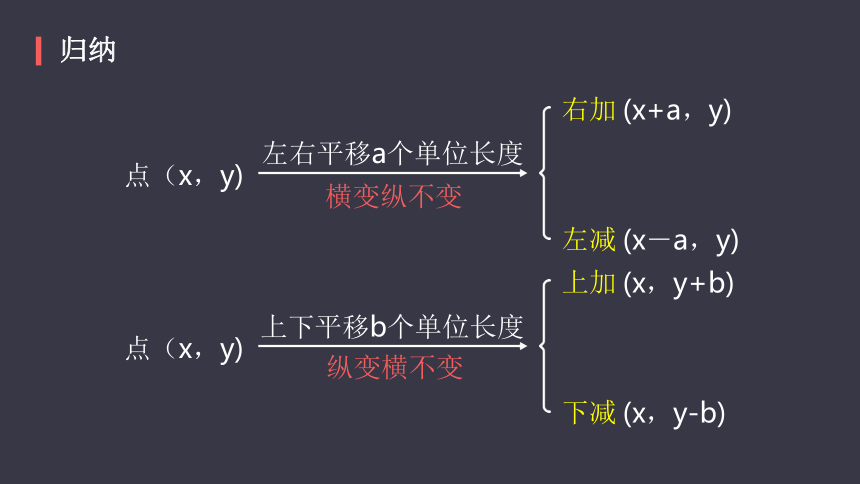
归纳
点(x,y)
左右平移a个单位长度
横变纵不变
右加
(x+a,y)
左减
(x-a,y)
上下平移b个单位长度
纵变横不变
上加
下减
(x,y+b)
(x,y-b)
点(x,y)
例题
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线.
先向下平移5个单位长度,
再向左平移3个单位长度.
先向左平移3个单位长度,
再向下平移5个单位长度.
1.将点A(3,2)向上平移2个单位长度,得到A’,则A’的坐标为______.??
2.将点A(3,2)向下平移3个单位长度,得到A’,则A’的坐标为________.?
3.将点A(3,2)向左平移4个单位长度,得到A’,则A’的坐标为________.?
4.将点A(3,2)向右平移2个单位长度,得到A’,则A’的坐标为______.
练习
(3,4)
(3,-1)
(-1,2)
(5,2)
(1)将点A(0,-8)向上平移2个单位长度,得到A’,则A’的坐标为___________.
练习
(2)将点A(2,-1)向左平移4个单位长度,得到A’,则A’的坐标为___________.
(0,-6)
(-2,-1)
练习
1、点P(2,-1)向左平移3个单位长度得点Q的坐标为________.
2、点P(2,-1)向上平移2个单位长度得点Q的坐标为________.
3、点P(2,-1)向右平移3个单位长度,再向下平移2个单位长度得点Q的坐标为___________.
(-1,-1 )
( 2,1 )
( 5,-3 )
练习
已知点A(3,2),将点A先向右平移2个单位长度,再向上平移5个单位长度,得到A′,则A′的坐标为________.
(5,7)
练习
将点P(0,-2)向左平移2个单位,再向上平移4个单位得点Q(x,y),则xy=_____.
-4
1.把点M(1,2)平移后得到点N(1,-2) ,则平移的过程是:_________________.
2.把点M(-3,1)平移后得到点N(-1,4),则平移的过程是:_______________________________________________________.
向下平移4个单位
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
练习——求平移量
练习——反求
将点P(m,1)向右平移5个单位长度,得到点Q(3,1),则点P坐标为___________.
(-2,1)
练习——反求
将点M(a,b)向左平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,-6),则a=____,b=____.
3
-3
练习
将点P(m+2,2m+4)向右平移1个单位得到P’,且P’在y轴上,那么P’坐标是(? ? ? ? ) .
A.(-2,0)??
B.(0,-2)?
C.(1,0)?
D.(0,1)
B
探究
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.
(1)点E,F,G,H的坐标分别是什么?
E(6,-3),F(6,-4),G(7,-4),H(7,-3).
探究
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.??
(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
归纳
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图示上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
例题
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,点A1,B1,C1坐标分别是什么?并画出相应的三角形A1B1C1?.
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
例题
三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系?
大小和形状不变,
思考
△ A1B1C1可以看做△ABC向左平移6个单位长度得到的.
例题
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,点A2,B2,C2坐标分别是什么?并画出相应的三角形A2B2C2.
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
例题
三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
大小和形状不变,
思考
△ A2B2C2可以看做△ABC向下平移5个单位长度得到的.
例题
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
如图,将三角形ABC三个顶点的横坐标都减去 6,同时纵坐标减去5,又能得到什么结论?
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
例题
三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
大小和形状不变,
思考
可以发现所得三角形可以由三角形ABC向左平移6个单位长度,再向下平移了5个单位长度.?
归纳总结
图形上点的坐标变化与图形移动的关系
横坐标都加a
横坐标都减a
纵坐标都加a
纵坐标都减a
图形向右平移a
图形向左平移a
图形向上平移a
图形向下平移a
练习
将平行四边形ABCD向左平移2个单位长度,向上平移3个单位长度,可以得到平行四边形A'B'C'D',画出平移后的图形,并指出其各个顶点的坐标.
各个顶点的坐标是
A'(-3,1);
B'(1,1);
C'(2,4);
D'(-2,4).
练习
已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是
(? ? ?).?
(A)(5,-2)
(B)(1,-2)
(C)(2,-1)
(D)(2,-2)
B
练习
如图,△ABC的三个顶点的坐标分别是A(-4,-1),B(-5,-4),C(-1,-3),将这三点的横坐标加6,同时纵坐标加4,分别得到点A',B',C',依次连接A',B',C'各点,说明△A'B'C'可以由△ABC沿坐标轴方向平移得到.
补充题
已知图形上一点的坐标变化
平移一个图形时,图形上所有点的坐标变化_______ ,
所以已知一点的坐标变化, 就能得到其他所有点的坐标变化.
相同
已知图形上一点的坐标变化
如图,已知铅笔尖平移前后的坐标分别为(5,1.5)和(5,-1.5),试写出由原图形得到新图形的平移的方向及距离.
B
例题
2
例题
1 1
例题
连线平行于坐标轴的点的特点
已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为_______________________.
(-1,-2)或(-1,6)
连线平行于坐标轴的点的特点
已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为_______________________.
(3,2)或(-5,2)
总结
这节课我们学会了什么?
点平移的坐标变化规律
点(x,y)
上移
a
下移
a
右移a
左移a
(x,y+a)
(x,y-a)
(x-a,y)
(x+a,y)
总结
图形上点的坐标变化与图形移动的关系
横坐标都加a
横坐标都减a
纵坐标都加a
纵坐标都减a
图形向右平移a
图形向左平移a
图形向上平移a
图形向下平移a
这节课我们学会了什么?
复习巩固
1.如图,三辆汽车P,Q,R保持编队行驶,分别写出它们的坐标,当汽车P行驶到P'位置时,汽车Q,R行驶到了什么位置?分别写出这三辆汽车新位置的坐标.
复习巩固
2.如图,机械手要将一个エ件从图中A处移动到B处,但是这个工件不能碰到图中的红色障碍,试用坐标写出一条机械手在移动中可能要走过的路线
复习巩固
3.如图,长方形ABCD四个顶点分别是A(-3,2),B(-3,-2),C(3,-2),D(3,2).将长方形向左平移2个单位长度,各个顶点的坐标变为什么?将它向上平移3个单位长度呢?分别画出平移后的图形
复习巩固
4.选择题.如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是(? ? ? ? ).?
(A)(2,2),(3,4),(1,7)?
(B)(-2,2),(4,3),(1,7)
(C)(-2,2),(3,4),(1,7)?
(D)(2,-2),(3,3),(1,7)
复习巩固
5.如图,这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示教学楼、图书馆、校门、实验楼、国旗杆的位置.类似地,你能用坐标表示你自己学校各主要建筑物的位置吗?
复习巩固
6.如图,在一次活动中,位于A处的1班准备前往相距5km的B处与2班会合,如何用方向和距离描述2班相对于1班的位置?反过来,如何用方向和距离描述1班相对于2班的位置?
综合运用
7.制作动画片时,经常要用到图形的平移.如图,小鸭子从A到B再到C,到D,这几个过程中,分别进行了怎样的平移?
综合运用
8.如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1.求A1,B1,C1的坐标
综合运用
9.如图,三角形AOB中,A,B两点的坐标分别为(2,4),(6,2),求三角形AOB的面积.(提示:三角形AOB的面积可以看作一个长方形的面积减去一些小三角形的面积.)
综合运用
综合运用
11.如图,三角形COB是由三角形AOB经过某种变換后得到的图形,观察点A与点C的坐标之间的关系.三角形AOB中任意一点M的坐标为(x,y),点M经过这种变换后得到点N,点N的坐标是什么?
综合运用
12.如图,这是一个利用平面直角坐标系画出的某动物园的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,并且猴山和狮虎山的坐标分别是(2,1)和(8,2).你能在此图上标出熊猫馆(6,6)的位置吗?
复习巩固
1.指出下列各点的横坐标和纵坐标,并指出各点所在的象限
A(2,3),B(一2,3),C(-2,-3),D(2,-3).
复习巩固
2.如图,写出八边形各顶点的坐标.
复习巩固
3.在同一平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(2,0),(4,0),(2,2);
(2)(0,2),(0,4),(-2,2);?
(3)(-4,0),(-2,-2),(-2,0);?
(4)(0,-2)、(2,-2),(0,-4).?
观察所得的图形,你觉得它像什么?
复习巩固
4.图中标明了李明家附近的一些地方.
(1)写出书店和邮局的坐标.
(2)某星期日早晨,李明同学从家里出发,沿(-100,200),(100,0),(200,100),(200,-200),(-100,-200),(0,-100)的路线转了一下,又回到家里,写出他路上经过的地方.
(3)连接他在(2)中经过的地点,你能得到什么图形?
复习巩固
5.如图,红色图形可以由蓝色图形经过怎样的平移得到?对应点的坐标有什么变化?
综合运用
6.(1)坐标(x,3)中的x取-3,-2,-1,0,1,2,3所表示的点是否在一条直线上?这条直线与、x轴有什么关系?
(2)坐标(3,y)中的y取-3,-2,-1,0,1,2,3所表示的点是否在一条直线上?这条直线与x轴有什么关系?
综合运用
7.图中显示了10名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h).?
(1)用有序数对表示图中各点.?
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?
综合运用
8.某村过去是一个缺水的村庄,由于兴修水利,现在家家户户都用上了自来水.据村委会主任徐伯伯讲,以前全村400多户人家只有五ロ水井:第一ロ在村委会的院子里,第二口在村委会北偏东30°方向2000m处,第三ロ在村委会正西方向1500m处,第四ロ在村委会东南方向1000m处,第五ロ在村委会正南方向900m处,请你根据徐伯伯的话,和同学们一起讨论,画图表示这个村庄五口水井的位置.
综合运用
拓广探索
10.建立平面直角坐标系,并描出下列各点:
A(1,1),B(5,1),C(3,3),D(-3,3),E(1,-2),F(1,4),G(3,2) ,H(3,-2),I(-1,-1),J(-1,1) .
连接AB,CD,EF,GH,IJ,找出它们中点的坐标,将上述中点的横坐标和纵坐标分别与对应线段的两个端点的横坐标和纵坐标进行比较,你发现它们之间有什么关系?写出你的发现,并与其他同学进行交流.
综合运用
11.如图,三角形PQR是三角形ABC经过某种变換后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系.三角形ABC中任意一点M的坐标为(x,y),点M经过这种变换后得到点N,点N的坐标是什么?
用坐标表示平移
掌握点或图形的平移引起点的坐标的变化规律.??
会根据图形上点的坐标的某种变化,得出图形进行了怎样的平移.
教学目标
教学重点
教学难点
在平面直角坐标系中,图形平移变化中坐标的变化规律.??
图形平移与其坐标变化之间的关系.
在平面直角坐标系中,探究点的坐标的某种变化引起的图形平移.
知识回顾
1、平移的定义
在平面内,将一个图形沿____________移动一定的距离,这样的图形运动称为平移.
2、平移的性质
(1)平移不改变图形的_____________, 只改变形图形的______.
(2)经过平移后,对应点所连的线段 _____________.
某个方向
形状和大小
位置
平行且相等
探究
点的平移
(-2,-3)
(-2,-3)
(-2,-3)
(-2,-3)
(3,-3)
(-4,-3)
(-2,3)
(-2,-7)
如图,将点A(-2, -3)向右平移5个单位长度,得到点A1,在图上标出这个点,并写出它的坐标.
把点A向左平移2个单位呢?
把点A向上平移6个单位呢?
把点A向下平移4个单位呢?
右移5个单位
横坐标+5
左移2个单位
横坐标-2
上移6个单位
纵坐标+6
下移4个单位
纵坐标-4
平移前后的坐标有什么关系?
归纳
点(x,y)
左右平移a个单位长度
横变纵不变
右加
(x+a,y)
左减
(x-a,y)
上下平移b个单位长度
纵变横不变
上加
下减
(x,y+b)
(x,y-b)
点(x,y)
例题
在平面直角坐标系中,有一点(1,3),要使它平移到点(-2,-2),应怎样平移?说出平移的路线.
先向下平移5个单位长度,
再向左平移3个单位长度.
先向左平移3个单位长度,
再向下平移5个单位长度.
1.将点A(3,2)向上平移2个单位长度,得到A’,则A’的坐标为______.??
2.将点A(3,2)向下平移3个单位长度,得到A’,则A’的坐标为________.?
3.将点A(3,2)向左平移4个单位长度,得到A’,则A’的坐标为________.?
4.将点A(3,2)向右平移2个单位长度,得到A’,则A’的坐标为______.
练习
(3,4)
(3,-1)
(-1,2)
(5,2)
(1)将点A(0,-8)向上平移2个单位长度,得到A’,则A’的坐标为___________.
练习
(2)将点A(2,-1)向左平移4个单位长度,得到A’,则A’的坐标为___________.
(0,-6)
(-2,-1)
练习
1、点P(2,-1)向左平移3个单位长度得点Q的坐标为________.
2、点P(2,-1)向上平移2个单位长度得点Q的坐标为________.
3、点P(2,-1)向右平移3个单位长度,再向下平移2个单位长度得点Q的坐标为___________.
(-1,-1 )
( 2,1 )
( 5,-3 )
练习
已知点A(3,2),将点A先向右平移2个单位长度,再向上平移5个单位长度,得到A′,则A′的坐标为________.
(5,7)
练习
将点P(0,-2)向左平移2个单位,再向上平移4个单位得点Q(x,y),则xy=_____.
-4
1.把点M(1,2)平移后得到点N(1,-2) ,则平移的过程是:_________________.
2.把点M(-3,1)平移后得到点N(-1,4),则平移的过程是:_______________________________________________________.
向下平移4个单位
向右平移2个单位,再向上平移3个单位
或:向上平移3个单位,再向右平移2个单位
练习——求平移量
练习——反求
将点P(m,1)向右平移5个单位长度,得到点Q(3,1),则点P坐标为___________.
(-2,1)
练习——反求
将点M(a,b)向左平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,-6),则a=____,b=____.
3
-3
练习
将点P(m+2,2m+4)向右平移1个单位得到P’,且P’在y轴上,那么P’坐标是(? ? ? ? ) .
A.(-2,0)??
B.(0,-2)?
C.(1,0)?
D.(0,1)
B
探究
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.
(1)点E,F,G,H的坐标分别是什么?
E(6,-3),F(6,-4),G(7,-4),H(7,-3).
探究
如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E,F,G,H.??
(2)如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
归纳
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到.
对一个图形进行平移,这个图形上所有点的坐标都要发生相应的变化;反过来,从图示上的点的坐标的某种变化,我们也可以看出对这个图形进行了怎样的平移.
例题
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将三角形ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,点A1,B1,C1坐标分别是什么?并画出相应的三角形A1B1C1?.
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
例题
三角形A1B1C1与三角形ABC的大小、形状和位置上有什么关系?
大小和形状不变,
思考
△ A1B1C1可以看做△ABC向左平移6个单位长度得到的.
例题
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(2)将三角形ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,点A2,B2,C2坐标分别是什么?并画出相应的三角形A2B2C2.
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
例题
三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
大小和形状不变,
思考
△ A2B2C2可以看做△ABC向下平移5个单位长度得到的.
例题
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
如图,将三角形ABC三个顶点的横坐标都减去 6,同时纵坐标减去5,又能得到什么结论?
如图,三角形ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
例题
三角形A2B2C2与三角形ABC的大小、形状和位置上有什么关系?
大小和形状不变,
思考
可以发现所得三角形可以由三角形ABC向左平移6个单位长度,再向下平移了5个单位长度.?
归纳总结
图形上点的坐标变化与图形移动的关系
横坐标都加a
横坐标都减a
纵坐标都加a
纵坐标都减a
图形向右平移a
图形向左平移a
图形向上平移a
图形向下平移a
练习
将平行四边形ABCD向左平移2个单位长度,向上平移3个单位长度,可以得到平行四边形A'B'C'D',画出平移后的图形,并指出其各个顶点的坐标.
各个顶点的坐标是
A'(-3,1);
B'(1,1);
C'(2,4);
D'(-2,4).
练习
已知△ABC在平面直角坐标系中的位置如图所示,将△ABC向下平移5个单位,再向左平移2个单位,则平移后C点的坐标是
(? ? ?).?
(A)(5,-2)
(B)(1,-2)
(C)(2,-1)
(D)(2,-2)
B
练习
如图,△ABC的三个顶点的坐标分别是A(-4,-1),B(-5,-4),C(-1,-3),将这三点的横坐标加6,同时纵坐标加4,分别得到点A',B',C',依次连接A',B',C'各点,说明△A'B'C'可以由△ABC沿坐标轴方向平移得到.
补充题
已知图形上一点的坐标变化
平移一个图形时,图形上所有点的坐标变化_______ ,
所以已知一点的坐标变化, 就能得到其他所有点的坐标变化.
相同
已知图形上一点的坐标变化
如图,已知铅笔尖平移前后的坐标分别为(5,1.5)和(5,-1.5),试写出由原图形得到新图形的平移的方向及距离.
B
例题
2
例题
1 1
例题
连线平行于坐标轴的点的特点
已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为_______________________.
(-1,-2)或(-1,6)
连线平行于坐标轴的点的特点
已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为_______________________.
(3,2)或(-5,2)
总结
这节课我们学会了什么?
点平移的坐标变化规律
点(x,y)
上移
a
下移
a
右移a
左移a
(x,y+a)
(x,y-a)
(x-a,y)
(x+a,y)
总结
图形上点的坐标变化与图形移动的关系
横坐标都加a
横坐标都减a
纵坐标都加a
纵坐标都减a
图形向右平移a
图形向左平移a
图形向上平移a
图形向下平移a
这节课我们学会了什么?
复习巩固
1.如图,三辆汽车P,Q,R保持编队行驶,分别写出它们的坐标,当汽车P行驶到P'位置时,汽车Q,R行驶到了什么位置?分别写出这三辆汽车新位置的坐标.
复习巩固
2.如图,机械手要将一个エ件从图中A处移动到B处,但是这个工件不能碰到图中的红色障碍,试用坐标写出一条机械手在移动中可能要走过的路线
复习巩固
3.如图,长方形ABCD四个顶点分别是A(-3,2),B(-3,-2),C(3,-2),D(3,2).将长方形向左平移2个单位长度,各个顶点的坐标变为什么?将它向上平移3个单位长度呢?分别画出平移后的图形
复习巩固
4.选择题.如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,则平移后三个顶点的坐标是(? ? ? ? ).?
(A)(2,2),(3,4),(1,7)?
(B)(-2,2),(4,3),(1,7)
(C)(-2,2),(3,4),(1,7)?
(D)(2,-2),(3,3),(1,7)
复习巩固
5.如图,这是一所学校的平面示意图,建立适当的平面直角坐标系,并用坐标表示教学楼、图书馆、校门、实验楼、国旗杆的位置.类似地,你能用坐标表示你自己学校各主要建筑物的位置吗?
复习巩固
6.如图,在一次活动中,位于A处的1班准备前往相距5km的B处与2班会合,如何用方向和距离描述2班相对于1班的位置?反过来,如何用方向和距离描述1班相对于2班的位置?
综合运用
7.制作动画片时,经常要用到图形的平移.如图,小鸭子从A到B再到C,到D,这几个过程中,分别进行了怎样的平移?
综合运用
8.如图,三角形ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1.求A1,B1,C1的坐标
综合运用
9.如图,三角形AOB中,A,B两点的坐标分别为(2,4),(6,2),求三角形AOB的面积.(提示:三角形AOB的面积可以看作一个长方形的面积减去一些小三角形的面积.)
综合运用
综合运用
11.如图,三角形COB是由三角形AOB经过某种变換后得到的图形,观察点A与点C的坐标之间的关系.三角形AOB中任意一点M的坐标为(x,y),点M经过这种变换后得到点N,点N的坐标是什么?
综合运用
12.如图,这是一个利用平面直角坐标系画出的某动物园的示意图,如果这个坐标系分别以正东、正北方向为x轴、y轴的正方向,并且猴山和狮虎山的坐标分别是(2,1)和(8,2).你能在此图上标出熊猫馆(6,6)的位置吗?
复习巩固
1.指出下列各点的横坐标和纵坐标,并指出各点所在的象限
A(2,3),B(一2,3),C(-2,-3),D(2,-3).
复习巩固
2.如图,写出八边形各顶点的坐标.
复习巩固
3.在同一平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(2,0),(4,0),(2,2);
(2)(0,2),(0,4),(-2,2);?
(3)(-4,0),(-2,-2),(-2,0);?
(4)(0,-2)、(2,-2),(0,-4).?
观察所得的图形,你觉得它像什么?
复习巩固
4.图中标明了李明家附近的一些地方.
(1)写出书店和邮局的坐标.
(2)某星期日早晨,李明同学从家里出发,沿(-100,200),(100,0),(200,100),(200,-200),(-100,-200),(0,-100)的路线转了一下,又回到家里,写出他路上经过的地方.
(3)连接他在(2)中经过的地点,你能得到什么图形?
复习巩固
5.如图,红色图形可以由蓝色图形经过怎样的平移得到?对应点的坐标有什么变化?
综合运用
6.(1)坐标(x,3)中的x取-3,-2,-1,0,1,2,3所表示的点是否在一条直线上?这条直线与、x轴有什么关系?
(2)坐标(3,y)中的y取-3,-2,-1,0,1,2,3所表示的点是否在一条直线上?这条直线与x轴有什么关系?
综合运用
7.图中显示了10名学生平均每周用于阅读课外书的时间和用于看电视的时间(单位:h).?
(1)用有序数对表示图中各点.?
(2)图中有一个点位于方格的对角线上,这表示什么意思?
(3)图中方格纸的对角线的左上方的点有什么共同的特点?它右下方的点呢?
(4)估计一下你每周用于阅读课外书的时间和用于看电视的时间,在图上描出来,这个点位于什么位置?
综合运用
8.某村过去是一个缺水的村庄,由于兴修水利,现在家家户户都用上了自来水.据村委会主任徐伯伯讲,以前全村400多户人家只有五ロ水井:第一ロ在村委会的院子里,第二口在村委会北偏东30°方向2000m处,第三ロ在村委会正西方向1500m处,第四ロ在村委会东南方向1000m处,第五ロ在村委会正南方向900m处,请你根据徐伯伯的话,和同学们一起讨论,画图表示这个村庄五口水井的位置.
综合运用
拓广探索
10.建立平面直角坐标系,并描出下列各点:
A(1,1),B(5,1),C(3,3),D(-3,3),E(1,-2),F(1,4),G(3,2) ,H(3,-2),I(-1,-1),J(-1,1) .
连接AB,CD,EF,GH,IJ,找出它们中点的坐标,将上述中点的横坐标和纵坐标分别与对应线段的两个端点的横坐标和纵坐标进行比较,你发现它们之间有什么关系?写出你的发现,并与其他同学进行交流.
综合运用
11.如图,三角形PQR是三角形ABC经过某种变換后得到的图形,分别写出点A与点P,点B与点Q,点C与点R的坐标,并观察它们之间的关系.三角形ABC中任意一点M的坐标为(x,y),点M经过这种变换后得到点N,点N的坐标是什么?
