苏教版高二数学选修2-3 1.1两个基本计数原理(2)(共18张PPT)
文档属性
| 名称 | 苏教版高二数学选修2-3 1.1两个基本计数原理(2)(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
两个基本计数原理(2)
南京师范大学第二附属高级中学
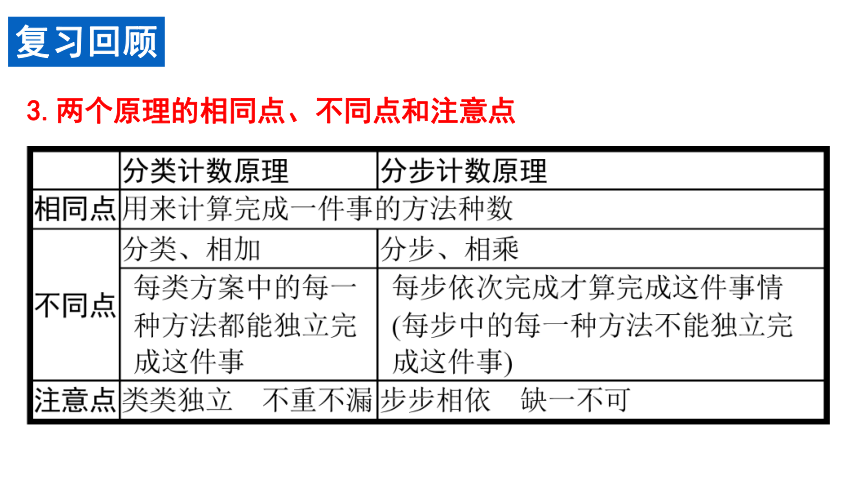
复习回顾
1.分类计数原理(加法原理) :
m1+m2+…+mn
完成一件事,有 类方式,在第1类方式中有 种不同的方法,在
第2类方式中有 种不同的方法,......,在第 类方式中有 种
不同的方法,那么完成这件事共有______________种不同的方法
2.分步计数原理(乘法原理) :
完成一件事,需要分成 个步骤,做第1步有 种不同的方法,做
第2步有 种不同的方法,......,做第 步有 种不同的方法,
那么完成这件事共有_______________种不同的方法
m1×m2×…×mn
3.两个原理的相同点、不同点和注意点
复习回顾
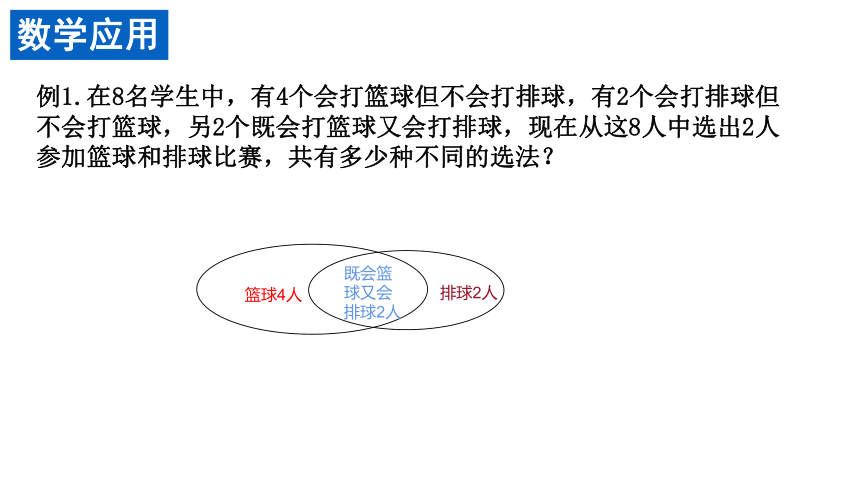
数学应用
篮球4人
排球2人
既会篮
球又会
排球2人
例1.在8名学生中,有4个会打篮球但不会打排球,有2个会打排球但
不会打篮球,另2个既会打篮球又会打排球,现在从这8人中选出2人
参加篮球和排球比赛,共有多少种不同的选法?
分析.
完成选出2人参加篮球和排球比赛,可分为2类:
第1类从只会打篮球的4人中选1人参加篮球比赛,这时剩余的7人
中有4人会打排球从中选1人参加排球比赛,有 种选法
第2类从既会打篮球又会打排球的2人中选1人参加篮球比赛,
这时剩余的7人中有3人会打排球从中选1人参加排球比赛,有
种选法
根据分类计数原理共有 种
数学应用
篮球4人
排球2人
既会篮
球又会
排球2人
例1.在8名学生中,有4个会打篮球但不会打排球,有2个会打排球但
不会打篮球,另2个既会打篮球又会打排球,现在从这8人中选出2人
参加篮球和排球比赛,共有多少种不同的选法?
分析.
完成选出2人参加篮球和排球比赛,也可分为2类:
第1类从只会打排球的2人中选1人参加排球比赛,这时剩余的7人
中有6人会打篮球从中选1人参加篮球比赛,有 种选法
第2类从既会打篮球又会打排球的的2人中选1人参加排球比赛,
这时剩余的7人中有5人会打篮球从中选1人参加篮球比赛,有
种选法
根据分类计数原理共有 种
方法总结
先确定分类的标准(分类标准可能有多个,但不论是以哪一个为标准,
都遵循“标准要明确,不重不漏”的原则,且完成这件事情的任何一种
方法必须属于某一类)
定好类数,再逐类计算(计算每类种数时有时用到分步计数原理)
最后根据分类计数原理得出结果
利用分类计数原理解决问题时应注意:
例2.用0、1、2、3、4五个数字可以组成多少个无重复数字的4位数?
完成组成无重复的4位数这件事,可以分4个步骤:
分析:
第一步 定千位,有4种选法
第二步 定百位,有4种选法
第三步 定十位,有3种选法
第四步 定个位,有2种选法
根据分步计数原理可以组成无重复数字的4位数共有 种
千 百 十 个
变式:用0、1、2、3、4五个数字可以组成多少个无重复数字的
4位数的奇数?
分析:
完成组成无重复数字的4位数的奇数这件事,可以分四个步骤:
第一步 定个位只能从1、3中任取一个有2种不同方法
千 百 十 个
第二步 定千位有3种不同方法
第三步定百位有3种不同方法
第四步定十位有2种不同方法
根据分步计数原理共有 种
利用分步计数原理解决问题时应注意:
方法总结
(1)要按事件发生的过程合理分步,即分步是有先后顺序的,以元素(或位置)为主体的计数问题,通常先考虑特殊元素(或位置),再考虑其他元素(或位置);
(2)对完成每一步的不同方法种数要根据条件准确确定
例3. 有4种不同颜色给如图所示的地图涂色,要求相邻两块涂
不同的颜色,共有多少种不同的涂法?
分析:
完成给地图涂色这件事,可分为4个步骤:
第一步填涂A有4种不同颜色
A
B
C
D
第二步填涂B除A处所用过的颜色外还有3种不同颜色可选
第三步填涂C除A,B用过的2种颜色外还有2种不同颜色可选
第四步填涂D 除B,C用过的2种颜色外还有2种颜色可选
根据分步计数原理知有 种
思考:如果按A→B→D→C的次序填涂,怎样完成这件事?
完成这件事可分为2类:
A
B
C
D
第1类当D和A同色有
第2类当D和A不同色
共有
变式:有4种不同颜色给如图所示的地图涂色,要求相邻两块
涂不同的颜色,共有多少种不同的涂法?
分析:
B
D
E
A
C
完成这件事可以分2类
第1类D和A同色有 种
第2类D和A不同色有 种
共有 种
方法总结
对于两个计数原理的综合应用问题,要分清是先分类再分
步,还是先分步再分类。分类时要设计好标准,设计好分
类方案,防止重复和遗漏;分步时要注意步与步之间的连
续性,同时应合理设计步骤的顺序,使各步互不干扰.
当堂训练
1.用1,2,3,可以写出______个小于1000的正整数
2.现有4种不同的颜色对如图的4个部分进行涂色,要求有公
共边界的两边不能用1种颜色,则不同的涂
色方法有____种
B
C
D
A
39
48
回顾总结
本节课和同学们通过研究多面手,组数,涂色3类问题,来体会两
个原理的具体运用,首先我们明确要完成一件什么事,通过对问题
的分析合理地选择分类或分步计数原理来解决问题
谢谢聆听
两个基本计数原理(2)
南京师范大学第二附属高级中学
复习回顾
1.分类计数原理(加法原理) :
m1+m2+…+mn
完成一件事,有 类方式,在第1类方式中有 种不同的方法,在
第2类方式中有 种不同的方法,......,在第 类方式中有 种
不同的方法,那么完成这件事共有______________种不同的方法
2.分步计数原理(乘法原理) :
完成一件事,需要分成 个步骤,做第1步有 种不同的方法,做
第2步有 种不同的方法,......,做第 步有 种不同的方法,
那么完成这件事共有_______________种不同的方法
m1×m2×…×mn
3.两个原理的相同点、不同点和注意点
复习回顾
数学应用
篮球4人
排球2人
既会篮
球又会
排球2人
例1.在8名学生中,有4个会打篮球但不会打排球,有2个会打排球但
不会打篮球,另2个既会打篮球又会打排球,现在从这8人中选出2人
参加篮球和排球比赛,共有多少种不同的选法?
分析.
完成选出2人参加篮球和排球比赛,可分为2类:
第1类从只会打篮球的4人中选1人参加篮球比赛,这时剩余的7人
中有4人会打排球从中选1人参加排球比赛,有 种选法
第2类从既会打篮球又会打排球的2人中选1人参加篮球比赛,
这时剩余的7人中有3人会打排球从中选1人参加排球比赛,有
种选法
根据分类计数原理共有 种
数学应用
篮球4人
排球2人
既会篮
球又会
排球2人
例1.在8名学生中,有4个会打篮球但不会打排球,有2个会打排球但
不会打篮球,另2个既会打篮球又会打排球,现在从这8人中选出2人
参加篮球和排球比赛,共有多少种不同的选法?
分析.
完成选出2人参加篮球和排球比赛,也可分为2类:
第1类从只会打排球的2人中选1人参加排球比赛,这时剩余的7人
中有6人会打篮球从中选1人参加篮球比赛,有 种选法
第2类从既会打篮球又会打排球的的2人中选1人参加排球比赛,
这时剩余的7人中有5人会打篮球从中选1人参加篮球比赛,有
种选法
根据分类计数原理共有 种
方法总结
先确定分类的标准(分类标准可能有多个,但不论是以哪一个为标准,
都遵循“标准要明确,不重不漏”的原则,且完成这件事情的任何一种
方法必须属于某一类)
定好类数,再逐类计算(计算每类种数时有时用到分步计数原理)
最后根据分类计数原理得出结果
利用分类计数原理解决问题时应注意:
例2.用0、1、2、3、4五个数字可以组成多少个无重复数字的4位数?
完成组成无重复的4位数这件事,可以分4个步骤:
分析:
第一步 定千位,有4种选法
第二步 定百位,有4种选法
第三步 定十位,有3种选法
第四步 定个位,有2种选法
根据分步计数原理可以组成无重复数字的4位数共有 种
千 百 十 个
变式:用0、1、2、3、4五个数字可以组成多少个无重复数字的
4位数的奇数?
分析:
完成组成无重复数字的4位数的奇数这件事,可以分四个步骤:
第一步 定个位只能从1、3中任取一个有2种不同方法
千 百 十 个
第二步 定千位有3种不同方法
第三步定百位有3种不同方法
第四步定十位有2种不同方法
根据分步计数原理共有 种
利用分步计数原理解决问题时应注意:
方法总结
(1)要按事件发生的过程合理分步,即分步是有先后顺序的,以元素(或位置)为主体的计数问题,通常先考虑特殊元素(或位置),再考虑其他元素(或位置);
(2)对完成每一步的不同方法种数要根据条件准确确定
例3. 有4种不同颜色给如图所示的地图涂色,要求相邻两块涂
不同的颜色,共有多少种不同的涂法?
分析:
完成给地图涂色这件事,可分为4个步骤:
第一步填涂A有4种不同颜色
A
B
C
D
第二步填涂B除A处所用过的颜色外还有3种不同颜色可选
第三步填涂C除A,B用过的2种颜色外还有2种不同颜色可选
第四步填涂D 除B,C用过的2种颜色外还有2种颜色可选
根据分步计数原理知有 种
思考:如果按A→B→D→C的次序填涂,怎样完成这件事?
完成这件事可分为2类:
A
B
C
D
第1类当D和A同色有
第2类当D和A不同色
共有
变式:有4种不同颜色给如图所示的地图涂色,要求相邻两块
涂不同的颜色,共有多少种不同的涂法?
分析:
B
D
E
A
C
完成这件事可以分2类
第1类D和A同色有 种
第2类D和A不同色有 种
共有 种
方法总结
对于两个计数原理的综合应用问题,要分清是先分类再分
步,还是先分步再分类。分类时要设计好标准,设计好分
类方案,防止重复和遗漏;分步时要注意步与步之间的连
续性,同时应合理设计步骤的顺序,使各步互不干扰.
当堂训练
1.用1,2,3,可以写出______个小于1000的正整数
2.现有4种不同的颜色对如图的4个部分进行涂色,要求有公
共边界的两边不能用1种颜色,则不同的涂
色方法有____种
B
C
D
A
39
48
回顾总结
本节课和同学们通过研究多面手,组数,涂色3类问题,来体会两
个原理的具体运用,首先我们明确要完成一件什么事,通过对问题
的分析合理地选择分类或分步计数原理来解决问题
谢谢聆听
