五年级下册数学课件 探究和的奇偶性(共13张ppt)
文档属性
| 名称 | 五年级下册数学课件 探究和的奇偶性(共13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 365.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 19:52:24 | ||
图片预览




文档简介
(共12张PPT)
因数与倍数
质数和合数
探究和的奇偶性
一、复习回顾
23 47 71 97
30 52 33 85 98
质数:
1.判断下列各数,哪些是质数?哪些是合数?
23 30 47 52 33 71 85 97 98
合数:
是2的倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇数。
2.怎样判断一个数是奇数还是偶数呢?
二、探究新知
奇数与偶数的和是奇数还是偶数?
奇数与奇数的和是奇数还是偶数?
偶数与偶数的和呢?
奇数+偶数=
奇数?
偶数?
奇数+奇数=
奇数?
偶数?
偶数+偶数=
奇数?
偶数?
二、探究新知
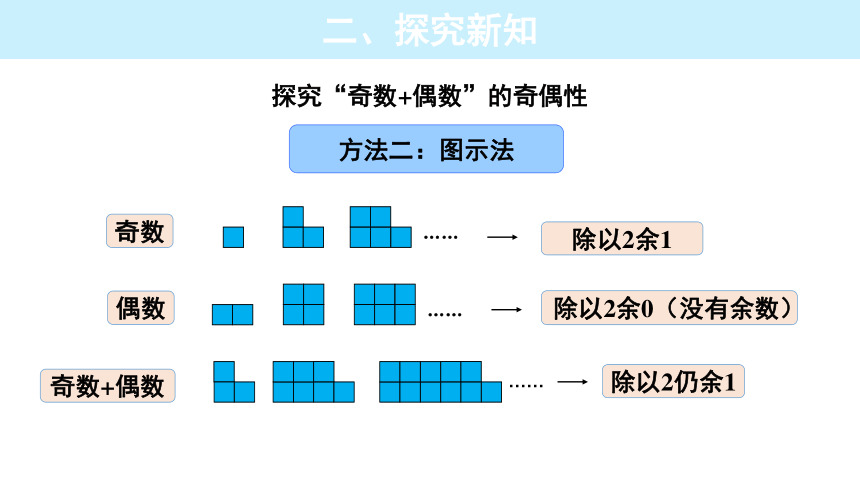
探究“奇数+偶数”的奇偶性
方法一:通过举例推断
奇数:5, 7, 9, 11,… 偶数:8,12,20,24,…
5+8=13,7+12=19,9+20=29,11+24=35
……
奇数+偶数=奇数
二、探究新知
探究“奇数+偶数”的奇偶性
方法二:图示法
奇数+偶数
偶数
奇数
……
……
除以2余1
除以2余0(没有余数)
……
除以2仍余1
二、探究新知
偶数
奇数
5,7,9,11,…
8,12,20,24,…
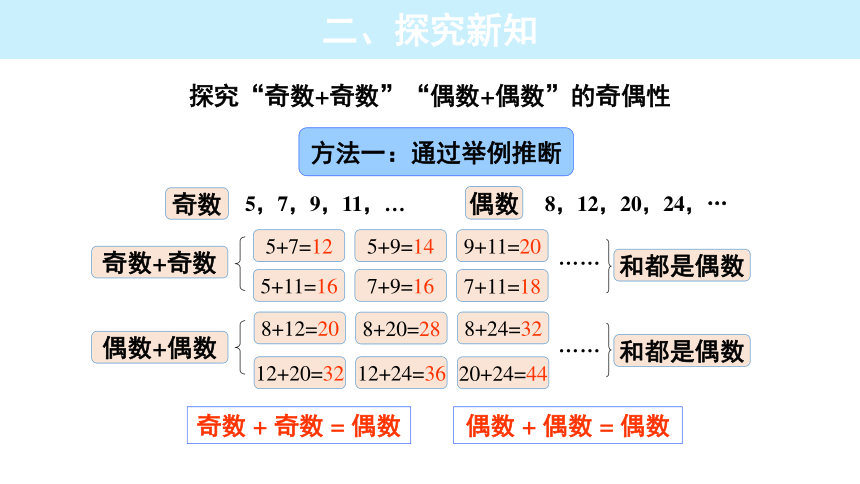
奇数+奇数
5+7=12
5+11=16
5+9=14
7+9=16
和都是偶数
7+11=18
9+11=20
……
偶数+偶数
8+12=20
12+20=32
8+20=28
12+24=36
和都是偶数
20+24=44
8+24=32
……
偶数 + 偶数 = 偶数
奇数 + 奇数 = 偶数
探究“奇数+奇数”“偶数+偶数”的奇偶性
方法一:通过举例推断
二、探究新知
探究“奇数+奇数”“偶数+偶数”的奇偶性
方法二:图示法
奇数+奇数
偶数
奇数
……
……
除以2余1
除以2余0
……
除以2余0
除以2余0
偶数+偶数
……
偶数 + 偶数 = 偶数
奇数 + 奇数 = 偶数
二、探究新知
奇数 + 奇数 = 偶数
奇数 + 偶数 = 奇数
偶数 + 偶数 = 偶数
319+534=853
123+222=345
985+300=1285
620+312=932
434+318=752
246+132=378
537+319=856
533+317=850
321+319=640
三、巩固练习
1.30名学生要分成甲、乙两队。如果甲队人数为奇数,乙队人数为奇数还是偶数?如果甲队人数为偶数呢?
如果甲队人数为奇数,乙队人数为奇数
如果甲队人数为偶数,乙队人数为偶数
三、巩固练习
2.用“偶数”和“奇数”填空:
偶数+( )=偶数 偶数×偶数=( )
( )+奇数=奇数 奇数×奇数=( )
奇数+( )=偶数 奇数×( )=偶数
偶数
偶数
偶数
奇数
奇数
偶数
三、巩固练习
偶数
3.1+2+3+4+5+…+119+120的结果是奇数还是偶数?
四、课堂小结
偶数+偶数=偶数
奇数+奇数=偶数
偶数+奇数=奇数
因数与倍数
质数和合数
探究和的奇偶性
一、复习回顾
23 47 71 97
30 52 33 85 98
质数:
1.判断下列各数,哪些是质数?哪些是合数?
23 30 47 52 33 71 85 97 98
合数:
是2的倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇数。
2.怎样判断一个数是奇数还是偶数呢?
二、探究新知
奇数与偶数的和是奇数还是偶数?
奇数与奇数的和是奇数还是偶数?
偶数与偶数的和呢?
奇数+偶数=
奇数?
偶数?
奇数+奇数=
奇数?
偶数?
偶数+偶数=
奇数?
偶数?
二、探究新知
探究“奇数+偶数”的奇偶性
方法一:通过举例推断
奇数:5, 7, 9, 11,… 偶数:8,12,20,24,…
5+8=13,7+12=19,9+20=29,11+24=35
……
奇数+偶数=奇数
二、探究新知
探究“奇数+偶数”的奇偶性
方法二:图示法
奇数+偶数
偶数
奇数
……
……
除以2余1
除以2余0(没有余数)
……
除以2仍余1
二、探究新知
偶数
奇数
5,7,9,11,…
8,12,20,24,…
奇数+奇数
5+7=12
5+11=16
5+9=14
7+9=16
和都是偶数
7+11=18
9+11=20
……
偶数+偶数
8+12=20
12+20=32
8+20=28
12+24=36
和都是偶数
20+24=44
8+24=32
……
偶数 + 偶数 = 偶数
奇数 + 奇数 = 偶数
探究“奇数+奇数”“偶数+偶数”的奇偶性
方法一:通过举例推断
二、探究新知
探究“奇数+奇数”“偶数+偶数”的奇偶性
方法二:图示法
奇数+奇数
偶数
奇数
……
……
除以2余1
除以2余0
……
除以2余0
除以2余0
偶数+偶数
……
偶数 + 偶数 = 偶数
奇数 + 奇数 = 偶数
二、探究新知
奇数 + 奇数 = 偶数
奇数 + 偶数 = 奇数
偶数 + 偶数 = 偶数
319+534=853
123+222=345
985+300=1285
620+312=932
434+318=752
246+132=378
537+319=856
533+317=850
321+319=640
三、巩固练习
1.30名学生要分成甲、乙两队。如果甲队人数为奇数,乙队人数为奇数还是偶数?如果甲队人数为偶数呢?
如果甲队人数为奇数,乙队人数为奇数
如果甲队人数为偶数,乙队人数为偶数
三、巩固练习
2.用“偶数”和“奇数”填空:
偶数+( )=偶数 偶数×偶数=( )
( )+奇数=奇数 奇数×奇数=( )
奇数+( )=偶数 奇数×( )=偶数
偶数
偶数
偶数
奇数
奇数
偶数
三、巩固练习
偶数
3.1+2+3+4+5+…+119+120的结果是奇数还是偶数?
四、课堂小结
偶数+偶数=偶数
奇数+奇数=偶数
偶数+奇数=奇数
