4.4 一元一次不等式及其解法——解一元一次不等式 课件(17张PPT)
文档属性
| 名称 | 4.4 一元一次不等式及其解法——解一元一次不等式 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 251.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 11:09:45 | ||
图片预览



文档简介
课件17张PPT。解一元一次不等式复习1:(1)不等式两边加(或减)同一个 (或 ),不等号的 .
(2)不等式两边乘(或除以)同一个 ,不等号的 .
(3)不等式两边乘(或除以)同一个 ,不等号的方向 .方向不变正数方向不变负数改变1、不等式的基本性质2、已知:a<b
用“>”或“<”填空,
并说明理由
(1)a-3 b-3 (2)a/2 b/2
(3)-2a -2b (4)3a+1 3b+1
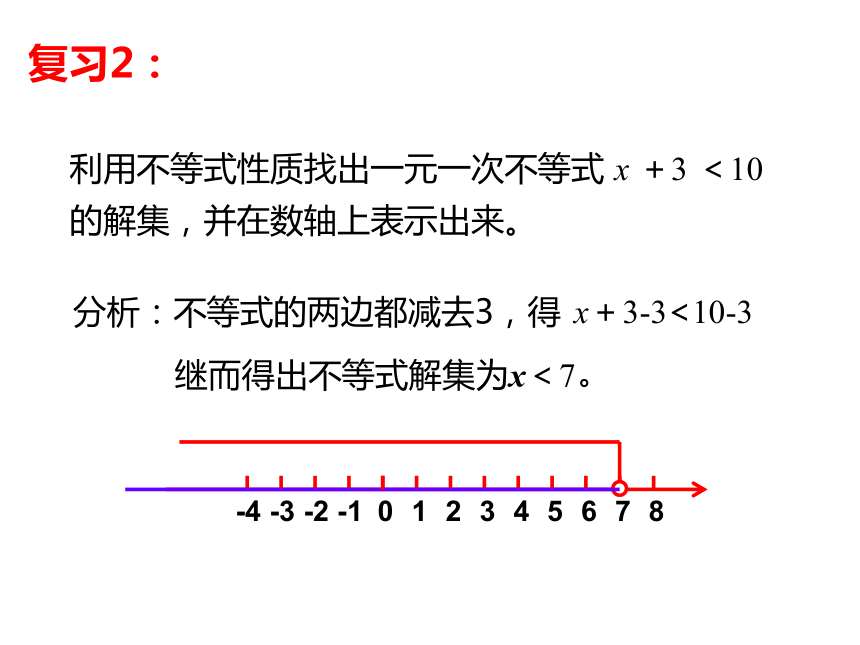
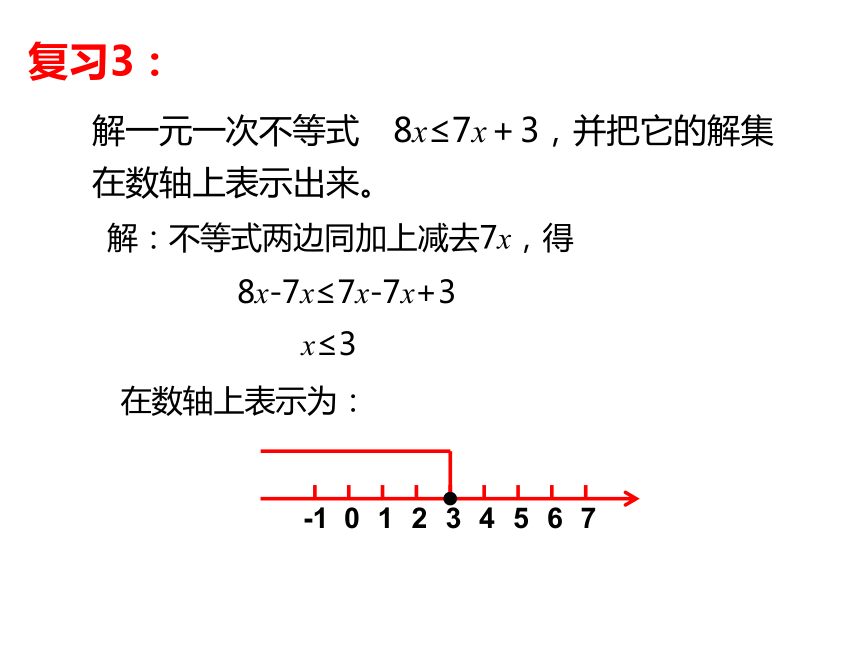
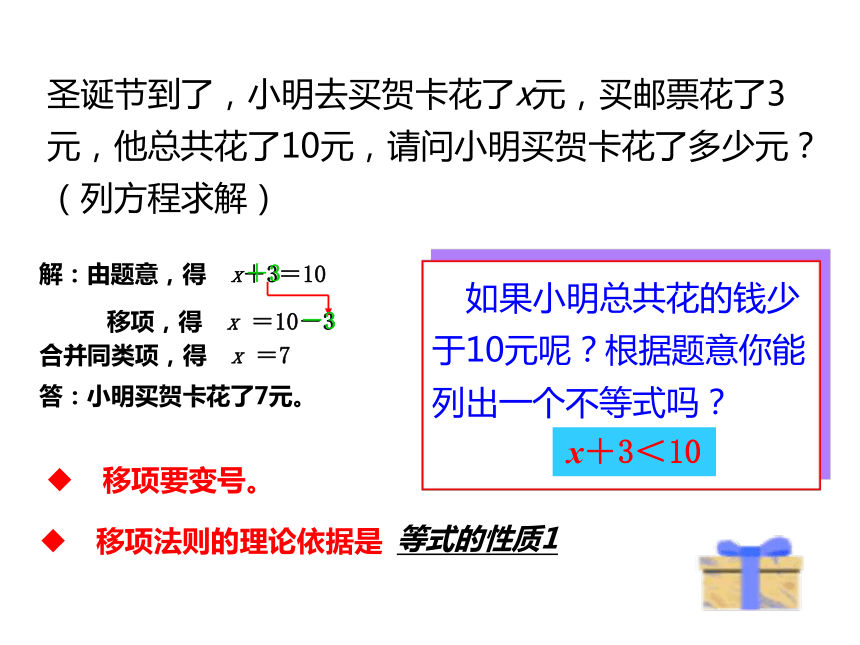
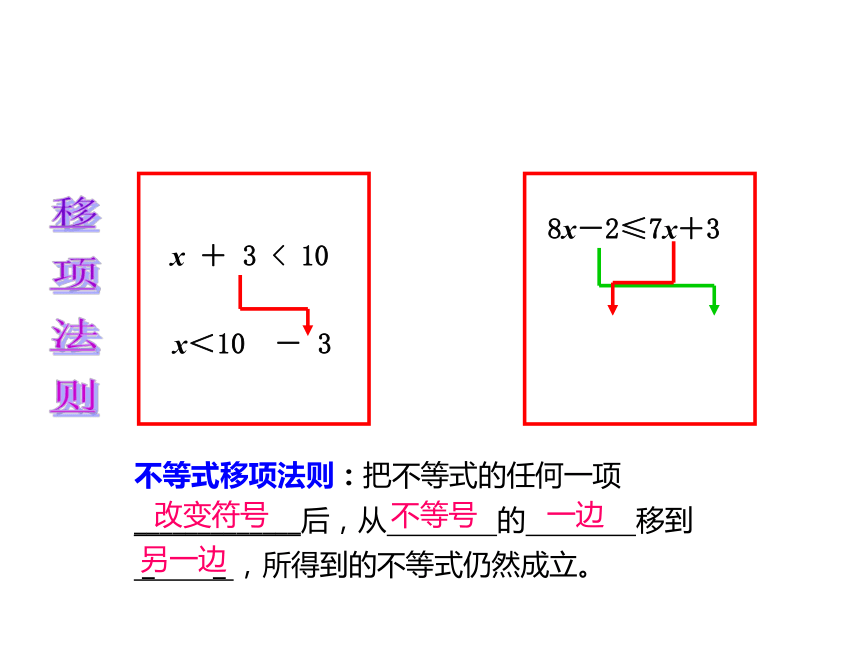
(5)a-b 0 (6)1-a 1-b<<<<>>分析:不等式的两边都减去3,得 x+3-3<10-3利用不等式性质找出一元一次不等式 x +3 <10的解集,并在数轴上表示出来。继而得出不等式解集为x<7。复习2:解:不等式两边同加上减去7x,得 8x-7x≤7x-7x+3x≤3在数轴上表示为:复习3:圣诞节到了,小明去买贺卡花了x元,买邮票花了3元,他总共花了10元,请问小明买贺卡花了多少元?(列方程求解)解:由题意,得 x+3=10移项,得 x =10-3 合并同类项,得 x =7答:小明买贺卡花了7元。 移项法则的理论依据是 如果小明总共花的钱少于10元呢?根据题意你能列出一个不等式吗?
移项要变号。等式的性质1x+3<10+3-3移
项
法
则不等式移项法则:把不等式的任何一项 _____________后,从 的 移到 _ _,所得到的不等式仍然成立。 改变符号不等号一边另一边填 空:解不等式:-2x+1>3-3x
解 : -2x+1 > 3 -3x
移项,得 -2x >3
合并同类项,得 >
+3x-1x2例1:解一元一次不等式 8x≤5x+3,并把它的解集在数轴上表示出来。 解:移项得:8x- 5x ≤+3 3x≤3在数轴上表示为:∴ 此不等式的解集为x≤1。 x≤1合并同类项得:系数化1得:练习:解不等式并在数轴上表示解集
1、5x-1≥5
2、3x<2x+1例2 解不等式
3(1-x)>2(1-2x)解:去括号,得 3-3x>2-4x移项,得 4x-3x>2-3合并同类项,得 x >-1∴ 原不等式的解集是 x>-1。例2 解不等式
3(1-x)>2(1-2x)例3:3(1+x)>2(1+2x)变
形解:去括号,得 3+3x>2+4x移项,得 3x - 4x > 2 - 3合并同类项,得 -x>-1系数化1,得 x<1 ∴ 原不等式的解集是 x<1。系数化为1:要注意不等号的两边同时除以的是一个正数还是负数,若是负数则不等号的方向改变。比一比,谁做得又快又好!练
习小
结解一元一次不等式的一般步骤为:去分母
去括号
移项
合并同类项
系数化为1
小
结不等式移项法则:把不等式的任何一项改变符号后,从不等式的一边移到另一边,所得到的不等式仍然成立。 系数化为1:要注意不等号的两边同时除以的是一个正数还是负数,若是负数则不等号的方向改变。1、求不等式3(x-3)-1≤2x+2的正整数解。思考2、x取什么值时,代数式 的值。
(1)大于0 (2)不小于想
一
想
(2)不等式两边乘(或除以)同一个 ,不等号的 .
(3)不等式两边乘(或除以)同一个 ,不等号的方向 .方向不变正数方向不变负数改变1、不等式的基本性质2、已知:a<b
用“>”或“<”填空,
并说明理由
(1)a-3 b-3 (2)a/2 b/2
(3)-2a -2b (4)3a+1 3b+1
(5)a-b 0 (6)1-a 1-b<<<<>>分析:不等式的两边都减去3,得 x+3-3<10-3利用不等式性质找出一元一次不等式 x +3 <10的解集,并在数轴上表示出来。继而得出不等式解集为x<7。复习2:解:不等式两边同加上减去7x,得 8x-7x≤7x-7x+3x≤3在数轴上表示为:复习3:圣诞节到了,小明去买贺卡花了x元,买邮票花了3元,他总共花了10元,请问小明买贺卡花了多少元?(列方程求解)解:由题意,得 x+3=10移项,得 x =10-3 合并同类项,得 x =7答:小明买贺卡花了7元。 移项法则的理论依据是 如果小明总共花的钱少于10元呢?根据题意你能列出一个不等式吗?
移项要变号。等式的性质1x+3<10+3-3移
项
法
则不等式移项法则:把不等式的任何一项 _____________后,从 的 移到 _ _,所得到的不等式仍然成立。 改变符号不等号一边另一边填 空:解不等式:-2x+1>3-3x
解 : -2x+1 > 3 -3x
移项,得 -2x >3
合并同类项,得 >
+3x-1x2例1:解一元一次不等式 8x≤5x+3,并把它的解集在数轴上表示出来。 解:移项得:8x- 5x ≤+3 3x≤3在数轴上表示为:∴ 此不等式的解集为x≤1。 x≤1合并同类项得:系数化1得:练习:解不等式并在数轴上表示解集
1、5x-1≥5
2、3x<2x+1例2 解不等式
3(1-x)>2(1-2x)解:去括号,得 3-3x>2-4x移项,得 4x-3x>2-3合并同类项,得 x >-1∴ 原不等式的解集是 x>-1。例2 解不等式
3(1-x)>2(1-2x)例3:3(1+x)>2(1+2x)变
形解:去括号,得 3+3x>2+4x移项,得 3x - 4x > 2 - 3合并同类项,得 -x>-1系数化1,得 x<1 ∴ 原不等式的解集是 x<1。系数化为1:要注意不等号的两边同时除以的是一个正数还是负数,若是负数则不等号的方向改变。比一比,谁做得又快又好!练
习小
结解一元一次不等式的一般步骤为:去分母
去括号
移项
合并同类项
系数化为1
小
结不等式移项法则:把不等式的任何一项改变符号后,从不等式的一边移到另一边,所得到的不等式仍然成立。 系数化为1:要注意不等号的两边同时除以的是一个正数还是负数,若是负数则不等号的方向改变。1、求不等式3(x-3)-1≤2x+2的正整数解。思考2、x取什么值时,代数式 的值。
(1)大于0 (2)不小于想
一
想
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
