华东师大版七级下册第7章《一次方程组》单元测试题(含答案)
文档属性
| 名称 | 华东师大版七级下册第7章《一次方程组》单元测试题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 193.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-09 17:14:00 | ||
图片预览


文档简介
华东师大版七级下册第7章《一次方程组》单元测试题
(满分100分)
姓名:___________班级:___________成绩:___________
一.选择题(共8小题,满分24分)
1.下列各方程:①4x﹣9=7﹣3x;②+=;③xy﹣y=1;④2x+3y=7.其中是二元一次方程的个数有几个( )
A.0 B.1 C.2 D.3
2.已知方程3x+2y=4,用含x的式子表示y,则( )
A. B.2y=3x﹣4 C.y= D.y=
3.下列方程中与方程x+y=1有公共解的是( )
A.y﹣4x=5 B.y=2x+5 C.2x﹣3y=﹣13 D.x=y﹣3
4.m为正整数,已知二元一次方程组有整数解,则m2﹣1的值为( )
A.3或48 B.3 C.4或49 D.48
5.老大爷背了一背鸡鸭到市场出售,单价是每只鸡100元,每只鸭80元,他出售完收入了660元,那么这背鸡鸭只数可能的方案有( )
A.4种 B.3种 C.2种 D.1种
6.利用加减消元法解方程组,下列做法正确的是( )
A.要消去y,可以将①×5+②×2
B.要消去x,可以将①×3+②×(﹣5)
C.要消去y,可以将①×5+②×3
D.要消去x,可以将①×(﹣5)+②×2
7.方程组的解的个数为( )
A.1 B.2 C.3 D.4
8.明代大数学家程大位著《算法统宗》一书中,记载了这样一道数学题:“八万三千短竹竿,将来要把笔头安,管三套五为期定,问都多少能完成?”用现代的话说就是:有83000根短竹,每根短竹可制成毛笔的笔管3个或笔套5个,怎样安排笔管和笔套的短竹的数量,使制成的1个笔管与1个笔套正好配套?设用于制作笔管的短竹数为x根,用于制作笔套的短竹数为y根,则可列方程为( )
A. B.
C. D.
二.填空题(共8小题,满分24分)
9.2元的人民币x张,5元的人民币y张,共120元,这个关系用方程可以表示为 .
10.若方程4xm﹣n﹣5ym+n=6是二元一次方程,则m= ,n= .
11.已知等式(2A﹣7B)x+(3A﹣8B)=8x+10对一切实数x都成立,则A= ,B= .
12.一个两位数,十位数字比个位数字大3,若将十位数字和个位数交换位置,所得的新两位数比原两位数的多15,则这个两位数是 .
13.若方程x﹣y=﹣1的一个解与方程组的解相同,则k的值为 .
14.已知是二元一次方程组的解,则m+3n的值为 .
15.定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3= .
16.已知x+2y﹣3z=0,2x+3y+5z=0,则= .
三.解答题(共7小题,满分52分)
17.解方程组:
①; ②.
18.二元一次方程组的解x,y的值相等,求k.
19.在解关于x、y的方程组 时,可以用①×2﹣②消去未知数x,也可以用①×4+②×3消去未知数y,试求a、b的值.
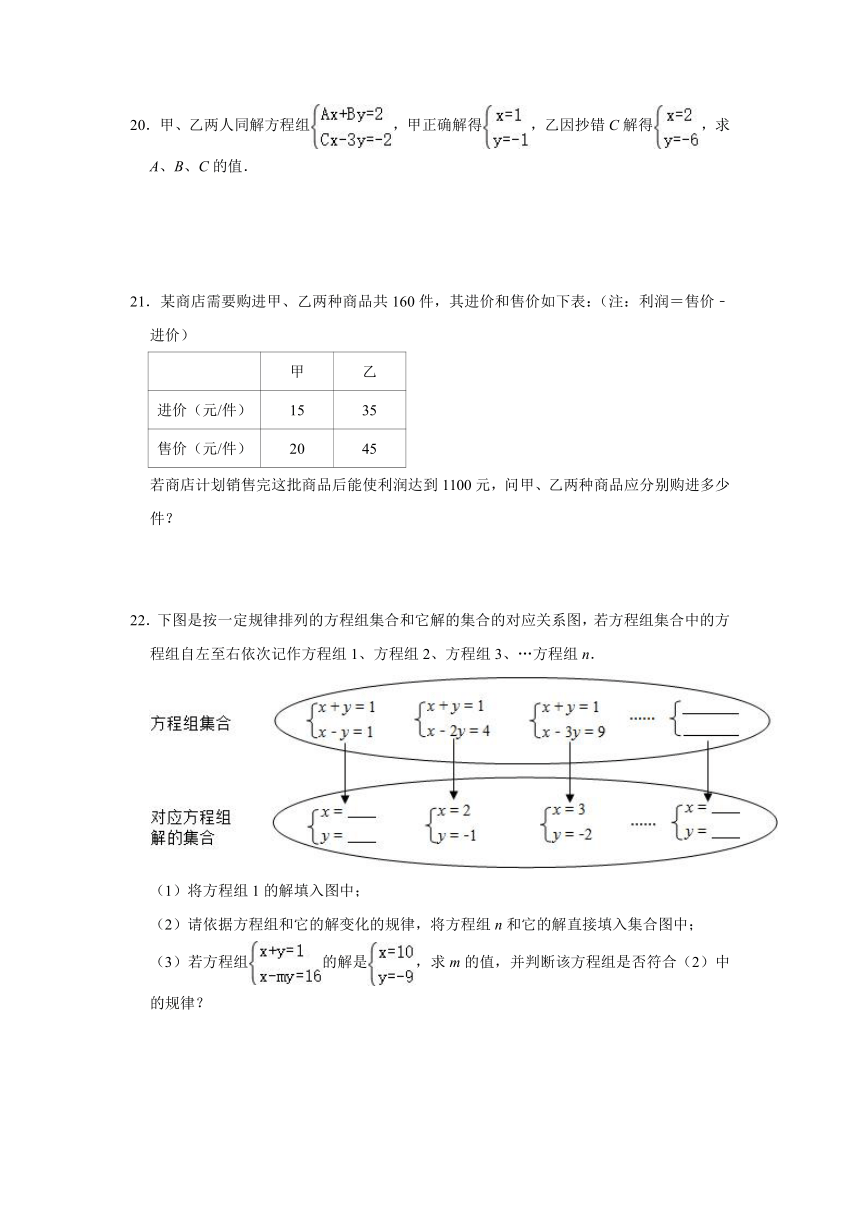
20.甲、乙两人同解方程组,甲正确解得,乙因抄错C解得,求A、B、C的值.
21.某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:利润=售价﹣进价)
甲 乙
进价(元/件) 15 35
售价(元/件) 20 45
若商店计划销售完这批商品后能使利润达到1100元,问甲、乙两种商品应分别购进多少件?
22.下图是按一定规律排列的方程组集合和它解的集合的对应关系图,若方程组集合中的方程组自左至右依次记作方程组1、方程组2、方程组3、…方程组n.
(1)将方程组1的解填入图中;
(2)请依据方程组和它的解变化的规律,将方程组n和它的解直接填入集合图中;
(3)若方程组的解是,求m的值,并判断该方程组是否符合(2)中的规律?
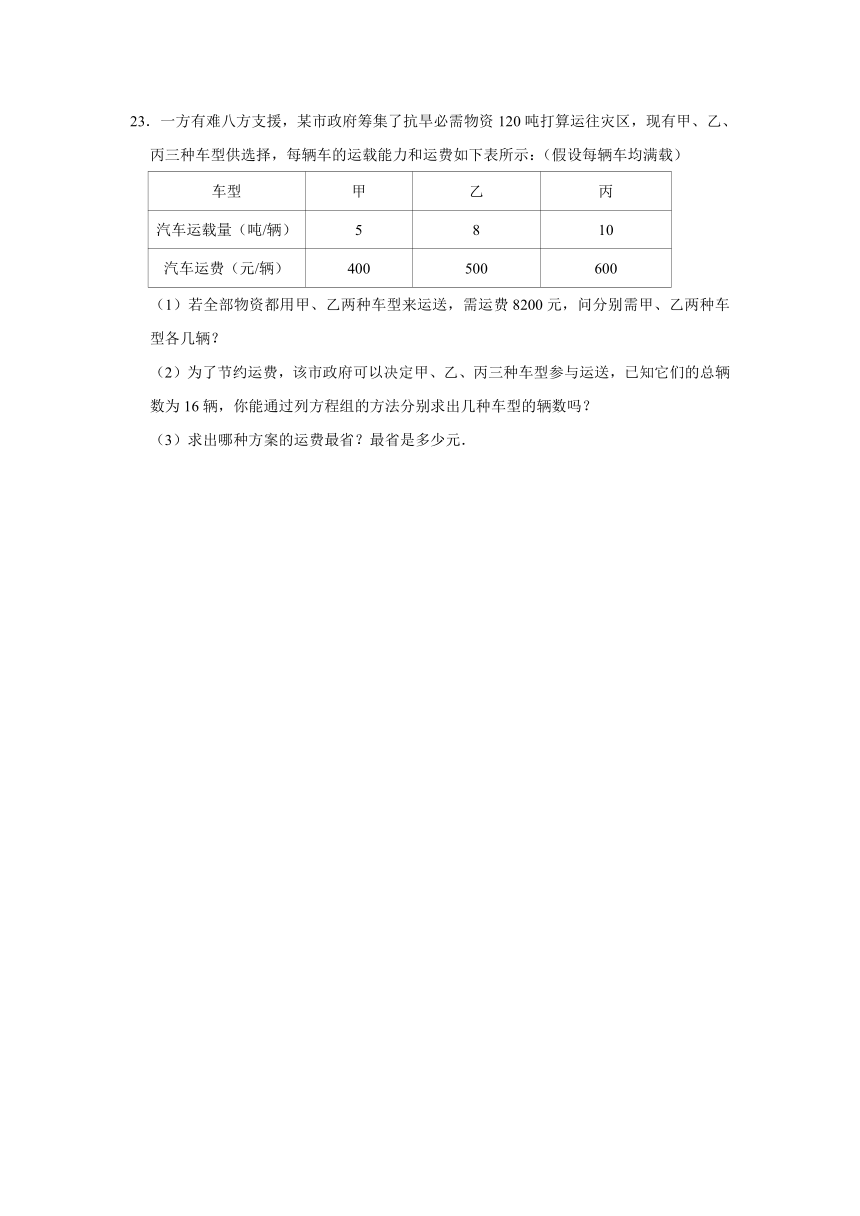
23.一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 甲 乙 丙
汽车运载量(吨/辆) 5 8 10
汽车运费(元/辆) 400 500 600
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以决定甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出哪种方案的运费最省?最省是多少元.
参考答案
一.选择题(共8小题)
1.【解答】解:①4x﹣9=7﹣3x,是一元一次方程;
②+=是分式方程;
③xy﹣y=1是二元二次方程;
④2x+3y=7是二元一次方程.
故选:B.
2.【解答】解:3x+2y=4,
解得:y=.
故选:A.
3.【解答】解:A、把x=﹣2,y=3代入y﹣4x=5,左边=3+8=11,右边=5,左边≠右边,故本选项错误;
B、把x=﹣2,y=3代入y=2x+5,左边=3,右边=1,左边≠右边,故本选项错误;
C、把x=﹣2,y=3代入2x﹣3y=﹣13,左边=﹣13,右边=﹣13,左边=右边,故本选项正确;
D、把x=﹣2,y=3代入x=y﹣3,左边=﹣2,右边=0,左边≠右边,故本选项错误;
故选:C.
4.【解答】解:,
①+②得:(m+3)x=10,
解得:x=,
把x=代入②得:y=,
由方程组为整数解,得到m+3=±1,m+3=±5,
解得:m=﹣2,﹣4,2,﹣8,
由m为正整数,得到m=2,
则原式=4﹣1=3,
故选:B.
5.【解答】解:设鸡有x只,鸭有y只,
依题意,得:100x+80y=660,
∴y=.
又∵x,y均为正整数,
∴或,
∴这背鸡鸭只数只有2种方案.
故选:C.
6.【解答】解:利用加减消元法解方程组,要消去x,可以将①×(﹣5)+②×2.
故选:D.
7.【解答】解:当x≥0,y≤0时,原方程组可化为:,解得;
由于y≤0,所以此种情况不成立.
当x≤0,y≥0时,原方程组可化为:,解得.
当x≥0,y≥0时,,无解;
当x≤0,y≤0时,,无解;
因此原方程组的解为:.
故选:A.
8.【解答】解:依题意,得:.
故选:B.
二.填空题(共8小题)
9.【解答】解:由题意得,2x+5y=120.
故答案为:2x+5y=120.
10.【解答】解:根据题意,得
解,得m=1,n=0.
故答案为:1,0.
11.【解答】解:由于等式(2A﹣7B)x+(3A﹣8B)=8x+10对一切实数x都成立,
所以,有
解得.
故答案为:,﹣.
12.【解答】解:设这个两位数的十位数字为x,个位数字为y,由题意得
解得:
∴这个两位数为63.
故答案为:63.
13.【解答】解:联立得:,
解得:,
代入方程得:2﹣6=k,
解得:k=﹣4,
故答案为:﹣4
14.【解答】解:把代入得,
①+②得m+3n=3,
故答案为:3.
15.【解答】解:根据题中的新定义化简已知等式得:,
解得:a=1,b=2,
则2*3=4a+3b=4+6=10,
故答案为:10.
16.【解答】解:由题意得:,
①×2﹣②得y=11z,
代入①得x=﹣19z,
原式===.
故本题答案为:.
三.解答题(共7小题)
17.【解答】解:(1)
①×2,得:6x﹣4y=12 ③,
②×3,得:6x+9y=51 ④,
则④﹣③得:13y=39,
解得:y=3,
将y=3代入①,得:3x﹣2×3=6,
解得:x=4.
故原方程组的解为:.
(2)
方程②两边同时乘以12得:3(x﹣3)﹣4(y﹣3)=1,
化简,得:3x﹣4y=﹣2 ③,
①+③,得:4x=12,
解得:x=3.
将x=3代入①,得:3+4y=14,
解得:y=.
故原方程组的解为:.
18.【解答】解:由题意可知x=y,
∴4x+3y=7可化为4x+3x=7,
∴x=1,y=1.
将x=1,y=1代入kx+(k﹣1)y=3中得:
k+k﹣1=3,
∴k=2
19.【解答】解:由题意可得:,
解之,,
所以a=6,b=.
20.【解答】解:把代入原方程组,得
,
把代入Ax+By=2,得
2A﹣6B=2.
可组成方程组,
解得.
21.【解答】解:设甲种商品应购进x件,乙种商品应购进y件,依题意得:
,
解得:,
答:甲种商品应购进100件,乙种商品应购进60件.
22.【解答】解:(1),
用(1)+(2),得2x=2,
∴x=1,
把x=1代入(1),得y=0,
∴;
(2),
;
(3)由题意,得10+9m=16,
解得m=,
该方程组为,它不符合(2)中的规律.
23.【解答】解:(1)设需甲车型x辆,乙车型y辆,得:解得
答:需甲车型8辆,需车型10辆;
(2)设需甲车型x辆,乙车型y辆,丙车型z辆,得:
消去z得5x+2y=40,x=,
因x,y是正整数,且不大于16,得y=5,10,15,
由z是正整数,解得,,
有两种运送方案:
①甲车型6辆,乙车型5辆,丙车型5辆;
②甲车型4辆,乙车型10辆,丙车型2辆;
(3)两种方案的运费分别是:
①400×6+500×5+600×5=7900;
②400×4+500×10+600×2=7800.
答:甲车型4辆,乙车型10辆,丙车型2辆,最少运费是7800元.
