12.1杠杆同步练习(含答案及解析)
图片预览

文档简介
人教版物理八年级下册 12.1 杠杆 同步练习
一、单选题(共11题)
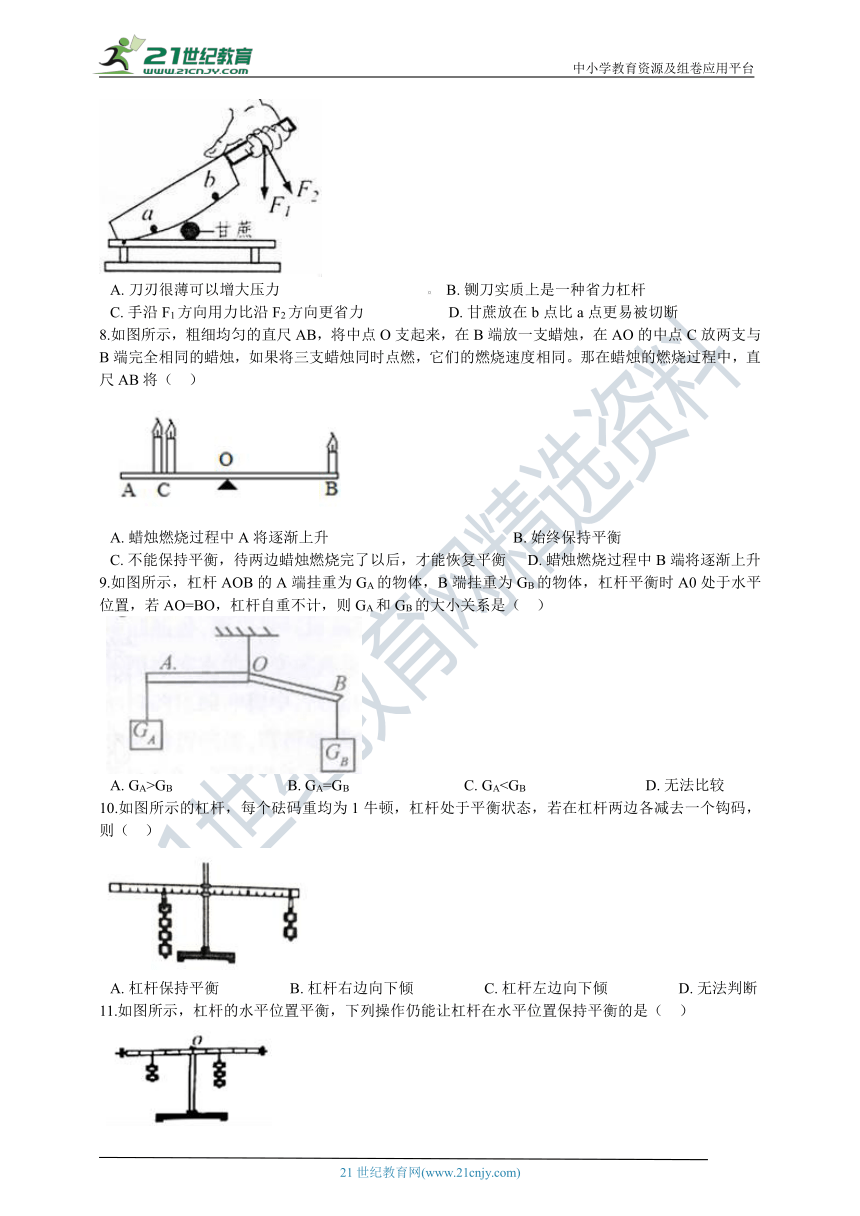
1.以下概念不是杠杆的基本要素的是( ??)
A.?支点????????????????????????????????????B.?动力????????????????????????????????????C.?阻力臂????????????????????????????????????D.?重心
2.下列简单机械中,属于费力杠杆的有(??? )
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?②④
3.如图是起重机用四种方案将地面上的一棵大树扶起的瞬间,其中拉力最小的是(?? )
A.?????????B.????????????C.????????????D.?
4.如图所示的杠杆AOB,O为支点,在B端挂一重物G,为了使杠杆在水平位置平衡,现在A端施加一个拉力,其中拉力最小的是(?? )
A.?F1?????????????????????????????????????????B.?F2 ?????????????????????????????????????????C.?F3?????????????????????????????????????????D.?F4
5.如图所示,轻质杠杆OA中点悬挂重为10N的物体,在A端施加一个始终垂直于杆向上的力F,匀速提升杠杆至水平位置B的过程中,力F将(? ),在B位置平衡时,拉力F的大小为( ??)
A.?不变?? 5N???????????????B.?变大 5N??????????????C.?变小 20N??????????????????D.?变大 20N
6.如图,用一个始终与杠杆垂直的力F,把杠杆OA从图示位置缓慢拉至水平的过程中,力F的大小将 (?? )
A.?变大??????????????????????B.?不变?????????????????????C.?变小??????????????????????????????????D.?不能确定
7.如图是一种切甘蔗用的铡刀示意图,下列说法中正确的是(? )
A.?刀刃很薄可以增大压力??????????????????????????????????????? B.?铡刀实质上是一种省力杠杆 C.?手沿F1方向用力比沿F2方向更省力??????????????????????D.?甘蔗放在b点比a点更易被切断
8.如图所示,粗细均匀的直尺AB,将中点O支起来,在B端放一支蜡烛,在AO的中点C放两支与B端完全相同的蜡烛,如果将三支蜡烛同时点燃,它们的燃烧速度相同。那在蜡烛的燃烧过程中,直尺AB将(?? )
?
A.?蜡烛燃烧过程中A将逐渐上升????????????????????????????????????????????????B.?始终保持平衡 C.?不能保持平衡,待两边蜡烛燃烧完了以后,才能恢复平衡?????D.?蜡烛燃烧过程中B端将逐渐上升
9.如图所示,杠杆AOB的A端挂重为GA的物体,B端挂重为GB的物体,杠杆平衡时A0处于水平位置,若AO=BO,杠杆自重不计,则GA和GB的大小关系是(?? )
A.?GA>GB??????????????????????????????B.?GA=GB??????????????????????????????C.?GA10.如图所示的杠杆,每个砝码重均为1牛顿,杠杆处于平衡状态,若在杠杆两边各减去一个钩码,则(?? )
A.?杠杆保持平衡??????????????????B.?杠杆右边向下倾??????????????????C.?杠杆左边向下倾??????????????????D.?无法判断
11.如图所示,杠杆的水平位置平衡,下列操作仍能让杠杆在水平位置保持平衡的是(?? )
A.?两侧钩码同时向外移一格??????????????????????????????????? ?B.?两侧钩码同时向内移一格 C.?左侧的钩码向内移一格,右侧减去一个钩码????????D.?在两侧钩码下方,同时加挂一个相同的钩码
二、填空题(共5题)
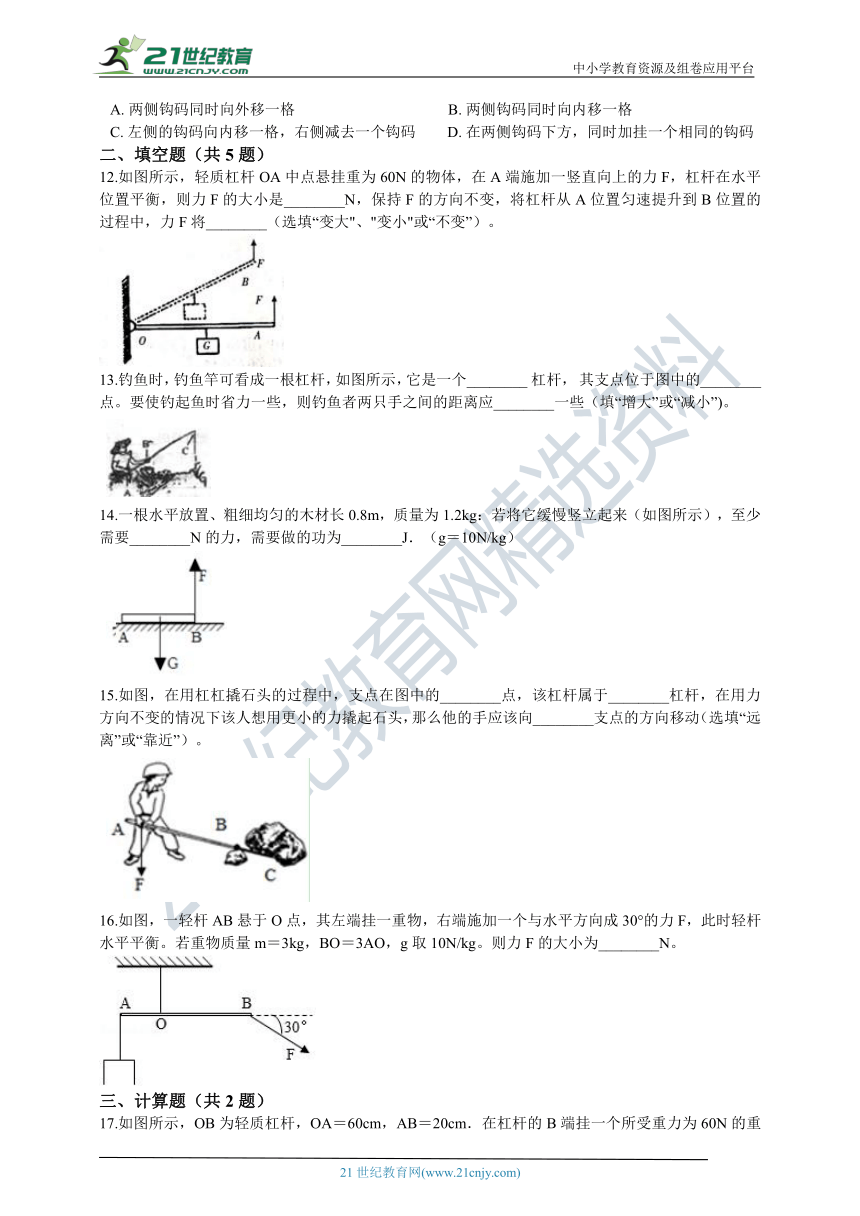
12.如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是________N,保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将________(选填“变大"、"变小"或“不变”)。
13.钓鱼时,钓鱼竿可看成一根杠杆,如图所示,它是一个________?杠杆, 其支点位于图中的________点。要使钓起鱼时省力一些,则钓鱼者两只手之间的距离应________一些(填“增大”或“减小”)。
14.一根水平放置、粗细均匀的木材长0.8m,质量为1.2kg:若将它缓慢竖立起来(如图所示),至少需要________N的力,需要做的功为________J.(g=10N/kg)
15.如图,在用杠杠撬石头的过程中,支点在图中的________点,该杠杆属于________杠杆,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向________支点的方向移动(选填“远离”或“靠近”)。
16.如图,一轻杆AB悬于O点,其左端挂一重物,右端施加一个与水平方向成30°的力F,此时轻杆水平平衡。若重物质量m=3kg,BO=3AO,g取10N/kg。则力F的大小为________N。
三、计算题(共2题)
17.如图所示,OB为轻质杠杆,OA=60cm,AB=20cm.在杠杆的B端挂一个所受重力为60N的重物,要使杠杆在水平位置上平衡,应在A点加一个多大的竖直向上的拉力?
18.如图所示,灯重30 N,灯挂在水平横杆的C端,O为杠杆的支点,水平杆OC长2 m,杆重不计,BC长0.5 m,绳子BD作用在横杆上的拉力是多少?(∠DBO= 30°)
四、实验探究题(共2题)
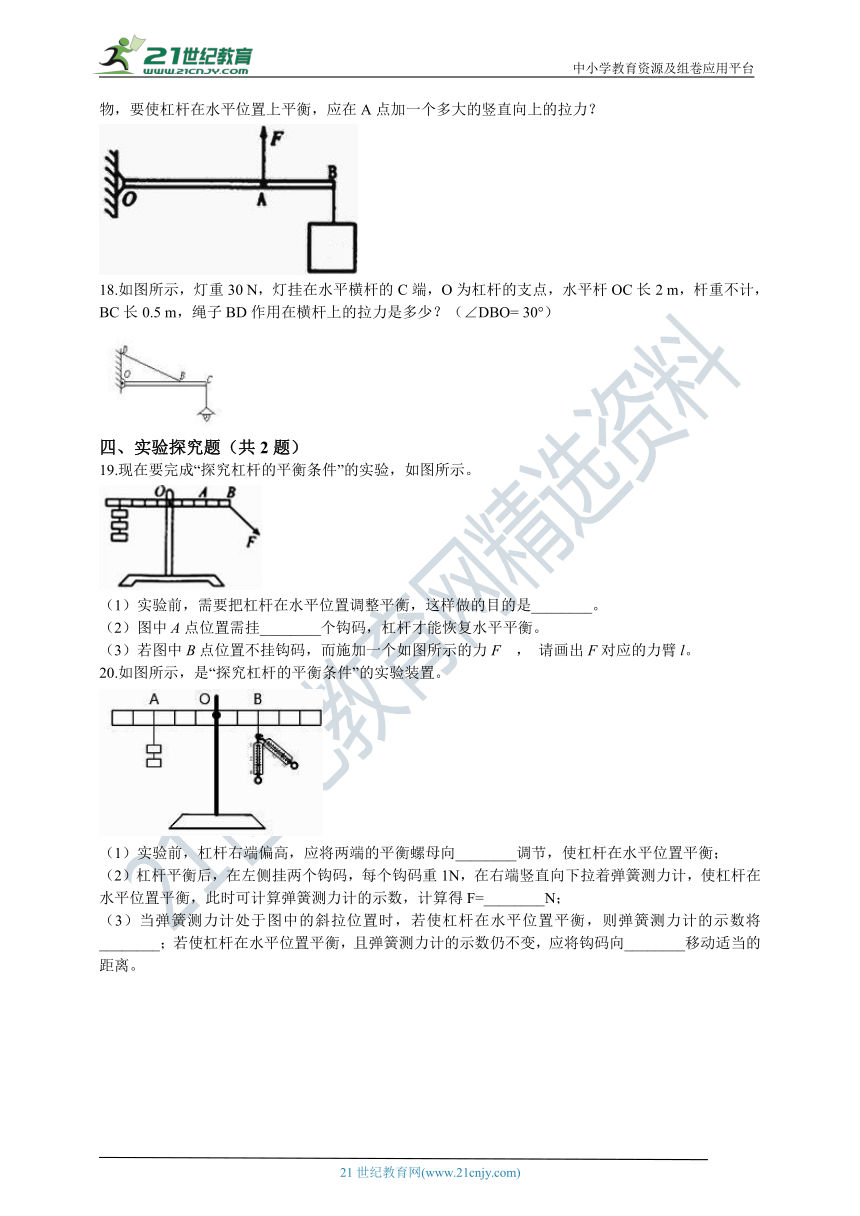
19.现在要完成“探究杠杆的平衡条件”的实验,如图所示。
(1)实验前,需要把杠杆在水平位置调整平衡,这样做的目的是________。
(2)图中A点位置需挂________个钩码,杠杆才能恢复水平平衡。
(3)若图中B点位置不挂钩码,而施加一个如图所示的力F , 请画出F对应的力臂l。
20.如图所示,是“探究杠杆的平衡条件”的实验装置。
(1)实验前,杠杆右端偏高,应将两端的平衡螺母向________调节,使杠杆在水平位置平衡;
(2)杠杆平衡后,在左侧挂两个钩码,每个钩码重1N,在右端竖直向下拉着弹簧测力计,使杠杆在水平位置平衡,此时可计算弹簧测力计的示数,计算得F=________N;
(3)当弹簧测力计处于图中的斜拉位置时,若使杠杆在水平位置平衡,则弹簧测力计的示数将________;若使杠杆在水平位置平衡,且弹簧测力计的示数仍不变,应将钩码向________移动适当的距离。
答案解析部分
一、单选题
1. D
解:杠杆的五要素是动力、动力臂、阻力、阻力臂、支点,故ABC符合题意,D不符合题意。 故答案为:D 【分析】杠杆的五要素是动力、动力臂、阻力、阻力臂、支点。
2. A
解:①钓鱼竿使用时,动力臂小于阻力臂,费力;②羊角锤使用时,动力臂大于阻力臂,省力;③使用筷子时,动力臂小于阻力臂,费力;④使用核桃夹时,动力臂大于阻力臂,省力,费力杠杆为①③,A符合题意。 故答案为:A。 【分析】根据使用杠杆时,动力臂和阻力臂的大小,分析杠杆是否能省力。
3. C
解:在杠杆上拉力最小时,力臂最大,杠杆上最大的力臂和相对应的力垂直,此时的力最小,C符合题意。 故答案为:C.
【分析】在杠杆上,最大的力臂是从支点到力的作用点的连线,最小的力和最大的力臂垂直。
4. B
解:由图可知,动力F4、F2都与OA垂直,则动力F4和F2对应的动力臂就是OA,它是最长的动力臂; 由F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小;因为F4和F2对应的动力臂最长,所以F4和F2最小; 为使杠杆平衡时,动力和阻力的转动效果是相反的,左边的阻力使杠杆有逆时针转动的效果,则右边的动力应有使杠杆顺时针转动的效果,即动力的方向应向下,所以可判断最小的力是F2。 故答案为:B。
【分析】由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小。所以要判断哪个动力最小,就看哪个动力对应的动力臂最长。支点与动力作用点之间的连线就是最长的动力臂,与这条动力臂垂直的力即为最小动力。
5. B
解:杠杆在B位置,LOB=2LOC , 由杠杆平衡得,FLOB=GLOC , 则
;
由题意知,力F始终垂直杠杆,动力臂不变,重物的重力不变,重物对杠杆的拉力不变,即阻力不变,当匀速提升杠杆至水平位置B的过程中阻力臂逐渐增大,结合杠杆的平衡条件FL1=GL2知,动力F1逐渐增大,B符合题意。
故答案为:B
【分析】 根据杠杆平衡条件分析解答; 杠杆平衡的条件:动力×动力臂=阻力×阻力臂.或写作:F 1L 1=F 2L 2? 。
6. A
解:把杠杆OA从图示位置缓慢拉至水平的过程中,动力臂OA的长度没有变化,阻力G的大小没有变化,而阻力臂l却逐渐增大;由杠杆的平衡条件可知:F×OA=G×l,当OA、G不变时,l越大,那么F越大,因此拉力F在这个过程中逐渐变大。
故答案为:A
【分析】利用杠杆的平衡条件分析解答.
7. B
解: A、刀刃很薄是通过减小接触面积来增大压强的,A不符合题意;
B、铡刀在使用时动力臂大于阻力臂,实质上是一种省力杠杆,B符合题意;
C、手沿F1方向用力比沿F2方向时的动力臂要小,根据杠杆平衡条件可知,动力越大,越费力,C不符合题意;
D、甘蔗放在a点比b点时的阻力臂更小,根据杠杆的平衡条件可知,动力会越小,更易被切断,D不符合题意。
故答案为:B
【分析】增大压强方法 :(1)S不变,F↑;(2)F不变,S↓? (3)? 同时把F↑,S↓.而减小压强方法则相反. 三种杠杆:(1)省力杠杆:L1>L2,平衡时F1F2.特点是费力,但省距离.(如钓鱼杠,理发剪刀等) (3)等臂杠杆:L1=L2,平衡时F1=F2.特点是既不省力,也不费力.(如:天平) ???? 在阻力不变的情况下,减小阻力臂,能减小动力;在阻力、阻力臂不变的情况下,动力臂越大,动力越小。
8. B
解:设一只蜡烛的质量为m,直尺长度为L,则2m× L=m× L,直尺在水平位置平衡;三支蜡烛同时点燃,并且燃烧速度相同,三支蜡烛因燃烧减少的质量m′相同,2(m﹣m′)× L=(m﹣m′)× L,因此在燃烧过程中直尺仍能平衡。
故答案为:B。
【分析】结合题意,理清动力臂、阻力臂的大小,利用杠杆的平衡条件分析解答.
9. C
解:力臂是支点到力的作用线的距离,画出两个的力臂,根据力臂的大小判断力的大小,如图: 根据杠杆平衡条件可知,, 由于, 所以 GA10. C
解:原来左边:4×5=20,右边:2×10=20,相等,所以杠杆平衡在杠杆两边各减去一个砝码后:左边3×5=15,右边:1×10=10,不相等,所以杠杆左边向下倾,C符合题意。
故答案为:C
【分析】利用杠杆的平衡条件分析解答即可.
11.C
解:设一个钩码的重力为G,横梁上一个格的长度为L,原来杠杆处于平衡状态,则有2G×3L=3G×2L;
A.两边各向外移一格,左边2G×4L=8GL<右边3G×3L=9GL,杠杆右端下沉;A不符合题意;
B.两边各往内移一格,左边2G×2L=4GL>右边3G×1L=3GL,杠杆左端下沉;B不符合题意;
C.左侧的钩码向内移一格,右侧减去一个钩码,左边2G×2L=4GL=右边2G×2L=4GL;杠杆平衡;C符合题意;
D.在两侧钩码下方,同时加挂一个相同的钩码,左边3G×2L=6GL,右边4G×2L=8GL,6GL<8GL,杠杆右端下沉,D不符合题意。
故答案为:C。
【分析】结合题意,利用杠杆的平衡条件分析即可.
二、填空题
12. 30;不变
解:动力臂是阻力臂的2倍,根据杠杆平衡条件计算拉力为, 由于杠杆上的拉力和阻力的力臂平行,在拉动过程中力臂的比值不变,所以拉力的大小不变。 故答案为:30;不变。 【分析】根据杠杆的平衡条件计算杠杆上力的大小,根据杠杆上力臂的关系判断力的大小变化。
13. 费力;A;增大
解:钓鱼竿的动力臂小于阻力臂,所以动力大于阻力,属于费力杠杆;使用钓鱼竿时,支点为A点,B点为动力点,C点为阻力点;要使钓起鱼时省力一些,应增大动力臂,所以钓鱼者两只手之间的距离应增大。 故答案为:费力;A;增大;
【分析】杠杆转动时,绕的点是杠杆的支点,杠杆分成费力杠杆、省力杠杆和等臂杠杆;省力杠杆:L1>L2 , F1F2 , 费力、省距离。如钓鱼竿、镊子、筷子、船桨、裁缝用的剪刀、理发师用的剪刀等。等臂杠杆:L1=L2 , F1=F2 , 既不省力也不费力,又不多移动距离,如天平、定滑轮等。
14. 6;4.8
解:(1)已知木材质量为1.2kg,则其重力G=mg=1.2kg×10N/kg=12N,设其长度为L;抬起一端时,以另一端为支点,其重心到支点的距离为 L,动力臂为L,根据杠杆平衡条件则有:F×L=G× L;解得F= G= ×12N=6N,即至少要用6N的力;(2)将它竖直起来时,木材的重心离水平面的高度为h= = =0.4m,则至少需要做的功:W=Gh=12N×0.4m=4.8J。 故答案为:6;4.8。
【分析】利用杠杆平衡条件:动力×动力臂=阻力×阻力臂可解答此题;再根据W=Gh求出需要做的功.
15. B;省力;远离
解:由图知,撬棒在使用过程中,绕B点转动,则B点为支点,并且动力臂大于阻力臂,是省力杠杆。由杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂越长越省力;所以,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向远离支点O方向移动,这样动力臂变长了,就越省力。 故答案为:B;省力;远离。
【分析】支点:杠杆绕着转动的点;再结合杠杆的平衡条件:动力×动力臂=阻力×阻力臂分析解答.
16. 20
解:反向延长力F的作用线,过支点O作力F作用线的垂线即为F的力臂L1 ,
因为右端施加一个与水平方向成30°的力F,则由几何知识可知L1= OB,
已知BO=3AO,重物质量m=3kg,则物体重力G=mg=3kg×10N/kg=30N,
由杠杆平衡条件得:G×L2=F×L1 ,
即G×OA=F× OB,
代入数据可得,30N×OA=F× ×3OA,
解得F=20N。
故答案为:20。
【分析】结合图像,利用杠杆的平衡条件分析求解,注意反向延长力F的作用线,过支点O作力F作用线的垂线即为F的力臂L1.
三、计算题
17.80N
解:由题图可知,OA为动力臂,等于60cm,OB为阻力臂,等于80cm,由杠杆平衡条件可知F·OA=G·OB,即F×60cm=60N×80cm,因此F=80N。 【分析】本题属于容易题,直接利用杠杆平衡条件F·OA=G·OB即可求解。
18.80N
解:绳子拉力的力臂如图所示: 由图可知,阻力力臂为OC=2m,OB=OC-BC=1.5m, 所以动力臂OE=OB×Sin∠DBO=0.75m 由杠杆平衡条件得: G×OC=F×OE;则 【分析】(1)杠杆的平衡条件:动力×动力臂=阻力×阻力臂;(2)本题为杠杆平衡题目,阻力力臂可以求出,只要求出动力力臂就可求出拉力。
四、实验探究题
19.(1)便于测量力臂 (2)4 (3)
解:(1)探究杠杆平衡的实验中,要使杠杆在水平位置平衡,这样力臂会在杠杆上,即这样做的目的是:便于测量力臂;(2)设杠杆每格的长度为L , 每个钩码重为G , 由图知道,此时左侧力与力臂的乘积是12GL , 若要使杠杆平衡,则右侧A点力与力臂的乘积也应是12GL , 所以,图中A点位置需挂4个钩码,杠杆才能恢复水平平衡;(3)由图知道,O为支点,延长力F的作用线,由支点O向F的作用线做垂线,标出F的力臂l , 如图:
【分析】探究杠杆平衡条件时,使杠杆在水平位置平衡,力臂在杠杆上,便于测量力臂,同时杠杆的重心通过支点,消除杠杆自重对杠杆平衡的影响;为得出普遍结论,用弹簧测力计拉杠杆,使力与杠杆不垂直,多做几次实验,得出实验结论.
20.(1)右 (2)3 (3)变大;右
解:(1)实验前,杠杆右端偏高,应将两端的平衡螺母向右调节,使杠杆在水平位置平衡;(2)由图可知:OB:OA=2:3,根据杠杆的平衡条件可得,F×OB=G×OA,F==2N×=3N;(3)斜向下拉时,阻力和阻力臂一定,动力臂变小,动力变大,所以,测力计的示数将变大;若使杠杆在水平位置平衡,且保持F大小不变,需要减小阻力臂,即应将钩码向右移动适当的距离。故答案为:(1)右;(2)3;(3)右。
【分析】(1)杠杆的调节也跟天平类似,应向高的一侧移动平衡螺母;(2)从图知道两边力臂的关系,利用杠杆的平衡条件求所需拉力大小;(3)当弹簧测力计斜着拉时,其力臂小于杠杆长,根据杠杆平衡条件分析出答案。
一、单选题(共11题)
1.以下概念不是杠杆的基本要素的是( ??)
A.?支点????????????????????????????????????B.?动力????????????????????????????????????C.?阻力臂????????????????????????????????????D.?重心
2.下列简单机械中,属于费力杠杆的有(??? )
A.?①③?????????????????????????????????????B.?②③?????????????????????????????????????C.?①④?????????????????????????????????????D.?②④
3.如图是起重机用四种方案将地面上的一棵大树扶起的瞬间,其中拉力最小的是(?? )
A.?????????B.????????????C.????????????D.?
4.如图所示的杠杆AOB,O为支点,在B端挂一重物G,为了使杠杆在水平位置平衡,现在A端施加一个拉力,其中拉力最小的是(?? )
A.?F1?????????????????????????????????????????B.?F2 ?????????????????????????????????????????C.?F3?????????????????????????????????????????D.?F4
5.如图所示,轻质杠杆OA中点悬挂重为10N的物体,在A端施加一个始终垂直于杆向上的力F,匀速提升杠杆至水平位置B的过程中,力F将(? ),在B位置平衡时,拉力F的大小为( ??)
A.?不变?? 5N???????????????B.?变大 5N??????????????C.?变小 20N??????????????????D.?变大 20N
6.如图,用一个始终与杠杆垂直的力F,把杠杆OA从图示位置缓慢拉至水平的过程中,力F的大小将 (?? )
A.?变大??????????????????????B.?不变?????????????????????C.?变小??????????????????????????????????D.?不能确定
7.如图是一种切甘蔗用的铡刀示意图,下列说法中正确的是(? )
A.?刀刃很薄可以增大压力??????????????????????????????????????? B.?铡刀实质上是一种省力杠杆 C.?手沿F1方向用力比沿F2方向更省力??????????????????????D.?甘蔗放在b点比a点更易被切断
8.如图所示,粗细均匀的直尺AB,将中点O支起来,在B端放一支蜡烛,在AO的中点C放两支与B端完全相同的蜡烛,如果将三支蜡烛同时点燃,它们的燃烧速度相同。那在蜡烛的燃烧过程中,直尺AB将(?? )
?
A.?蜡烛燃烧过程中A将逐渐上升????????????????????????????????????????????????B.?始终保持平衡 C.?不能保持平衡,待两边蜡烛燃烧完了以后,才能恢复平衡?????D.?蜡烛燃烧过程中B端将逐渐上升
9.如图所示,杠杆AOB的A端挂重为GA的物体,B端挂重为GB的物体,杠杆平衡时A0处于水平位置,若AO=BO,杠杆自重不计,则GA和GB的大小关系是(?? )
A.?GA>GB??????????????????????????????B.?GA=GB??????????????????????????????C.?GA
A.?杠杆保持平衡??????????????????B.?杠杆右边向下倾??????????????????C.?杠杆左边向下倾??????????????????D.?无法判断
11.如图所示,杠杆的水平位置平衡,下列操作仍能让杠杆在水平位置保持平衡的是(?? )
A.?两侧钩码同时向外移一格??????????????????????????????????? ?B.?两侧钩码同时向内移一格 C.?左侧的钩码向内移一格,右侧减去一个钩码????????D.?在两侧钩码下方,同时加挂一个相同的钩码
二、填空题(共5题)
12.如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是________N,保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将________(选填“变大"、"变小"或“不变”)。
13.钓鱼时,钓鱼竿可看成一根杠杆,如图所示,它是一个________?杠杆, 其支点位于图中的________点。要使钓起鱼时省力一些,则钓鱼者两只手之间的距离应________一些(填“增大”或“减小”)。
14.一根水平放置、粗细均匀的木材长0.8m,质量为1.2kg:若将它缓慢竖立起来(如图所示),至少需要________N的力,需要做的功为________J.(g=10N/kg)
15.如图,在用杠杠撬石头的过程中,支点在图中的________点,该杠杆属于________杠杆,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向________支点的方向移动(选填“远离”或“靠近”)。
16.如图,一轻杆AB悬于O点,其左端挂一重物,右端施加一个与水平方向成30°的力F,此时轻杆水平平衡。若重物质量m=3kg,BO=3AO,g取10N/kg。则力F的大小为________N。
三、计算题(共2题)
17.如图所示,OB为轻质杠杆,OA=60cm,AB=20cm.在杠杆的B端挂一个所受重力为60N的重物,要使杠杆在水平位置上平衡,应在A点加一个多大的竖直向上的拉力?
18.如图所示,灯重30 N,灯挂在水平横杆的C端,O为杠杆的支点,水平杆OC长2 m,杆重不计,BC长0.5 m,绳子BD作用在横杆上的拉力是多少?(∠DBO= 30°)
四、实验探究题(共2题)
19.现在要完成“探究杠杆的平衡条件”的实验,如图所示。
(1)实验前,需要把杠杆在水平位置调整平衡,这样做的目的是________。
(2)图中A点位置需挂________个钩码,杠杆才能恢复水平平衡。
(3)若图中B点位置不挂钩码,而施加一个如图所示的力F , 请画出F对应的力臂l。
20.如图所示,是“探究杠杆的平衡条件”的实验装置。
(1)实验前,杠杆右端偏高,应将两端的平衡螺母向________调节,使杠杆在水平位置平衡;
(2)杠杆平衡后,在左侧挂两个钩码,每个钩码重1N,在右端竖直向下拉着弹簧测力计,使杠杆在水平位置平衡,此时可计算弹簧测力计的示数,计算得F=________N;
(3)当弹簧测力计处于图中的斜拉位置时,若使杠杆在水平位置平衡,则弹簧测力计的示数将________;若使杠杆在水平位置平衡,且弹簧测力计的示数仍不变,应将钩码向________移动适当的距离。
答案解析部分
一、单选题
1. D
解:杠杆的五要素是动力、动力臂、阻力、阻力臂、支点,故ABC符合题意,D不符合题意。 故答案为:D 【分析】杠杆的五要素是动力、动力臂、阻力、阻力臂、支点。
2. A
解:①钓鱼竿使用时,动力臂小于阻力臂,费力;②羊角锤使用时,动力臂大于阻力臂,省力;③使用筷子时,动力臂小于阻力臂,费力;④使用核桃夹时,动力臂大于阻力臂,省力,费力杠杆为①③,A符合题意。 故答案为:A。 【分析】根据使用杠杆时,动力臂和阻力臂的大小,分析杠杆是否能省力。
3. C
解:在杠杆上拉力最小时,力臂最大,杠杆上最大的力臂和相对应的力垂直,此时的力最小,C符合题意。 故答案为:C.
【分析】在杠杆上,最大的力臂是从支点到力的作用点的连线,最小的力和最大的力臂垂直。
4. B
解:由图可知,动力F4、F2都与OA垂直,则动力F4和F2对应的动力臂就是OA,它是最长的动力臂; 由F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小;因为F4和F2对应的动力臂最长,所以F4和F2最小; 为使杠杆平衡时,动力和阻力的转动效果是相反的,左边的阻力使杠杆有逆时针转动的效果,则右边的动力应有使杠杆顺时针转动的效果,即动力的方向应向下,所以可判断最小的力是F2。 故答案为:B。
【分析】由杠杆平衡条件F1L1=F2L2可知,在阻力和阻力臂都一定的情况下,动力臂越长则动力越小。所以要判断哪个动力最小,就看哪个动力对应的动力臂最长。支点与动力作用点之间的连线就是最长的动力臂,与这条动力臂垂直的力即为最小动力。
5. B
解:杠杆在B位置,LOB=2LOC , 由杠杆平衡得,FLOB=GLOC , 则
;
由题意知,力F始终垂直杠杆,动力臂不变,重物的重力不变,重物对杠杆的拉力不变,即阻力不变,当匀速提升杠杆至水平位置B的过程中阻力臂逐渐增大,结合杠杆的平衡条件FL1=GL2知,动力F1逐渐增大,B符合题意。
故答案为:B
【分析】 根据杠杆平衡条件分析解答; 杠杆平衡的条件:动力×动力臂=阻力×阻力臂.或写作:F 1L 1=F 2L 2? 。
6. A
解:把杠杆OA从图示位置缓慢拉至水平的过程中,动力臂OA的长度没有变化,阻力G的大小没有变化,而阻力臂l却逐渐增大;由杠杆的平衡条件可知:F×OA=G×l,当OA、G不变时,l越大,那么F越大,因此拉力F在这个过程中逐渐变大。
故答案为:A
【分析】利用杠杆的平衡条件分析解答.
7. B
解: A、刀刃很薄是通过减小接触面积来增大压强的,A不符合题意;
B、铡刀在使用时动力臂大于阻力臂,实质上是一种省力杠杆,B符合题意;
C、手沿F1方向用力比沿F2方向时的动力臂要小,根据杠杆平衡条件可知,动力越大,越费力,C不符合题意;
D、甘蔗放在a点比b点时的阻力臂更小,根据杠杆的平衡条件可知,动力会越小,更易被切断,D不符合题意。
故答案为:B
【分析】增大压强方法 :(1)S不变,F↑;(2)F不变,S↓? (3)? 同时把F↑,S↓.而减小压强方法则相反. 三种杠杆:(1)省力杠杆:L1>L2,平衡时F1
8. B
解:设一只蜡烛的质量为m,直尺长度为L,则2m× L=m× L,直尺在水平位置平衡;三支蜡烛同时点燃,并且燃烧速度相同,三支蜡烛因燃烧减少的质量m′相同,2(m﹣m′)× L=(m﹣m′)× L,因此在燃烧过程中直尺仍能平衡。
故答案为:B。
【分析】结合题意,理清动力臂、阻力臂的大小,利用杠杆的平衡条件分析解答.
9. C
解:力臂是支点到力的作用线的距离,画出两个的力臂,根据力臂的大小判断力的大小,如图: 根据杠杆平衡条件可知,, 由于, 所以 GA
解:原来左边:4×5=20,右边:2×10=20,相等,所以杠杆平衡在杠杆两边各减去一个砝码后:左边3×5=15,右边:1×10=10,不相等,所以杠杆左边向下倾,C符合题意。
故答案为:C
【分析】利用杠杆的平衡条件分析解答即可.
11.C
解:设一个钩码的重力为G,横梁上一个格的长度为L,原来杠杆处于平衡状态,则有2G×3L=3G×2L;
A.两边各向外移一格,左边2G×4L=8GL<右边3G×3L=9GL,杠杆右端下沉;A不符合题意;
B.两边各往内移一格,左边2G×2L=4GL>右边3G×1L=3GL,杠杆左端下沉;B不符合题意;
C.左侧的钩码向内移一格,右侧减去一个钩码,左边2G×2L=4GL=右边2G×2L=4GL;杠杆平衡;C符合题意;
D.在两侧钩码下方,同时加挂一个相同的钩码,左边3G×2L=6GL,右边4G×2L=8GL,6GL<8GL,杠杆右端下沉,D不符合题意。
故答案为:C。
【分析】结合题意,利用杠杆的平衡条件分析即可.
二、填空题
12. 30;不变
解:动力臂是阻力臂的2倍,根据杠杆平衡条件计算拉力为, 由于杠杆上的拉力和阻力的力臂平行,在拉动过程中力臂的比值不变,所以拉力的大小不变。 故答案为:30;不变。 【分析】根据杠杆的平衡条件计算杠杆上力的大小,根据杠杆上力臂的关系判断力的大小变化。
13. 费力;A;增大
解:钓鱼竿的动力臂小于阻力臂,所以动力大于阻力,属于费力杠杆;使用钓鱼竿时,支点为A点,B点为动力点,C点为阻力点;要使钓起鱼时省力一些,应增大动力臂,所以钓鱼者两只手之间的距离应增大。 故答案为:费力;A;增大;
【分析】杠杆转动时,绕的点是杠杆的支点,杠杆分成费力杠杆、省力杠杆和等臂杠杆;省力杠杆:L1>L2 , F1
14. 6;4.8
解:(1)已知木材质量为1.2kg,则其重力G=mg=1.2kg×10N/kg=12N,设其长度为L;抬起一端时,以另一端为支点,其重心到支点的距离为 L,动力臂为L,根据杠杆平衡条件则有:F×L=G× L;解得F= G= ×12N=6N,即至少要用6N的力;(2)将它竖直起来时,木材的重心离水平面的高度为h= = =0.4m,则至少需要做的功:W=Gh=12N×0.4m=4.8J。 故答案为:6;4.8。
【分析】利用杠杆平衡条件:动力×动力臂=阻力×阻力臂可解答此题;再根据W=Gh求出需要做的功.
15. B;省力;远离
解:由图知,撬棒在使用过程中,绕B点转动,则B点为支点,并且动力臂大于阻力臂,是省力杠杆。由杠杆的平衡条件可知,在阻力和阻力臂不变的情况下,动力臂越长越省力;所以,在用力方向不变的情况下该人想用更小的力撬起石头,那么他的手应该向远离支点O方向移动,这样动力臂变长了,就越省力。 故答案为:B;省力;远离。
【分析】支点:杠杆绕着转动的点;再结合杠杆的平衡条件:动力×动力臂=阻力×阻力臂分析解答.
16. 20
解:反向延长力F的作用线,过支点O作力F作用线的垂线即为F的力臂L1 ,
因为右端施加一个与水平方向成30°的力F,则由几何知识可知L1= OB,
已知BO=3AO,重物质量m=3kg,则物体重力G=mg=3kg×10N/kg=30N,
由杠杆平衡条件得:G×L2=F×L1 ,
即G×OA=F× OB,
代入数据可得,30N×OA=F× ×3OA,
解得F=20N。
故答案为:20。
【分析】结合图像,利用杠杆的平衡条件分析求解,注意反向延长力F的作用线,过支点O作力F作用线的垂线即为F的力臂L1.
三、计算题
17.80N
解:由题图可知,OA为动力臂,等于60cm,OB为阻力臂,等于80cm,由杠杆平衡条件可知F·OA=G·OB,即F×60cm=60N×80cm,因此F=80N。 【分析】本题属于容易题,直接利用杠杆平衡条件F·OA=G·OB即可求解。
18.80N
解:绳子拉力的力臂如图所示: 由图可知,阻力力臂为OC=2m,OB=OC-BC=1.5m, 所以动力臂OE=OB×Sin∠DBO=0.75m 由杠杆平衡条件得: G×OC=F×OE;则 【分析】(1)杠杆的平衡条件:动力×动力臂=阻力×阻力臂;(2)本题为杠杆平衡题目,阻力力臂可以求出,只要求出动力力臂就可求出拉力。
四、实验探究题
19.(1)便于测量力臂 (2)4 (3)
解:(1)探究杠杆平衡的实验中,要使杠杆在水平位置平衡,这样力臂会在杠杆上,即这样做的目的是:便于测量力臂;(2)设杠杆每格的长度为L , 每个钩码重为G , 由图知道,此时左侧力与力臂的乘积是12GL , 若要使杠杆平衡,则右侧A点力与力臂的乘积也应是12GL , 所以,图中A点位置需挂4个钩码,杠杆才能恢复水平平衡;(3)由图知道,O为支点,延长力F的作用线,由支点O向F的作用线做垂线,标出F的力臂l , 如图:
【分析】探究杠杆平衡条件时,使杠杆在水平位置平衡,力臂在杠杆上,便于测量力臂,同时杠杆的重心通过支点,消除杠杆自重对杠杆平衡的影响;为得出普遍结论,用弹簧测力计拉杠杆,使力与杠杆不垂直,多做几次实验,得出实验结论.
20.(1)右 (2)3 (3)变大;右
解:(1)实验前,杠杆右端偏高,应将两端的平衡螺母向右调节,使杠杆在水平位置平衡;(2)由图可知:OB:OA=2:3,根据杠杆的平衡条件可得,F×OB=G×OA,F==2N×=3N;(3)斜向下拉时,阻力和阻力臂一定,动力臂变小,动力变大,所以,测力计的示数将变大;若使杠杆在水平位置平衡,且保持F大小不变,需要减小阻力臂,即应将钩码向右移动适当的距离。故答案为:(1)右;(2)3;(3)右。
【分析】(1)杠杆的调节也跟天平类似,应向高的一侧移动平衡螺母;(2)从图知道两边力臂的关系,利用杠杆的平衡条件求所需拉力大小;(3)当弹簧测力计斜着拉时,其力臂小于杠杆长,根据杠杆平衡条件分析出答案。
