12.3机械效率 同步练习(含答案及解析)
文档属性
| 名称 | 12.3机械效率 同步练习(含答案及解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-04-09 17:53:39 | ||
图片预览




文档简介
人教版物理八年级下册 12.3 机械效率 同步练习
一、单选题(共10题)
1.王强同学用水桶从水井中提水,在把水从井底提上来的过程中,下列说法正确的是( ???)
A.?对桶所做的功是有用功???????????????????????????????????????B.?对水所做的功是额外功 C.?对水所做的功是有用功???????????????????????????????????????D.?对水所做的功是总功
2.水桶掉进水里,打捞时桶里带些水,下列所述中属于有用功的是(?? )
A.?把桶中水提高做的功?????????B.?手对绳子拉力做的功?????????C.?把桶提高做的功????D.?提整个桶做的功
3.小明用滑轮组把一箱货物从一楼提升到五楼,给滑轮组加上润滑油后,机械效率提高了,则加润滑油后工人提升同样的重物仍从一楼升到五楼时,所做的功(?? )
A.?有用功减少,总功不变???????????????????????????????????????B.?有用功不变,总功增加 C.?有用功减少,总功减少???????????????????????????????????????D.?有用功不变,总功减少
4.将一个重为 4.5N 的物体沿斜面从底端匀速拉到顶端(如图所示),斜面长1.2m,高 0.4m,斜面对物体的摩擦力为 0.3N(物体大小可忽略)。则下列说法正确的是(??? )
A.?沿斜面向上的拉力为0.3N?????????????????????????????????? ?B.?拉力做的有用功0.36J,斜面的机械效率20% C.?拉力做的有用功1.8J,斜面的机械效率20%?????????D.?拉力做的总功2.16J,斜面机械效率83.3%
5.关于功率和机械效率,下列说法正确的是(?? )
A.?机械效率高的机械,功率一定大??????????????????????????????????? B.?做功时间长的机械,功率一定小 C.?由于存在机械重和摩擦,机械的机械效率小于100%?????D.?功率大的机械,做功一定多
6.一个滑轮组经改进后提高了机械效率,现用它把同一个物体提升相同的高度,则改进后与改进前相比(?? )
A.?有用功减少,总功减少了????????????????????????????????????B.?总功减少,额外功增加了 C.?有用功不变,额外功减少了????????????????????????????????D.?总功、有用功、额外功均减少了
7.如图所示,重8N的物体,在拉力F的作用下2s内匀速上升了0.4m,动滑轮重2N,不计绳重及摩擦,则下列计算结果错误的是(?? )
A.?拉力的大小为5N?????????????????????????????????????????????????B.?绳子自由端移动距离为1.2m C.?拉力F的功率为2W??????????????????????????????????????????????D.?滑轮组的机械效率为80%
8.如图,用同一滑轮组分别将物体A和物体B匀速提升相同的高度。与提升B相比,提升A的过程滑轮组的机械效率较大。若不计绳重与摩擦的影响,则提升A的过程(?? )
A.?额外功较小?????????????????????????B.?额外功较大?????????????????????????C.?总功较小?????????????????????????D.?总功较大
9.如图所示,将同一物体分别沿光滑的斜面AB、AC以相同的速度从底部匀速拉到顶点A,已知AB>AC,施加的力分别为F1、F2拉力做的功为W1、W2 , 拉力做功的功率分别为P1、P2 , 则下列判断中正确的是(?? )
A.?F1<F2 , W1=W2 , P1>P2????????????????????????????B.?F1>F2 , W1>W2 , P1>P2 C.?F1<F2 , W1<W2 , P1<P2???????????????????????????D.?F1<F2 , W1=W2 , P1<P2
10.图中剪刀剪纸机械效率为80%,这表示(? )
A.?若作用在剪刀的动力是1N,则阻力是0.8N B.?若作用在剪刀的阻力是1N,则动力是0.8N C.?若作用在剪刀的动力做功1J,则有0.2J 的功用于剪纸 D.?若作用在剪刀的动力做功1J,则有0.8J 的功用于剪纸
二、填空题(共6题)
11.如图,用2N的拉力匀速竖直向上拉绳子自由端,将重为3.5N物体提升0.1m,不计绳重与摩擦,动滑轮机械效率为________?;若物体重变大,则滑轮机械效率将________。
12.如图所示,小明用一个重为10N的动滑轮匀速提起40N的重物,在忽略绳重及摩擦的情况下,拉力F=________N,动滑轮的机械效率是________。
13.如图所示,工人用250N的力F将重为600N的物体在10s内匀速提升2m,则此过程中,拉力做的功为________J,滑轮组的机械效率为________。
14.请在图中用笔画线代替绳子,将两个滑轮连成滑轮组,要求人往下拉绳使重物升起________。现在用这个装置将重为400N的货物竖直匀速提高了2m,他所做的有用功是________J,已知该滑轮组的机械效率为80%,工人的拉力是________N.要提高该滑轮组的机械效率,你的方法是________。
15.使用滑轮组把200N重物提高0.6m时,绳子被拉下3m , 用的拉力是50N , 则滑轮组的机械效率为________。
16.如图所示,把重力为600N的物体匀速推到斜面顶端,斜面长为2m,高为1m,实际推力为400N,所花时间为5s。那么,将物体从底部推到顶部所做的有用功是________J,推力做功________J,推力的功率是________W,物体与斜面间的摩擦力是________N,整个装置的机械效率是________。
三、实验探究题(共2题)
17.如图所示为测量滑轮组机械效率的实验装置,钩码总重6N。
(1)实验室要竖直向上________拉动弹簧测力计,由图中可知拉力大小为________N,将弹簧测力计向上移动15cm,则钩码上升高度为________cm,有用功为________J;总功为________J;该轮滑组的机械效率为________。
(2)取下2个钩码,再做实验,此时滑轮组的机械效率将________(选填:“增大”、“减小”或“不变”)
18.小周同学在学过有关“机械效率”的知识后提出了一个问题:“斜面的机械效率与斜面的倾斜程度有没有关系?”针对这个问题他做了在斜面上匀速拉动小车的探究实验,并记录实验数据如下:
斜需倾斜程度
小车重G/N
小车上升高试h/m
沿斜面拉力F/N
小车行色匆匆 动距离s/m
有用功W有/J
总功W W总/J
机械效率
较缓
10
0.1
3
1
1
3
33%
较陡
10
0.2
4
1
最陡
10
0.4
6
1
4
6
67%
请根据以上实验数据回答:
(1)“较陡”时,做的有用功为________,总功为________,机械效率为________
(2)通过对上述实验数据的分析,你对小周提出的问题可获得的初步结论是:________
(3)如果小周还想探究斜面的机械效率与物重的关系,实验时应该控制哪些条件不变?
四、计算题(共2题)
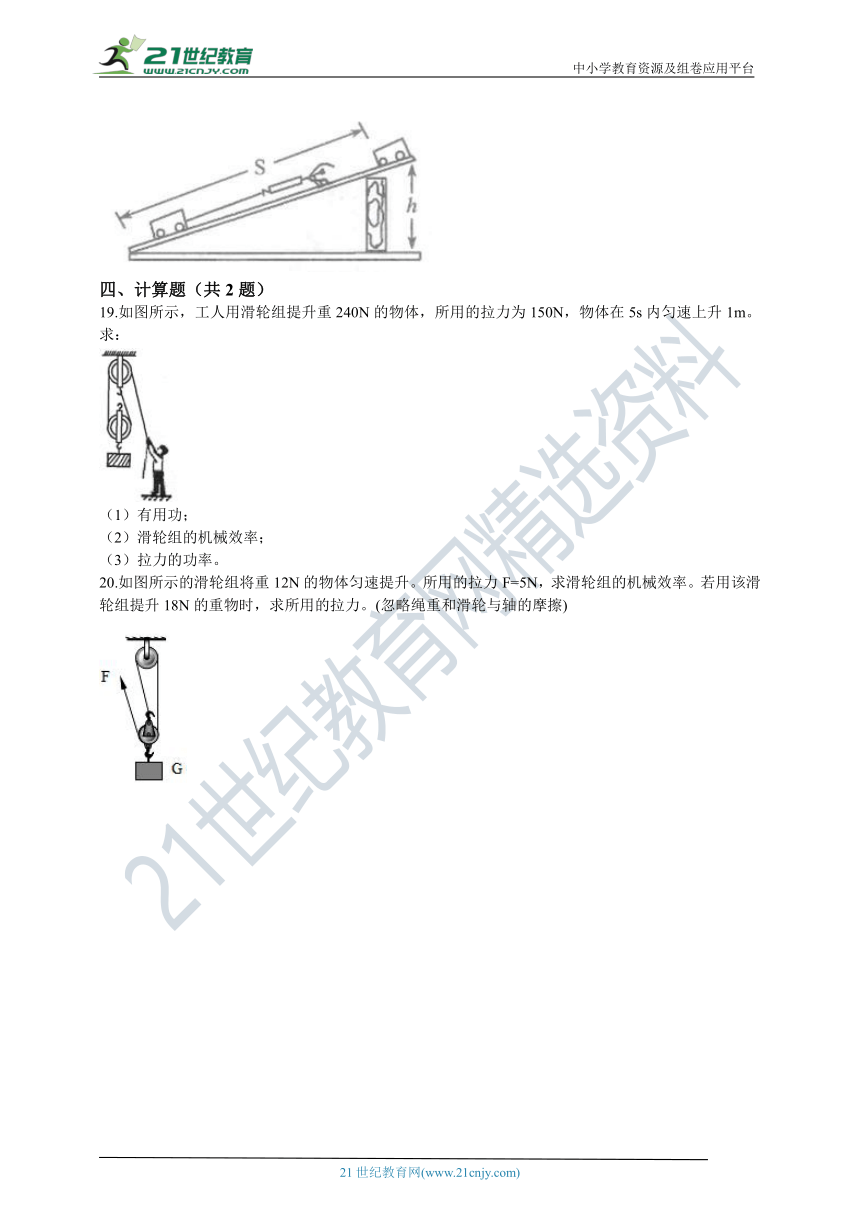
19.如图所示,工人用滑轮组提升重240N的物体,所用的拉力为150N,物体在5s内匀速上升1m。求:
(1)有用功;
(2)滑轮组的机械效率;
(3)拉力的功率。
20.如图所示的滑轮组将重12N的物体匀速提升。所用的拉力F=5N,求滑轮组的机械效率。若用该滑轮组提升18N的重物时,求所用的拉力。(忽略绳重和滑轮与轴的摩擦)
答案解析部分
一、单选题
1. C
解:利用水桶把水从水井提上来,对水做的功的有用功,对桶做的功是额外功,人做的功是总功,C符合题意。 故答案为:C. 【分析】人想要做的功的是有用功,人不想做又不得不做的功是额外功。
2. C
解:A、把桶中水提高做的功属于额外功;A不符合题意; B、手对绳子拉力做的功属于额外功;B不符合题意; C、把桶提高做的功属于有用功;C符合题意; D、提整个桶做的功属于总功;D不符合题意; 故答案为:C。
【分析】本题的目的是打捞水桶,所以对木桶做的功属于有用功。做功的两个必要因素:作用在物体上的力和物体在力的方向上通过的距离;有用功的定义:当一个力作用在物体上,并使物体在力的方向上通过了一段距离,力学中就说这个力对物体做了功;额外功是并非我们需要但又不得不额外做的功;额外功加有用功就是总功。
3. D
解:加润滑油后工人提升同样的重物时,物体的重力不变、提升高度不变(都提升到五楼),根据W有=Gh可知,有用功不变;但加了润滑油后,额外功变小,因总功等于有用功加上额外功,所以工人做的总功变小。
故答案为:D
【分析】根据W有=Gh可知有用功变化情况;但加了润滑油后,额外功变小,因总功等于有用功加上额外功,可知工人做的总功变化情况.
4. D
解:物体上升做的有用功为, 克服摩擦的额外功为, 总功为W=1.8J+0.36J=2.16J,拉力为, 机械效率为, D符合题意,ABC不符合题意。 故答案为:D.
【分析】根据物体的重力和高度的乘积计算有用功,利用摩擦力和长度计算额外功,利用总功和斜面长度计算拉力,有用功和总功的比值计算机械效率。
5. C
解:机械效率表示有用功和总功的比值大小,由于额外功的存在,机械效率小于100%,功率表做功的快慢,不是做功的多少,C符合题意。 故答案为:C. 【分析】机械效率是有用功和总功的比值,由于额外功的存在,机械效率小于100%,功率表做功的快慢。
6. C
解: AD、把同一物体匀速提升同样的高度,由W有用=Gh可知,前后两次做的有用功不变,此AD不符合题意;
BC、有用功一定,机械效率增加,由公式η= = 知:总功减小,额外功减小。C符合题意、B不符合题意。
故答案为:C。
【分析】结合W有用=Gh可知前后两次做的有用功不变,再结合公式η= = ?分析理解.
7. B
解: A、如图滑轮组,承担物重的绳子股数n=2,
不计绳重和摩擦,拉力F的大小:
F= (G物+G动)= ×(8N+2N)=5N,A符合题意;
B、绳子自由端移动距离:
s=2h=2×0.4m=0.8m,B不符合题意;
C、拉力F做的总功:
W总=Fs=5N×0.8m=4J,
拉力做功的功率:
P= = =2W,C符合题意;
D、使用滑轮组做的有用功:
W有用=Gh=8N×0.4m=3.2J,
滑轮组的机械效率:
η= = ×100%=80%,D符合题意。
故答案为:B。
【分析】利用W有用=Gh求出有用功.利用W总=Fs=Fnh求拉力做功;再利用功率公式P=求拉力做功的功率;利用 η=?计算滑轮组的机械效率.
8. D
解: AB、由题知,提起两物体所用的滑轮组相同,将物体提升相同的高度,不计绳重和摩擦,克服动滑轮重力所做的功是额外功,由W额=G动h知,提升A和B所做额外功相同,A、B不符合题意;
CD、不计绳重与摩擦的影响,滑轮组的机械效率:η= = ,额外功相同,提升A物体时滑轮组的机械效率较大,所以提升A物体所做的有用功较大,其总功较大,C不符合题意、D符合题意。
故答案为:D。
【分析】不计绳重及摩擦,利用相同的滑轮和绳子、提升相同的高度,做额外功相同;而总功等于有用功与额外功之和; 机械效率是有用功与总功的比值,据此分析解答即可.
9. D
解:将同一物体分别沿光滑斜面(无摩擦力)AB、AC以相同的速度,匀速拉到顶点A,拉力F1、F2对物体所做的功等于物体克服重力所做的功,而同一物体升高相同的高度克服重力做的功相同,故W1=W2;又因 ,W相同,AB>AC,所以F1<F2 , 再由 知,速度相同,F1<F2 , 则P1<P2.
故答案为:D.
【分析】斜面越长,越省力,利用物体的重力和上升的高度可以计算有用功,功和时间的比值计算功率。
10. D
解:A. B. 剪刀使用时,其转轴处会存在摩擦力,且剪刀为一杠杆,使用时,阻力臂是变化的,故不能确定阻力或动力的大小,AB不符合题意;
C. D. 机械效率为有用功与总功的比,机械效率为80%时,若作用在剪刀的动力做功1J,表示有0.8J 的功用于剪纸;另外0.2J 的功是克服摩擦做的额外功,C不符合题意,D符合题意;
故答案为:D。
【分析】机械效率是有用功和总功的比值.
二、填空题
11. 87.5%;增大 解:(1)动滑轮上承担重力的绳子有2段,那么动滑轮的机械效率为:; (2)根据机械效率可知:当物重G增大时,而动滑轮的重力G动不变时,滑轮组的机械效率增大。 【分析】(1)使用动滑轮提升重物时,对物体做有用功,对动滑轮做额外功,可根据计算机械效率; (2)动滑轮的机械效率还可根据计算;物重增大,即G增大,分析分数值的变化即可。
12. 25;80%
解:忽略绳重及摩擦,拉力F= (G+G动)= ×(40N+10N)=25N;动滑轮的机械效率:η= =80%。 故答案为:25;80%. 【分析】忽略绳重及摩擦,拉力F= (G+G动);再利用η= 求得动滑轮的机械效率.
13. 1500;80%
解:由图知n=3,则绳子自由端移动的距离:s=3h=3×2m=6m,
拉力做的总功:
W总=Fs=250N×6m=1500J;
工人做的有用功:
W有=Gh=600N×2m=1200J,
滑轮组的机械效率:
η= = ×100%=80%。
故答案为:1500;80%;
【分析】利用W总=Fs=Fnh求得拉力做的总功,再利用W有=Gh求得工人做的有用功,最后用η= 求得滑轮组的机械效率.
14. ;800;250;增加提升的物重
解:(1)人向下拉绳使重物升起,说明绳子最后绕过的是定滑轮,按此反向绕线,则绳子的起始端应系在定滑轮的挂钩上,如图所示:
;(2)他所做的有用功:
W有用=Gh=400N×2m=800J;(3)由图知n=2,拉力端移动距离s=2h,
滑轮组η= = = = ,
则工人的拉力:
F= = =250N;(4)要提高机械效率,要尽量减小额外功、增大有用功,可增大使用滑轮组提升的物重、在转轴上加润滑油、减轻动滑轮的自重等。
故答案为:如图所示;800; 250;增加提升的物重。
【分析】以人手为起点开始绕线,利用W有用=Gh求得有用功,利用η= = 求得工人的拉力.要提高机械效率,要尽量减小额外功、增大有用功,据此分析即可.
15. 80%
解:拉力做的有用功:
W有用=Gh=200N×0.6m=120J,
拉力做的总功:
W总=Fs=50N×3m=150J,
滑轮组的机械效率:
η= = ×100%=80%。
故答案为:80%。
【分析】利用W有用=Gh求得有用功,再利用W总=Fs求得拉力做的总功,最后利用η= 求得滑轮组的机械效率.
16. 600;800;160;100;75%???
解:由题知,斜面长s=2m,斜面高h=1m,物体重G=600N,推力F=400N;
有用功:W有用=Gh=600N×1m=600J,推力做的总功:W总=Fs=400N×2m=800J,
推力做的总功的功率:P= ?=160W;额外功:W额外=W总?W有用=800J?600J=200J,
由W额外=fs得摩擦力: f= =100N;斜面的机械效率:η= ?=75%
故答案为:600;800;160;100;75%. 【分析】提升重物做的功是有用功,克服摩擦力所做的功是额外功,推力做的功是总功,推力做的总功的功率是总功率,利用η= 计算斜面的机械效率.
?
三、实验探究题
17. (1)匀速;2.4;5;0.3;0.36;83.3% (2)减小
解:(1)①实验中要竖直向上匀速拉动弹簧测力计,弹簧测力计示数稳定,便于读数;
②图中弹簧测力计每一个大格代表1N,每一个小格代表0.2N,拉力大小为2.4N;
③由图可知承担物重的绳子股数n=3,则钩码上升的高度h= = =5cm;
④W有用=Gh=6N×0.05m=0.3J,
W总=Fs=2.4N×0.15m=0.36J;滑轮组的机械效率:η= = ×100%=83.3%。(2)取下2个钩码后,则所做的有用功减小,而额外功不变,所以有用功在总功所占的比例减小,则滑轮组的机械效率将减小。故答案为:(1)匀速;2.4;5;0.3;0.36;83.3%;(2)减小
【分析】(1)拉力做的功为总功,克服重力做的功为有用功,有用功除以总功即为机械效率; (2)结合第一问求解的机械效率的表达式分析求解即可。
18. (1)2J;4J;50% (2)在其他条件不变的情况下,斜面越陡,机械效率越高 (3)斜面的倾斜程度、斜面与物体接触面的粗糙程度
解:(1)“较陡”时,做的有用功W有用 =GH=10N×0.2m=2J , 总功W总=FS=4N×1m=4J , 机械效率; (2)分析表中的机械效率的值可以看出:在其他条件不变的情况下,斜面越陡,机械效率越高; (3)要探究斜面机械效率与物重的关系 , 需要使斜面的倾斜程度相同 , 同时控制小车上升的高度(或小车在斜面上移动的距离),而改变物体的重力。 故答案为:(1)2J ; 4J ; 50% ; (2)在其他条件不变的情况下,斜面越陡,机械效率越高;(3)斜面的倾斜程度、斜面与物体接触面的粗糙程度。 【分析】(1)结合表中的数据,利用公式W=Gh计算出有用功,利用公式W=Fs计算总功,再根据公式计算机械效率; (2)分析表格中数据 , 斜面的倾斜程度逐渐变大 , 比较机械效率的值,得出结论; (3)要探究斜面机械效率与物重的关系 , 需要使斜面的倾斜程度相同 , 同时控制小车上升的高度(或小车在斜面上移动的距离),而改变物体的重力 , 分别测量不同重力时斜面的机械效率 , 分析得出结论。
四、计算题
19. (1)解:W有=Gh=240N×1m=240J;
答:有用功为240J
(2)解:W总=FS=150N×2m=300J;
∴η= = =80%;
答:滑轮组的机械效率为80%
(3)解:P= = =60W;
答:拉力的功率为60W
【分析】(1)(2)拉力做的功为总功,克服重力做的功为有用功,有用功除以总功即为机械效率; (3)利用拉力作的功除以做功的时间即为功率。
20. 解:η=W有用/W总=Gh/Fs=G/nP=12N/(3×5N)=80%
G动=nF-G=3×5N-12N=3N
F=(G物+G动)/n=(18N+3N)/3=7N
【分析】根据拉力和物体的重力,结合滑轮组的绳子股数,可以计算机械效率的大小,根据拉力和物体的重力还可以计算动滑轮的重力,结合物体重力和动滑轮的重力计算总的拉力大小。
一、单选题(共10题)
1.王强同学用水桶从水井中提水,在把水从井底提上来的过程中,下列说法正确的是( ???)
A.?对桶所做的功是有用功???????????????????????????????????????B.?对水所做的功是额外功 C.?对水所做的功是有用功???????????????????????????????????????D.?对水所做的功是总功
2.水桶掉进水里,打捞时桶里带些水,下列所述中属于有用功的是(?? )
A.?把桶中水提高做的功?????????B.?手对绳子拉力做的功?????????C.?把桶提高做的功????D.?提整个桶做的功
3.小明用滑轮组把一箱货物从一楼提升到五楼,给滑轮组加上润滑油后,机械效率提高了,则加润滑油后工人提升同样的重物仍从一楼升到五楼时,所做的功(?? )
A.?有用功减少,总功不变???????????????????????????????????????B.?有用功不变,总功增加 C.?有用功减少,总功减少???????????????????????????????????????D.?有用功不变,总功减少
4.将一个重为 4.5N 的物体沿斜面从底端匀速拉到顶端(如图所示),斜面长1.2m,高 0.4m,斜面对物体的摩擦力为 0.3N(物体大小可忽略)。则下列说法正确的是(??? )
A.?沿斜面向上的拉力为0.3N?????????????????????????????????? ?B.?拉力做的有用功0.36J,斜面的机械效率20% C.?拉力做的有用功1.8J,斜面的机械效率20%?????????D.?拉力做的总功2.16J,斜面机械效率83.3%
5.关于功率和机械效率,下列说法正确的是(?? )
A.?机械效率高的机械,功率一定大??????????????????????????????????? B.?做功时间长的机械,功率一定小 C.?由于存在机械重和摩擦,机械的机械效率小于100%?????D.?功率大的机械,做功一定多
6.一个滑轮组经改进后提高了机械效率,现用它把同一个物体提升相同的高度,则改进后与改进前相比(?? )
A.?有用功减少,总功减少了????????????????????????????????????B.?总功减少,额外功增加了 C.?有用功不变,额外功减少了????????????????????????????????D.?总功、有用功、额外功均减少了
7.如图所示,重8N的物体,在拉力F的作用下2s内匀速上升了0.4m,动滑轮重2N,不计绳重及摩擦,则下列计算结果错误的是(?? )
A.?拉力的大小为5N?????????????????????????????????????????????????B.?绳子自由端移动距离为1.2m C.?拉力F的功率为2W??????????????????????????????????????????????D.?滑轮组的机械效率为80%
8.如图,用同一滑轮组分别将物体A和物体B匀速提升相同的高度。与提升B相比,提升A的过程滑轮组的机械效率较大。若不计绳重与摩擦的影响,则提升A的过程(?? )
A.?额外功较小?????????????????????????B.?额外功较大?????????????????????????C.?总功较小?????????????????????????D.?总功较大
9.如图所示,将同一物体分别沿光滑的斜面AB、AC以相同的速度从底部匀速拉到顶点A,已知AB>AC,施加的力分别为F1、F2拉力做的功为W1、W2 , 拉力做功的功率分别为P1、P2 , 则下列判断中正确的是(?? )
A.?F1<F2 , W1=W2 , P1>P2????????????????????????????B.?F1>F2 , W1>W2 , P1>P2 C.?F1<F2 , W1<W2 , P1<P2???????????????????????????D.?F1<F2 , W1=W2 , P1<P2
10.图中剪刀剪纸机械效率为80%,这表示(? )
A.?若作用在剪刀的动力是1N,则阻力是0.8N B.?若作用在剪刀的阻力是1N,则动力是0.8N C.?若作用在剪刀的动力做功1J,则有0.2J 的功用于剪纸 D.?若作用在剪刀的动力做功1J,则有0.8J 的功用于剪纸
二、填空题(共6题)
11.如图,用2N的拉力匀速竖直向上拉绳子自由端,将重为3.5N物体提升0.1m,不计绳重与摩擦,动滑轮机械效率为________?;若物体重变大,则滑轮机械效率将________。
12.如图所示,小明用一个重为10N的动滑轮匀速提起40N的重物,在忽略绳重及摩擦的情况下,拉力F=________N,动滑轮的机械效率是________。
13.如图所示,工人用250N的力F将重为600N的物体在10s内匀速提升2m,则此过程中,拉力做的功为________J,滑轮组的机械效率为________。
14.请在图中用笔画线代替绳子,将两个滑轮连成滑轮组,要求人往下拉绳使重物升起________。现在用这个装置将重为400N的货物竖直匀速提高了2m,他所做的有用功是________J,已知该滑轮组的机械效率为80%,工人的拉力是________N.要提高该滑轮组的机械效率,你的方法是________。
15.使用滑轮组把200N重物提高0.6m时,绳子被拉下3m , 用的拉力是50N , 则滑轮组的机械效率为________。
16.如图所示,把重力为600N的物体匀速推到斜面顶端,斜面长为2m,高为1m,实际推力为400N,所花时间为5s。那么,将物体从底部推到顶部所做的有用功是________J,推力做功________J,推力的功率是________W,物体与斜面间的摩擦力是________N,整个装置的机械效率是________。
三、实验探究题(共2题)
17.如图所示为测量滑轮组机械效率的实验装置,钩码总重6N。
(1)实验室要竖直向上________拉动弹簧测力计,由图中可知拉力大小为________N,将弹簧测力计向上移动15cm,则钩码上升高度为________cm,有用功为________J;总功为________J;该轮滑组的机械效率为________。
(2)取下2个钩码,再做实验,此时滑轮组的机械效率将________(选填:“增大”、“减小”或“不变”)
18.小周同学在学过有关“机械效率”的知识后提出了一个问题:“斜面的机械效率与斜面的倾斜程度有没有关系?”针对这个问题他做了在斜面上匀速拉动小车的探究实验,并记录实验数据如下:
斜需倾斜程度
小车重G/N
小车上升高试h/m
沿斜面拉力F/N
小车行色匆匆 动距离s/m
有用功W有/J
总功W W总/J
机械效率
较缓
10
0.1
3
1
1
3
33%
较陡
10
0.2
4
1
最陡
10
0.4
6
1
4
6
67%
请根据以上实验数据回答:
(1)“较陡”时,做的有用功为________,总功为________,机械效率为________
(2)通过对上述实验数据的分析,你对小周提出的问题可获得的初步结论是:________
(3)如果小周还想探究斜面的机械效率与物重的关系,实验时应该控制哪些条件不变?
四、计算题(共2题)
19.如图所示,工人用滑轮组提升重240N的物体,所用的拉力为150N,物体在5s内匀速上升1m。求:
(1)有用功;
(2)滑轮组的机械效率;
(3)拉力的功率。
20.如图所示的滑轮组将重12N的物体匀速提升。所用的拉力F=5N,求滑轮组的机械效率。若用该滑轮组提升18N的重物时,求所用的拉力。(忽略绳重和滑轮与轴的摩擦)
答案解析部分
一、单选题
1. C
解:利用水桶把水从水井提上来,对水做的功的有用功,对桶做的功是额外功,人做的功是总功,C符合题意。 故答案为:C. 【分析】人想要做的功的是有用功,人不想做又不得不做的功是额外功。
2. C
解:A、把桶中水提高做的功属于额外功;A不符合题意; B、手对绳子拉力做的功属于额外功;B不符合题意; C、把桶提高做的功属于有用功;C符合题意; D、提整个桶做的功属于总功;D不符合题意; 故答案为:C。
【分析】本题的目的是打捞水桶,所以对木桶做的功属于有用功。做功的两个必要因素:作用在物体上的力和物体在力的方向上通过的距离;有用功的定义:当一个力作用在物体上,并使物体在力的方向上通过了一段距离,力学中就说这个力对物体做了功;额外功是并非我们需要但又不得不额外做的功;额外功加有用功就是总功。
3. D
解:加润滑油后工人提升同样的重物时,物体的重力不变、提升高度不变(都提升到五楼),根据W有=Gh可知,有用功不变;但加了润滑油后,额外功变小,因总功等于有用功加上额外功,所以工人做的总功变小。
故答案为:D
【分析】根据W有=Gh可知有用功变化情况;但加了润滑油后,额外功变小,因总功等于有用功加上额外功,可知工人做的总功变化情况.
4. D
解:物体上升做的有用功为, 克服摩擦的额外功为, 总功为W=1.8J+0.36J=2.16J,拉力为, 机械效率为, D符合题意,ABC不符合题意。 故答案为:D.
【分析】根据物体的重力和高度的乘积计算有用功,利用摩擦力和长度计算额外功,利用总功和斜面长度计算拉力,有用功和总功的比值计算机械效率。
5. C
解:机械效率表示有用功和总功的比值大小,由于额外功的存在,机械效率小于100%,功率表做功的快慢,不是做功的多少,C符合题意。 故答案为:C. 【分析】机械效率是有用功和总功的比值,由于额外功的存在,机械效率小于100%,功率表做功的快慢。
6. C
解: AD、把同一物体匀速提升同样的高度,由W有用=Gh可知,前后两次做的有用功不变,此AD不符合题意;
BC、有用功一定,机械效率增加,由公式η= = 知:总功减小,额外功减小。C符合题意、B不符合题意。
故答案为:C。
【分析】结合W有用=Gh可知前后两次做的有用功不变,再结合公式η= = ?分析理解.
7. B
解: A、如图滑轮组,承担物重的绳子股数n=2,
不计绳重和摩擦,拉力F的大小:
F= (G物+G动)= ×(8N+2N)=5N,A符合题意;
B、绳子自由端移动距离:
s=2h=2×0.4m=0.8m,B不符合题意;
C、拉力F做的总功:
W总=Fs=5N×0.8m=4J,
拉力做功的功率:
P= = =2W,C符合题意;
D、使用滑轮组做的有用功:
W有用=Gh=8N×0.4m=3.2J,
滑轮组的机械效率:
η= = ×100%=80%,D符合题意。
故答案为:B。
【分析】利用W有用=Gh求出有用功.利用W总=Fs=Fnh求拉力做功;再利用功率公式P=求拉力做功的功率;利用 η=?计算滑轮组的机械效率.
8. D
解: AB、由题知,提起两物体所用的滑轮组相同,将物体提升相同的高度,不计绳重和摩擦,克服动滑轮重力所做的功是额外功,由W额=G动h知,提升A和B所做额外功相同,A、B不符合题意;
CD、不计绳重与摩擦的影响,滑轮组的机械效率:η= = ,额外功相同,提升A物体时滑轮组的机械效率较大,所以提升A物体所做的有用功较大,其总功较大,C不符合题意、D符合题意。
故答案为:D。
【分析】不计绳重及摩擦,利用相同的滑轮和绳子、提升相同的高度,做额外功相同;而总功等于有用功与额外功之和; 机械效率是有用功与总功的比值,据此分析解答即可.
9. D
解:将同一物体分别沿光滑斜面(无摩擦力)AB、AC以相同的速度,匀速拉到顶点A,拉力F1、F2对物体所做的功等于物体克服重力所做的功,而同一物体升高相同的高度克服重力做的功相同,故W1=W2;又因 ,W相同,AB>AC,所以F1<F2 , 再由 知,速度相同,F1<F2 , 则P1<P2.
故答案为:D.
【分析】斜面越长,越省力,利用物体的重力和上升的高度可以计算有用功,功和时间的比值计算功率。
10. D
解:A. B. 剪刀使用时,其转轴处会存在摩擦力,且剪刀为一杠杆,使用时,阻力臂是变化的,故不能确定阻力或动力的大小,AB不符合题意;
C. D. 机械效率为有用功与总功的比,机械效率为80%时,若作用在剪刀的动力做功1J,表示有0.8J 的功用于剪纸;另外0.2J 的功是克服摩擦做的额外功,C不符合题意,D符合题意;
故答案为:D。
【分析】机械效率是有用功和总功的比值.
二、填空题
11. 87.5%;增大 解:(1)动滑轮上承担重力的绳子有2段,那么动滑轮的机械效率为:; (2)根据机械效率可知:当物重G增大时,而动滑轮的重力G动不变时,滑轮组的机械效率增大。 【分析】(1)使用动滑轮提升重物时,对物体做有用功,对动滑轮做额外功,可根据计算机械效率; (2)动滑轮的机械效率还可根据计算;物重增大,即G增大,分析分数值的变化即可。
12. 25;80%
解:忽略绳重及摩擦,拉力F= (G+G动)= ×(40N+10N)=25N;动滑轮的机械效率:η= =80%。 故答案为:25;80%. 【分析】忽略绳重及摩擦,拉力F= (G+G动);再利用η= 求得动滑轮的机械效率.
13. 1500;80%
解:由图知n=3,则绳子自由端移动的距离:s=3h=3×2m=6m,
拉力做的总功:
W总=Fs=250N×6m=1500J;
工人做的有用功:
W有=Gh=600N×2m=1200J,
滑轮组的机械效率:
η= = ×100%=80%。
故答案为:1500;80%;
【分析】利用W总=Fs=Fnh求得拉力做的总功,再利用W有=Gh求得工人做的有用功,最后用η= 求得滑轮组的机械效率.
14. ;800;250;增加提升的物重
解:(1)人向下拉绳使重物升起,说明绳子最后绕过的是定滑轮,按此反向绕线,则绳子的起始端应系在定滑轮的挂钩上,如图所示:
;(2)他所做的有用功:
W有用=Gh=400N×2m=800J;(3)由图知n=2,拉力端移动距离s=2h,
滑轮组η= = = = ,
则工人的拉力:
F= = =250N;(4)要提高机械效率,要尽量减小额外功、增大有用功,可增大使用滑轮组提升的物重、在转轴上加润滑油、减轻动滑轮的自重等。
故答案为:如图所示;800; 250;增加提升的物重。
【分析】以人手为起点开始绕线,利用W有用=Gh求得有用功,利用η= = 求得工人的拉力.要提高机械效率,要尽量减小额外功、增大有用功,据此分析即可.
15. 80%
解:拉力做的有用功:
W有用=Gh=200N×0.6m=120J,
拉力做的总功:
W总=Fs=50N×3m=150J,
滑轮组的机械效率:
η= = ×100%=80%。
故答案为:80%。
【分析】利用W有用=Gh求得有用功,再利用W总=Fs求得拉力做的总功,最后利用η= 求得滑轮组的机械效率.
16. 600;800;160;100;75%???
解:由题知,斜面长s=2m,斜面高h=1m,物体重G=600N,推力F=400N;
有用功:W有用=Gh=600N×1m=600J,推力做的总功:W总=Fs=400N×2m=800J,
推力做的总功的功率:P= ?=160W;额外功:W额外=W总?W有用=800J?600J=200J,
由W额外=fs得摩擦力: f= =100N;斜面的机械效率:η= ?=75%
故答案为:600;800;160;100;75%. 【分析】提升重物做的功是有用功,克服摩擦力所做的功是额外功,推力做的功是总功,推力做的总功的功率是总功率,利用η= 计算斜面的机械效率.
?
三、实验探究题
17. (1)匀速;2.4;5;0.3;0.36;83.3% (2)减小
解:(1)①实验中要竖直向上匀速拉动弹簧测力计,弹簧测力计示数稳定,便于读数;
②图中弹簧测力计每一个大格代表1N,每一个小格代表0.2N,拉力大小为2.4N;
③由图可知承担物重的绳子股数n=3,则钩码上升的高度h= = =5cm;
④W有用=Gh=6N×0.05m=0.3J,
W总=Fs=2.4N×0.15m=0.36J;滑轮组的机械效率:η= = ×100%=83.3%。(2)取下2个钩码后,则所做的有用功减小,而额外功不变,所以有用功在总功所占的比例减小,则滑轮组的机械效率将减小。故答案为:(1)匀速;2.4;5;0.3;0.36;83.3%;(2)减小
【分析】(1)拉力做的功为总功,克服重力做的功为有用功,有用功除以总功即为机械效率; (2)结合第一问求解的机械效率的表达式分析求解即可。
18. (1)2J;4J;50% (2)在其他条件不变的情况下,斜面越陡,机械效率越高 (3)斜面的倾斜程度、斜面与物体接触面的粗糙程度
解:(1)“较陡”时,做的有用功W有用 =GH=10N×0.2m=2J , 总功W总=FS=4N×1m=4J , 机械效率; (2)分析表中的机械效率的值可以看出:在其他条件不变的情况下,斜面越陡,机械效率越高; (3)要探究斜面机械效率与物重的关系 , 需要使斜面的倾斜程度相同 , 同时控制小车上升的高度(或小车在斜面上移动的距离),而改变物体的重力。 故答案为:(1)2J ; 4J ; 50% ; (2)在其他条件不变的情况下,斜面越陡,机械效率越高;(3)斜面的倾斜程度、斜面与物体接触面的粗糙程度。 【分析】(1)结合表中的数据,利用公式W=Gh计算出有用功,利用公式W=Fs计算总功,再根据公式计算机械效率; (2)分析表格中数据 , 斜面的倾斜程度逐渐变大 , 比较机械效率的值,得出结论; (3)要探究斜面机械效率与物重的关系 , 需要使斜面的倾斜程度相同 , 同时控制小车上升的高度(或小车在斜面上移动的距离),而改变物体的重力 , 分别测量不同重力时斜面的机械效率 , 分析得出结论。
四、计算题
19. (1)解:W有=Gh=240N×1m=240J;
答:有用功为240J
(2)解:W总=FS=150N×2m=300J;
∴η= = =80%;
答:滑轮组的机械效率为80%
(3)解:P= = =60W;
答:拉力的功率为60W
【分析】(1)(2)拉力做的功为总功,克服重力做的功为有用功,有用功除以总功即为机械效率; (3)利用拉力作的功除以做功的时间即为功率。
20. 解:η=W有用/W总=Gh/Fs=G/nP=12N/(3×5N)=80%
G动=nF-G=3×5N-12N=3N
F=(G物+G动)/n=(18N+3N)/3=7N
【分析】根据拉力和物体的重力,结合滑轮组的绳子股数,可以计算机械效率的大小,根据拉力和物体的重力还可以计算动滑轮的重力,结合物体重力和动滑轮的重力计算总的拉力大小。
