沪教版数学七年级下册第14章《三角形》单元复习与小结课件(17张)
文档属性
| 名称 | 沪教版数学七年级下册第14章《三角形》单元复习与小结课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 547.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-10 15:41:52 | ||
图片预览




文档简介
(共17张PPT)
第14章《三角形》单元复习与小结
知识归纳
?知识点一 三角形三边之间的关系(课本73页)
?三角形任意两边的和大于第三边.
一般地,在三条线段中,如果两条较短线段的和大于第三条最长的线段,那么以这三条线段为边就能构成一个三角形;否则,它们不能构成三角形.
?三角形任意两边的差小于第三边.
思考题1:若一个三角形周长是48,则这个三角形的最长边c的取值范围是( )
(A)0<c<24 (B)0<c≤16 (C)16<c<24 (D)16≤ c<24
1-2a>8-3
1-2a<8+3
练习:
已知三角形的三边长分别为3,1-2a,8,求a的取值范围.
知识归纳
?知识点二 三角形的内角和性质(课本79页)
? 三角形的内角和等于180°.
?三角形的一个外角等于与它不相邻的两个内角的和.
?三角形的一个外角大于任何一个与它不相邻的内角.
?知识点三 三角形的外角性质 (课本81页)
?三角形的外角和等于360°.
?知识点四 三角形的外角和性质(课本83页)
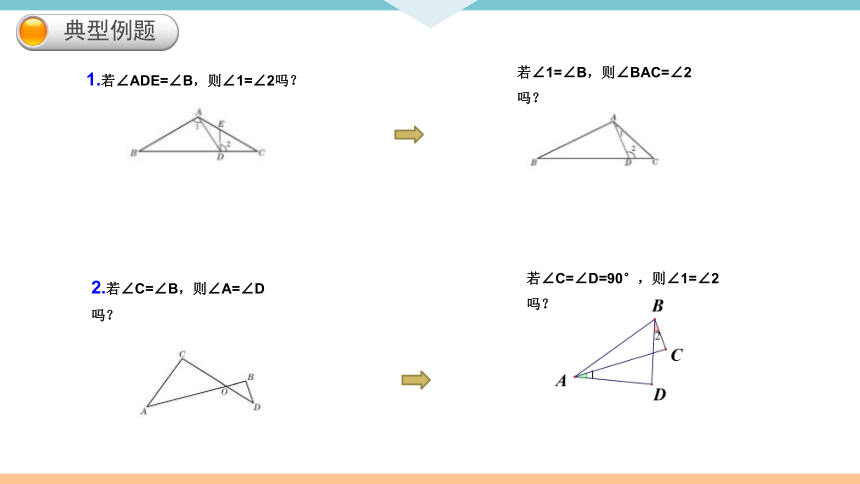
典型例题
若∠1=∠B,则∠BAC=∠2吗?
1.若∠ADE=∠B,则∠1=∠2吗?
2.若∠C=∠B,则∠A=∠D吗?
若∠C=∠D=90°,则∠1=∠2吗?
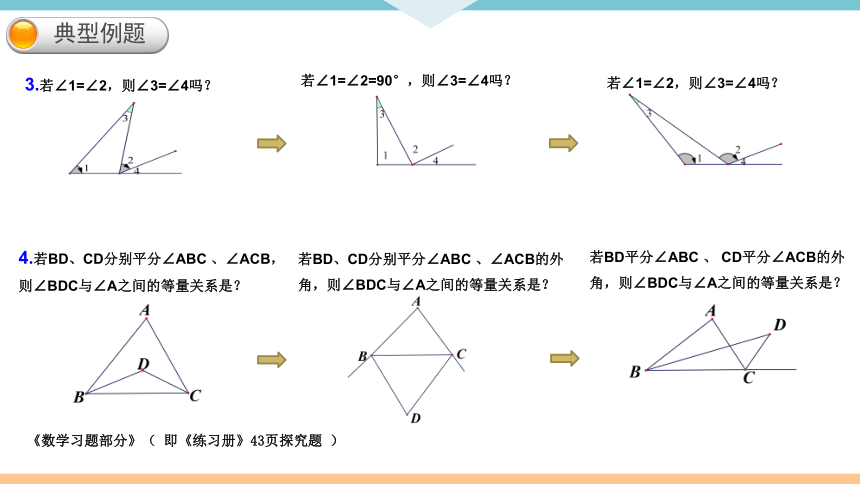
典型例题
3.若∠1=∠2,则∠3=∠4吗?
若∠1=∠2=90°,则∠3=∠4吗?
若∠1=∠2,则∠3=∠4吗?
4.若BD、CD分别平分∠ABC 、∠ACB,则∠BDC与∠A之间的等量关系是?
若BD、CD分别平分∠ABC 、∠ACB的外角,则∠BDC与∠A之间的等量关系是?
若BD平分∠ABC 、 CD平分∠ACB的外角,则∠BDC与∠A之间的等量关系是?
《数学习题部分》( 即《练习册》43页探究题 )
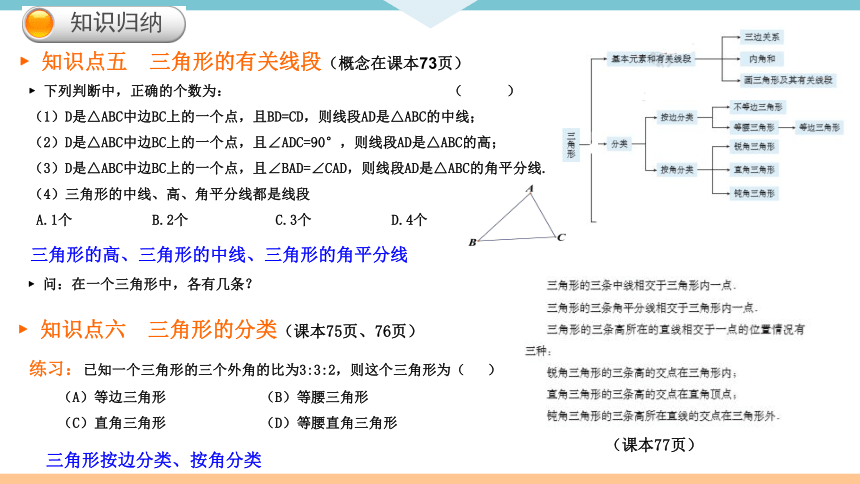
知识归纳
?知识点五 三角形的有关线段(概念在课本73页)
三角形的高、三角形的中线、三角形的角平分线
?问:在一个三角形中,各有几条?
?下列判断中,正确的个数为: ( )
(1)D是△ABC中边BC上的一个点,且BD=CD,则线段AD是△ABC的中线;
(2)D是△ABC中边BC上的一个点,且∠ADC=90°,则线段AD是△ABC的高;
(3)D是△ABC中边BC上的一个点,且∠BAD=∠CAD,则线段AD是△ABC的角平分线.
(4)三角形的中线、高、角平分线都是线段
A.1个 B.2个 C.3个 D.4个
?知识点六 三角形的分类(课本75页、76页)
练习:已知一个三角形的三个外角的比为3:3:2,则这个三角形为( )
(A)等边三角形 (B)等腰三角形
(C)直角三角形 (D)等腰直角三角形
(课本77页)
三角形按边分类、按角分类
典型例题
1.等腰三角形中的腰与底边:
分类讨论
1.若AB为腰,BC≠AB,则BC为底边,AC为腰,∴三边长分别为5,5,10,不能构成三角形,舍去
2.若AB为底边,BC≠AB,则BC、AC为腰, ∴三边长分别为5,10,10,能构成三角形,得到AC的长;
1.若AB为腰,BC≠AB, 则BC为?,AC为?,∴三边长分别为?此情况需要舍去吗?
2.若AB为底边,BC≠AB,则BC、AC为?, ∴三边长分别为?此情况需要舍去吗?
第(1)题
第(2)题
?
典型例题
2.等腰三角形中的顶角与底角:
已知一个等腰三角形中:
(1)若有一个角为100°,那么另外两个角的度数是多少?
(2)若有一个角为40° ,那么另外两个角的度数是多少?
第(1)题
1.若100°的角为底角,由三角形内角和以及底角的概念 可知,图形不存在,舍去
2.若100°的角为顶角,则另两个角为相等的两个底角,由三角形内角和可求出角度;
第(2)题
1.若40°的角为底角,则另两个角一个为底角,一个为顶角,由三角形内角和求出角度;
2.若40°的角为顶角,则另两个角为相等的底角,由三角形内角和可求出角度;
练习:等腰三角形的一个外角等于150°,则与它不相邻的两个内角的度数分别为多少?
分类讨论
顶角的外角
底角的外角
数形结合
典型例题
第(1)题
第(2)题
3.等腰三角形腰上的高:
已知一个等腰三角形:
(1)一腰上的高与另一腰的夹角为50°,那么底角的度数是多少?
(2)一腰上的高与底边的夹角为50°, 那么底角的度数是多少?
(3)一腰上的高与底边的夹角为40°, 那么底角的度数是多少?
第(3)题
(有两种情况)
(只有一种情况)
(只有一种情况)
分类讨论
数形结合
典型例题
知识归纳
?知识点七 全等三角形的判定方法
? SAS 、ASA、AAS、SSS
?知识点八 全等三角形的性质(课本87页)
? 全等三角形的对应边相等,对应角相等
?两个全等形,其中一个图形经过平移、旋转、翻折运动后,一定可以与另一个图形重合。
?两个全等三角形,经过运动后一定重合。
典型例题
1.课本101页:
已知:FD=DE,BF=CD,∠FDE=∠B,
试说明∠B=∠C
练习:
已知如图: ∠DEA=∠ECB=90°, ∠DAE=∠ABC, DE+AE=EC, 试判断 △BDA的形状,并说明理由.
课本99页:
已知:AB=AC, ∠D=∠E=90° ∠BAC=90°,试说明 △BDA与△AEC全等
典型例题
2.课本103页:
已知:CE=AB,AD⊥BC于点D,∠1=∠2,
试说明AD=DC.
课本103页:
已知:CE=CD,∠ACB=90°,CA=CB,
试说明AD=BE.
已知:在△ABC中,AB=AC,两条高AD和BE交于点H,且AE=BE,
试说明AH=2BD.
思考题2:
已知如图,在△ABC中,BC=AC, ∠ACB=90°,D在AC上,AE⊥BD的延长线于点E,且AE= BD,试说明BD平分∠ABC的理由.
典型例题
3.课本103页:
已知:∠1=∠2, AB=AC,AD=AE,
试说明∠D=∠E.
课本114页:
已知:点B、C、E在一直线上,△ABC △DCE都是等边三角形,联结AE、BD,试说明△ACE与△BCD全等的理由.
思考题3:
《数学练习部分》
即《练习册》64页第6题:
知识归纳
?知识点九 等腰三角形的判定与性质(课本105页至108页)
名称 性质与边角关系 判 定
等
腰
三
角
形
1.两腰相等
2.等边对等角
3. 三线合一
4.是轴对称图形
1.两边相等
2.等角对等边
知识归纳
?知识点十 等边三角形的判定与性质(课本112页、113页)
名称 性质与边角关系 判 定
等
边
三
角
形
1.三边都相等
2.每个内角等于60°
3. 三线合一
4.是轴对称图形,
(共有几条对称轴?)
1.三边都相等的三角形
2.三个内角都相等的三角形
3.有一个内角等于60°的等腰三角形
小结与作业
结束语:
1.《练习册》62页:复习题第1、2、3题,做在练习册上;
2.《练习册》63页:复习题第4题,做在本子上;
作业:
? 简单模仿 变式练习 自发领悟 自觉分析
选做:
思考题1:若一个三角形周长是48,则这个三角形的最长边c的取值范围是( )
(A)0<c<24 (B)0<c≤16 (C)16<c<24 (D)16≤ c<24
思考题2:
已知如图,在△ABC中,BC=AC, ∠ACB=90°,D在AC上,AE⊥BD的延长线于点E,且AE= BD,试说明BD平分∠ABC的理由.
思考题3:
《数学练习部分》即《练习册》64页第6题:
第14章《三角形》单元复习与小结
知识归纳
?知识点一 三角形三边之间的关系(课本73页)
?三角形任意两边的和大于第三边.
一般地,在三条线段中,如果两条较短线段的和大于第三条最长的线段,那么以这三条线段为边就能构成一个三角形;否则,它们不能构成三角形.
?三角形任意两边的差小于第三边.
思考题1:若一个三角形周长是48,则这个三角形的最长边c的取值范围是( )
(A)0<c<24 (B)0<c≤16 (C)16<c<24 (D)16≤ c<24
1-2a>8-3
1-2a<8+3
练习:
已知三角形的三边长分别为3,1-2a,8,求a的取值范围.
知识归纳
?知识点二 三角形的内角和性质(课本79页)
? 三角形的内角和等于180°.
?三角形的一个外角等于与它不相邻的两个内角的和.
?三角形的一个外角大于任何一个与它不相邻的内角.
?知识点三 三角形的外角性质 (课本81页)
?三角形的外角和等于360°.
?知识点四 三角形的外角和性质(课本83页)
典型例题
若∠1=∠B,则∠BAC=∠2吗?
1.若∠ADE=∠B,则∠1=∠2吗?
2.若∠C=∠B,则∠A=∠D吗?
若∠C=∠D=90°,则∠1=∠2吗?
典型例题
3.若∠1=∠2,则∠3=∠4吗?
若∠1=∠2=90°,则∠3=∠4吗?
若∠1=∠2,则∠3=∠4吗?
4.若BD、CD分别平分∠ABC 、∠ACB,则∠BDC与∠A之间的等量关系是?
若BD、CD分别平分∠ABC 、∠ACB的外角,则∠BDC与∠A之间的等量关系是?
若BD平分∠ABC 、 CD平分∠ACB的外角,则∠BDC与∠A之间的等量关系是?
《数学习题部分》( 即《练习册》43页探究题 )
知识归纳
?知识点五 三角形的有关线段(概念在课本73页)
三角形的高、三角形的中线、三角形的角平分线
?问:在一个三角形中,各有几条?
?下列判断中,正确的个数为: ( )
(1)D是△ABC中边BC上的一个点,且BD=CD,则线段AD是△ABC的中线;
(2)D是△ABC中边BC上的一个点,且∠ADC=90°,则线段AD是△ABC的高;
(3)D是△ABC中边BC上的一个点,且∠BAD=∠CAD,则线段AD是△ABC的角平分线.
(4)三角形的中线、高、角平分线都是线段
A.1个 B.2个 C.3个 D.4个
?知识点六 三角形的分类(课本75页、76页)
练习:已知一个三角形的三个外角的比为3:3:2,则这个三角形为( )
(A)等边三角形 (B)等腰三角形
(C)直角三角形 (D)等腰直角三角形
(课本77页)
三角形按边分类、按角分类
典型例题
1.等腰三角形中的腰与底边:
分类讨论
1.若AB为腰,BC≠AB,则BC为底边,AC为腰,∴三边长分别为5,5,10,不能构成三角形,舍去
2.若AB为底边,BC≠AB,则BC、AC为腰, ∴三边长分别为5,10,10,能构成三角形,得到AC的长;
1.若AB为腰,BC≠AB, 则BC为?,AC为?,∴三边长分别为?此情况需要舍去吗?
2.若AB为底边,BC≠AB,则BC、AC为?, ∴三边长分别为?此情况需要舍去吗?
第(1)题
第(2)题
?
典型例题
2.等腰三角形中的顶角与底角:
已知一个等腰三角形中:
(1)若有一个角为100°,那么另外两个角的度数是多少?
(2)若有一个角为40° ,那么另外两个角的度数是多少?
第(1)题
1.若100°的角为底角,由三角形内角和以及底角的概念 可知,图形不存在,舍去
2.若100°的角为顶角,则另两个角为相等的两个底角,由三角形内角和可求出角度;
第(2)题
1.若40°的角为底角,则另两个角一个为底角,一个为顶角,由三角形内角和求出角度;
2.若40°的角为顶角,则另两个角为相等的底角,由三角形内角和可求出角度;
练习:等腰三角形的一个外角等于150°,则与它不相邻的两个内角的度数分别为多少?
分类讨论
顶角的外角
底角的外角
数形结合
典型例题
第(1)题
第(2)题
3.等腰三角形腰上的高:
已知一个等腰三角形:
(1)一腰上的高与另一腰的夹角为50°,那么底角的度数是多少?
(2)一腰上的高与底边的夹角为50°, 那么底角的度数是多少?
(3)一腰上的高与底边的夹角为40°, 那么底角的度数是多少?
第(3)题
(有两种情况)
(只有一种情况)
(只有一种情况)
分类讨论
数形结合
典型例题
知识归纳
?知识点七 全等三角形的判定方法
? SAS 、ASA、AAS、SSS
?知识点八 全等三角形的性质(课本87页)
? 全等三角形的对应边相等,对应角相等
?两个全等形,其中一个图形经过平移、旋转、翻折运动后,一定可以与另一个图形重合。
?两个全等三角形,经过运动后一定重合。
典型例题
1.课本101页:
已知:FD=DE,BF=CD,∠FDE=∠B,
试说明∠B=∠C
练习:
已知如图: ∠DEA=∠ECB=90°, ∠DAE=∠ABC, DE+AE=EC, 试判断 △BDA的形状,并说明理由.
课本99页:
已知:AB=AC, ∠D=∠E=90° ∠BAC=90°,试说明 △BDA与△AEC全等
典型例题
2.课本103页:
已知:CE=AB,AD⊥BC于点D,∠1=∠2,
试说明AD=DC.
课本103页:
已知:CE=CD,∠ACB=90°,CA=CB,
试说明AD=BE.
已知:在△ABC中,AB=AC,两条高AD和BE交于点H,且AE=BE,
试说明AH=2BD.
思考题2:
已知如图,在△ABC中,BC=AC, ∠ACB=90°,D在AC上,AE⊥BD的延长线于点E,且AE= BD,试说明BD平分∠ABC的理由.
典型例题
3.课本103页:
已知:∠1=∠2, AB=AC,AD=AE,
试说明∠D=∠E.
课本114页:
已知:点B、C、E在一直线上,△ABC △DCE都是等边三角形,联结AE、BD,试说明△ACE与△BCD全等的理由.
思考题3:
《数学练习部分》
即《练习册》64页第6题:
知识归纳
?知识点九 等腰三角形的判定与性质(课本105页至108页)
名称 性质与边角关系 判 定
等
腰
三
角
形
1.两腰相等
2.等边对等角
3. 三线合一
4.是轴对称图形
1.两边相等
2.等角对等边
知识归纳
?知识点十 等边三角形的判定与性质(课本112页、113页)
名称 性质与边角关系 判 定
等
边
三
角
形
1.三边都相等
2.每个内角等于60°
3. 三线合一
4.是轴对称图形,
(共有几条对称轴?)
1.三边都相等的三角形
2.三个内角都相等的三角形
3.有一个内角等于60°的等腰三角形
小结与作业
结束语:
1.《练习册》62页:复习题第1、2、3题,做在练习册上;
2.《练习册》63页:复习题第4题,做在本子上;
作业:
? 简单模仿 变式练习 自发领悟 自觉分析
选做:
思考题1:若一个三角形周长是48,则这个三角形的最长边c的取值范围是( )
(A)0<c<24 (B)0<c≤16 (C)16<c<24 (D)16≤ c<24
思考题2:
已知如图,在△ABC中,BC=AC, ∠ACB=90°,D在AC上,AE⊥BD的延长线于点E,且AE= BD,试说明BD平分∠ABC的理由.
思考题3:
《数学练习部分》即《练习册》64页第6题:
