人教版六年级下册数学 3.圆柱的体积课件( 共17张PPT)
文档属性
| 名称 | 人教版六年级下册数学 3.圆柱的体积课件( 共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-10 06:36:25 | ||
图片预览



文档简介
(共17张PPT)
圆柱的体积
教学目标
1、通过创设生活情境,使学生在解决
简单实际问题的过程中掌握圆柱体积的
计算方法。
2、通过探索新知,培养学生解决问题的能力。
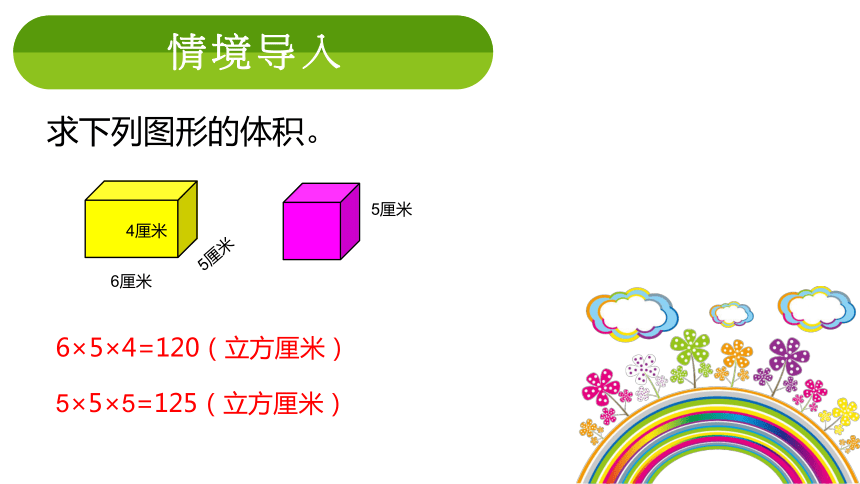
情境导入
求下列图形的体积。
5厘米
6厘米
5厘米
4厘米
6×5×4=120(立方厘米)
5×5×5=125(立方厘米)
情境导入
长方体的体积公式
正方体的体积公式
长方体的体积=长×宽×高
=底面积×高
正方体的体积=棱长×棱长×棱长
=底面积×高
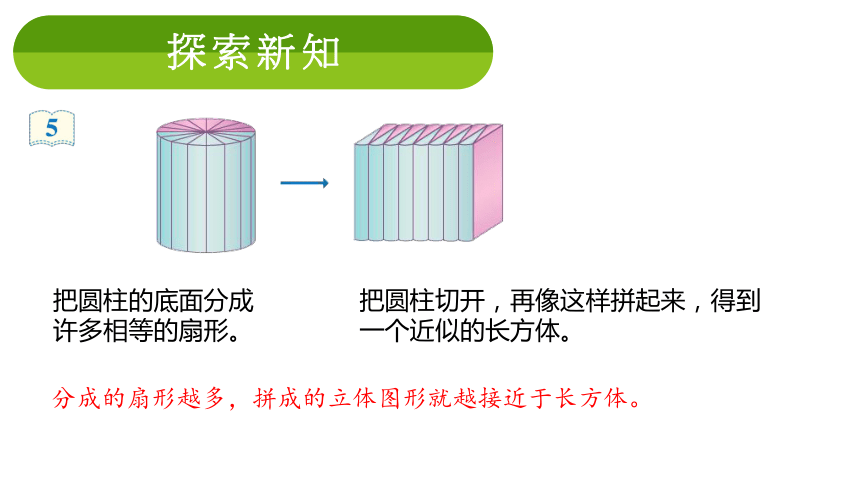
探索新知
把圆柱的底面分成
许多相等的扇形。
分成的扇形越多,拼成的立体图形就越接近于长方体。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
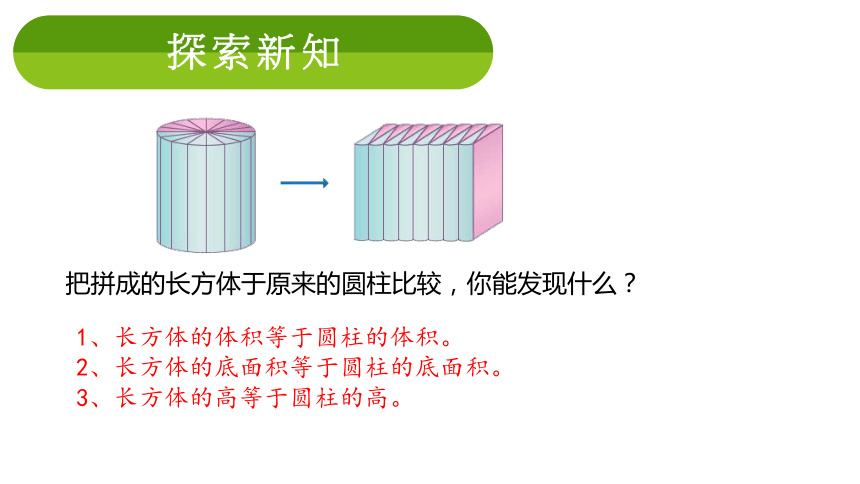
探索新知
把拼成的长方体于原来的圆柱比较,你能发现什么?
1、长方体的体积等于圆柱的体积。
2、长方体的底面积等于圆柱的底面积。
3、长方体的高等于圆柱的高。
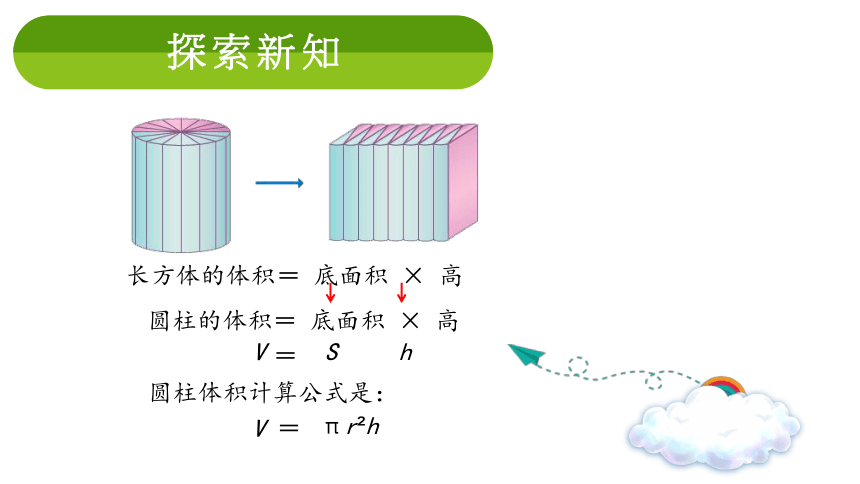
探索新知
圆柱体积计算公式是:
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
=
S
h
πr?h
V
=
探索新知
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
要想回答这个问题,先要计算出杯子的容积。
要回答这个问题,先要计算什么?
探索新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的
容积是多少?
瓶子里水的体积倒置后没变,水的体积加上18cm高圆柱的体积就是瓶子的容积。也就是
把瓶子的容积转化成了两个圆柱的容积。
这个瓶子是完整的圆柱吗?能不能转化成圆柱呢?
利用体积不变的特性,把不规则图形转化成规则图形来计算。
课堂小结
圆柱体积计算公式是:
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
=
S
h
πr?h
V
=
底面
底面
高
利用体积不变的特性,把不规则图形转化成规则图形来计算。
学以致用
1. 一个圆柱的体积是80cm?,底面积是16cm2。它的高是多少厘米?
80 ÷16 =5(cm)
答:它的高是5cm。
学以致用
2. 一个酸奶瓶,它的瓶身呈圆柱形(不包括瓶颈),底面半径4厘米,当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
3.14×42×8=401.92(立方厘米)
答:瓶内酸奶体积是401.92立方厘米。
学以致用
3.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,
无水部分高10厘米,内直径是6厘米。小明喝了多少毫升水?
3.14×(6÷2)2×10=282.6(立方厘米)=282.6毫升
答:小明喝了282.6毫升水。
学以致用
答:小明喝了282.6毫升水。
3.14×(10÷2)2×2=157(立方厘米)
4、一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2cm,求这块铁块的体积。
学以致用
学以致用
5、把一块长31.4cm、宽20cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
答:圆柱的高是50厘米。
31.4×20×4÷(3.14×42)=50(厘米)
作业
练习题19
THANKS !
下课啦!
圆柱的体积
教学目标
1、通过创设生活情境,使学生在解决
简单实际问题的过程中掌握圆柱体积的
计算方法。
2、通过探索新知,培养学生解决问题的能力。
情境导入
求下列图形的体积。
5厘米
6厘米
5厘米
4厘米
6×5×4=120(立方厘米)
5×5×5=125(立方厘米)
情境导入
长方体的体积公式
正方体的体积公式
长方体的体积=长×宽×高
=底面积×高
正方体的体积=棱长×棱长×棱长
=底面积×高
探索新知
把圆柱的底面分成
许多相等的扇形。
分成的扇形越多,拼成的立体图形就越接近于长方体。
把圆柱切开,再像这样拼起来,得到一个近似的长方体。
探索新知
把拼成的长方体于原来的圆柱比较,你能发现什么?
1、长方体的体积等于圆柱的体积。
2、长方体的底面积等于圆柱的底面积。
3、长方体的高等于圆柱的高。
探索新知
圆柱体积计算公式是:
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
=
S
h
πr?h
V
=
探索新知
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
要想回答这个问题,先要计算出杯子的容积。
要回答这个问题,先要计算什么?
探索新知
一个内直径是8cm的瓶子里,水的高度是7cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度是18cm。这个瓶子的
容积是多少?
瓶子里水的体积倒置后没变,水的体积加上18cm高圆柱的体积就是瓶子的容积。也就是
把瓶子的容积转化成了两个圆柱的容积。
这个瓶子是完整的圆柱吗?能不能转化成圆柱呢?
利用体积不变的特性,把不规则图形转化成规则图形来计算。
课堂小结
圆柱体积计算公式是:
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V
=
S
h
πr?h
V
=
底面
底面
高
利用体积不变的特性,把不规则图形转化成规则图形来计算。
学以致用
1. 一个圆柱的体积是80cm?,底面积是16cm2。它的高是多少厘米?
80 ÷16 =5(cm)
答:它的高是5cm。
学以致用
2. 一个酸奶瓶,它的瓶身呈圆柱形(不包括瓶颈),底面半径4厘米,当瓶子正放时,瓶内酸奶高为8厘米,瓶子倒放时,空余部分高为2厘米.请你算一算,瓶内酸奶体积是多少立方厘米?
3.14×42×8=401.92(立方厘米)
答:瓶内酸奶体积是401.92立方厘米。
学以致用
3.一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,
无水部分高10厘米,内直径是6厘米。小明喝了多少毫升水?
3.14×(6÷2)2×10=282.6(立方厘米)=282.6毫升
答:小明喝了282.6毫升水。
学以致用
答:小明喝了282.6毫升水。
3.14×(10÷2)2×2=157(立方厘米)
4、一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸在这个容器的水中的铁块取出后,水面下降2cm,求这块铁块的体积。
学以致用
学以致用
5、把一块长31.4cm、宽20cm、高4cm的长方体钢坯熔铸成底面半径是4cm的圆柱,圆柱的高是多少厘米?
答:圆柱的高是50厘米。
31.4×20×4÷(3.14×42)=50(厘米)
作业
练习题19
THANKS !
下课啦!
