2019-2020学年高中数学新同步苏教版必修1学案:模块复习课Word版含解析
文档属性
| 名称 | 2019-2020学年高中数学新同步苏教版必修1学案:模块复习课Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 175.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-12 00:00:00 | ||
图片预览


文档简介
1.集合
(1)集合元素的特性:确定性、互异性、无序性.
(2)子集:对任意的x∈A,有x∈B,则A?B(或B?A).
(3)真子集:若A?B,且A≠B,则AB(或BA).
(4)集合的运算及其性质
并集:A∪B={x|x∈A,或x∈B};
交集:A∩B={x|x∈A,且x∈B};
补集:?UA={x|x∈U,且x?A}.
(5)集合的运算性质
①并集的性质:A∪?=A;A∪A=A;A∪B=A?B?A.
②交集的性质:A∩?=?;A∩A=A;A∩B=A?A?B.
③补集的性质:A∪(?UA)=U;A∩(?UA)=?;?U(?UA)=A.
2.函数
(1)函数的三要素:定义域、值域、对应关系.
(2)分段函数:在定义域内不同部分上,有不同的解析表达式,像这样的函数通常叫做分段函数.
3.函数的性质
(1)单调性
设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量x1,x2,当x1<x2时,
①若f(x1)<f(x2),则f(x)在区间D上是增函数;
②若f(x1)>f(x2),则f(x)在区间D上是减函数.
(2)奇偶性
①一般地,设函数y=f(x)的定义域为A,如果对于任意的x∈A,都有f(-x)=f(x),那么称函数y=f(x)是偶函数.
②如果对于任意的x∈A,都有f(-x)=-f(x),那么称函数y=f(x)是奇函数.
③奇函数的图象关于原点对称;偶函数的图象关于y轴对称.
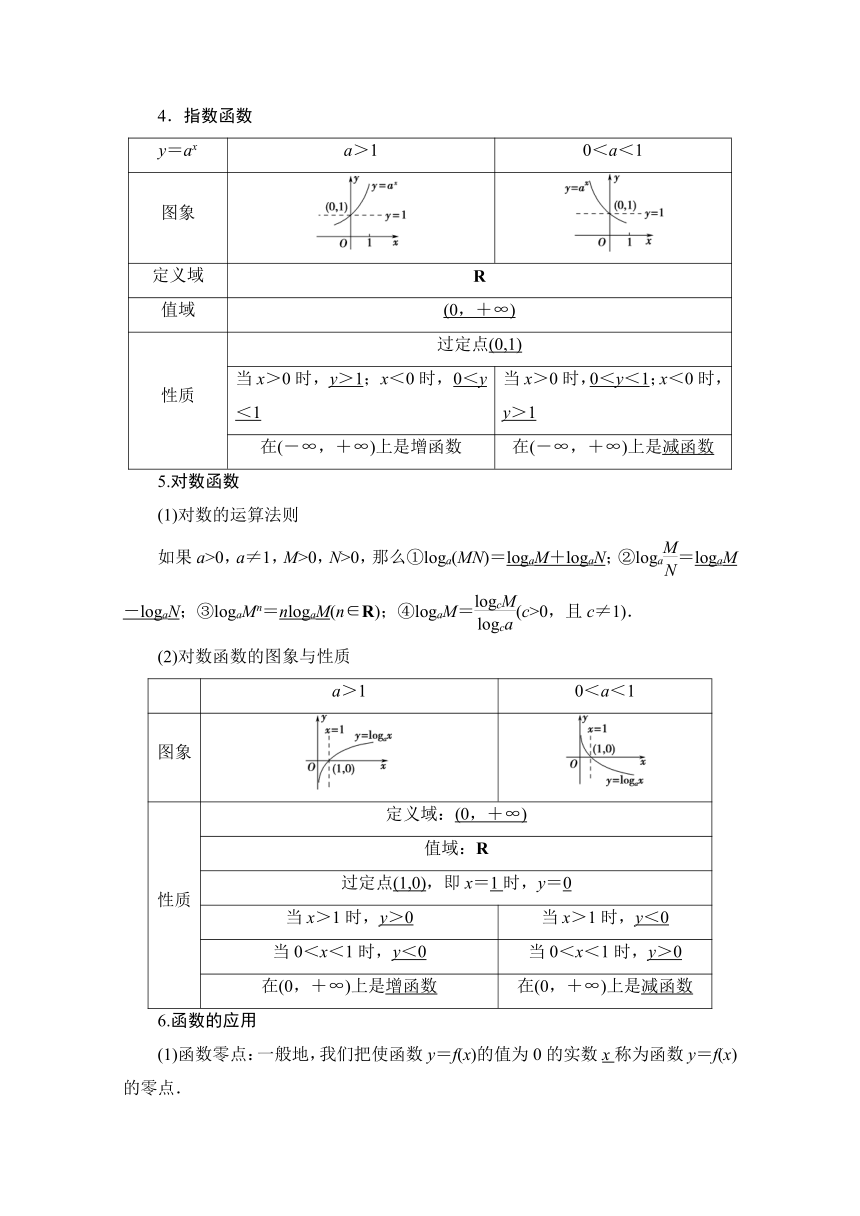
4.指数函数
y=ax
a>1
0<a<1
图象
定义域
R
值域
(0,+∞)
性质
过定点(0,1)
当x>0时,y>1;x<0时,0<y<1
当x>0时,0<y<1;x<0时,y>1
在(-∞,+∞)上是增函数
在(-∞,+∞)上是减函数
5.对数函数
(1)对数的运算法则
如果a>0,a≠1,M>0,N>0,那么①loga(MN)=logaM+logaN;②loga=logaM-logaN;③logaMn=nlogaM(n∈R);④logaM=(c>0,且c≠1).
(2)对数函数的图象与性质
a>1
0<a<1
图象
性质
定义域:(0,+∞)
值域:R
过定点(1,0),即x=1时,y=0
当x>1时,y>0
当x>1时,y<0
当0<x<1时,y<0
当0<x<1时,y>0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
6.函数的应用
(1)函数零点:一般地,我们把使函数y=f(x)的值为0的实数x称为函数y=f(x)的零点.
(2)方程f(x)=0有实数根?函数y=f(x)的图象与x轴有交点?函数y=f(x)有零点.
(3)函数零点的判定(零点存在性定理):如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是f(x)=0的根.
1.高一四班的全体同学组成一个集合. (√)
2.集合{-5,-8}和{(-5,-8)}表示同一个集合. (×)
[提示] {-5,-8}表示由两个元素-5和-8组成的集合,而{(-5,-8)}表示由一个元素(-5,-8)组成的集合.
3.若A?B,则A中的元素都在B中. (√)
4.若A∩B=A∩C,则必有B=C. (×)
[提示] A和B的公共元素与A和C的公共元素相同时A∩B=A∩C,但B和C不一定相等.
5.A∩?UA=?. (√)
6.若函数的定义域只有一个元素,则值域也只有一个元素. (√)
7.函数的图象一定是定义区间上一条连续不断的曲线. (×)
[提示] 函数图象不一定连续,也不一定是曲线.
8.分段函数由几个函数构成. (×)
[提示] 分段函数是一个函数.
9.所有的函数在其定义域上都具有单调性. (×)
[提示] 只有少数函数在其定义域上具有单调性.
10.任何函数都有最大值或最小值. (×)
[提示] 一次函数等就没有最值.
11.函数的最小值一定比最大值小. (√)
12.奇、偶函数的定义域都关于原点对称. (√)
13.若f(x)是奇函数,则f(-x)+f(x)=0. (√)
14.指数函数的图象一定在x轴的上方. (√)
15.函数y=2-x的定义域为{x|x≠0}. (×)
[提示] y=2-x的定义域为R.
16.对数运算的实质是求幂指数. (√)
17.loga=. (×)
[提示] loga=logaM-logaN.
18.当0<a<1时,若x>1,则y=logax的函数值都大于零. (×)
[提示] 题中函数值都小于零.
19.函数y=log2x与y=x2互为反函数. (×)
[提示] 函数y=log2x与y=2x互为反函数.
20.二次函数都是幂函数. (×)
[提示] 二次函数中只有y=x2是幂函数.
21.函数的零点是一个点. (×)
[提示] 函数的零点是函数值等于0时的自变量值,是一个数.
22.若函数y=f(x)在区间(a,b)上有零点,则一定有f(a)·f(b)<0. (×)
[提示] 函数在(a,b)上有零点,f(a)·f(b)的值不能确定,可为正数也可能为负数或者是0.
23.函数f(x)=|x|可以用二分法求其零点. (×)
[提示] f(x)=|x|在零点x=0的西侧函数组都是正的,不能用二分法求零点.
24.在一次函数模型中,系数k的取值会影响函数的性质. (√)
25.当a>1,n>0时,在区间(0,+∞)上,对任意的x,总有logax
27.0的任何指数幂都等于0. (×)
[提示] 0的任何非零指数幂等于0.
28.y=log2x2与y=logx3都不是对数函数. (√)
29.y=f(-x)的图象与y=f(x)的图象关于y轴对称. (√)
30.函数的定义域、值域确定后,对应法则就确定了. (×)
[提示] 函数的定义域、值域确定后,对应法则可以不同.如定义域、值域都是[0,1],对应法则可以为y=x或y=x2.
1.(2018·全国卷Ⅰ)已知集合A={x|x2-x-2>0},则?RA=( )
A.{x|-1<x<2} B.{x|-1≤x≤2}
C.{x|x<-1}∪{x|x>2} D.{x|x≤-1}∪{x|x≥2}
B [法一:A={x|(x-2)(x+1)>0}={x|x<-1或x>2},所以?RA={x|-1≤x≤2},故选B.
法二:因为A={x|x2-x-2>0},所以?RA={x|x2-x-2≤0}={x|-1≤x≤2},故选B.]
2.(2018·全国卷Ⅱ)已知集合A={(x,y)|x2+y2≤3,x∈Z,y∈Z},则A中元素的个数为( )
A.9 B.8 C.5 D.4
A [将满足x2+y2≤3的整数x,y全部列举出来,即(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)共有9个.]
3.(2018·全国卷Ⅲ)已知集合A={x|x-1≥0},B={0,1,2},则A∩B=( )
A.{0} B.{1}
C.{1,2} D.{0,1,2}
C [由题意知,A={x|x≥1},则A∩B={1,2}.]
4.(2018·全国卷Ⅰ)已知函数f(x)=g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是( )
A.[-1,0) B.[0,+∞)
C.[-1,+∞) D.[1,+∞)
C [函数g(x)=f(x)+x+a存在2个零点,即关于x的方程f(x)=-x-a有2个不同的实根,即函数f(x)的图象与直线y=-x-a有2个交点,作出直线y=-x-a与函数f(x)的图象,如图所示,
由图可知,-a≤1,解得a≥-1,故选C.]
5.(2018·全国卷Ⅱ)函数f(x)=的图象大致为( )
B [当x<0时,因为ex-e-x<0,所以此时f(x)=<0,故排除A、D;又f(1)=e->2,故排除C,选B.]
