湘教版九上数学2.3一元二次方程根的判别式 习题课件(26张)
文档属性
| 名称 | 湘教版九上数学2.3一元二次方程根的判别式 习题课件(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 741.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-11 12:00:30 | ||
图片预览








文档简介
(共26张PPT)
XJ版九年级上
2.3 一元二次方程根的判别式
第2章 一元二次方程
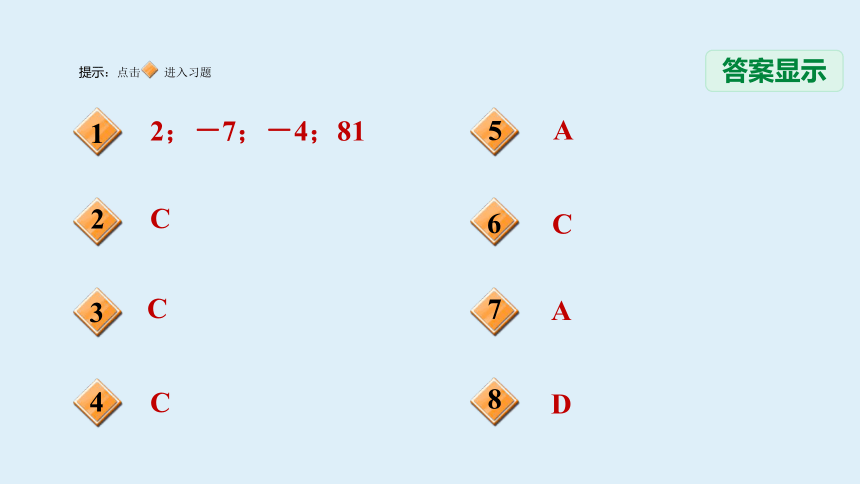
答案显示
2;-7;-4;81
C
C
C
A
C
D
A
答案显示
A
A
D
见习题
见习题
见习题
A
见习题
1.方程7x=2x2-4化为一般形式ax2+bx+c=0后,a=______,b=______,c=______,b2-4ac=______.
2
-7
-4
81
2.方程6x-8=5x2化为一般形式ax2+bx+c=0后,a,b,c的值为( )
A.a=5,b=6,c=-8
B.a=5,b=-6,c=-8
C.a=5,b=-6,c=8
D.a=6,b=5,c=8
C
3.在方程2x2+3x=1中,b2-4ac的值为( )
A.1 B.-1 C.17 D.-17
C
C
5.【中考·河南】一元二次方程(x+1)(x-1)=2x+3的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
A
6.【中考·湘西州】一元二次方程x2-2x+3=0根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断
C
*7.【中考·娄底】关于x的一元二次方程x2-(k+3)x+k=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.不能确定
【答案】A
【点拨】Δ=(k+3)2-4k=k2+2k+9=(k+1)2+8.
∵(k+1)2≥0,
∴(k+1)2+8>0,即Δ>0.
∴方程有两个不相等的实数根.
8.【中考·自贡】关于x的一元二次方程x2-2x+m=0无实数根,则实数m的取值范围是( )
A.m<1 B.m≥1 C.m≤1 D.m>1
D
9.【中考·荆州】若一次函数y=kx+b的图象不经过第二象限,则关于x的方程x2+kx+b=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
A
10.【中考·安徽】若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A.-1 B.1
C.-2或2 D.-3或1
【点拨】原方程可变形为x2+(a+1)x=0.
∵该方程有两个相等的实数根,
∴Δ=(a+1)2-4×1×0=0,解得a=-1.
A
*11.【中考·河北】小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c比原方程的c值小2,则原方程的根的情况是( )
A.不存在实数根
B.有两个不相等的实数根
C.有一个根是x=-1
D.有两个相等的实数根
【点拨】∵小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1,∴(-1)2-4+c=0,解得c=3,故原方程中c=5,则b2-4ac=16-4×1×5=-4<0,故原方程不存在实数根.
【答案】A
D
13.【中考·北京】关于x的方程x2-2x+2m-1=0有实数根,且m为正整数,求m的值及此时方程的根.
解:∵关于x的方程x2-2x+2m-1=0有实数根,
∴b2-4ac=4-4(2m-1)≥0,解得m≤1.
∵m为正整数,∴m=1,∴原方程为x2-2x+1=0,
则(x-1)2=0,解得x1=x2=1.
14.【中考·衡阳】关于x的一元二次方程x2-3x+k=0有实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程(m-1)x2+x+m-3=0与方程x2-3x+k=0有一个相同的根,求此时m的值.
(2)若等腰三角形ABC的一边长a=4,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.
解:2?5=2×5+5=15.
2?(-5)=2×(-5)+(-5)=-15.
XJ版九年级上
2.3 一元二次方程根的判别式
第2章 一元二次方程
答案显示
2;-7;-4;81
C
C
C
A
C
D
A
答案显示
A
A
D
见习题
见习题
见习题
A
见习题
1.方程7x=2x2-4化为一般形式ax2+bx+c=0后,a=______,b=______,c=______,b2-4ac=______.
2
-7
-4
81
2.方程6x-8=5x2化为一般形式ax2+bx+c=0后,a,b,c的值为( )
A.a=5,b=6,c=-8
B.a=5,b=-6,c=-8
C.a=5,b=-6,c=8
D.a=6,b=5,c=8
C
3.在方程2x2+3x=1中,b2-4ac的值为( )
A.1 B.-1 C.17 D.-17
C
C
5.【中考·河南】一元二次方程(x+1)(x-1)=2x+3的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
A
6.【中考·湘西州】一元二次方程x2-2x+3=0根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.无法判断
C
*7.【中考·娄底】关于x的一元二次方程x2-(k+3)x+k=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.不能确定
【答案】A
【点拨】Δ=(k+3)2-4k=k2+2k+9=(k+1)2+8.
∵(k+1)2≥0,
∴(k+1)2+8>0,即Δ>0.
∴方程有两个不相等的实数根.
8.【中考·自贡】关于x的一元二次方程x2-2x+m=0无实数根,则实数m的取值范围是( )
A.m<1 B.m≥1 C.m≤1 D.m>1
D
9.【中考·荆州】若一次函数y=kx+b的图象不经过第二象限,则关于x的方程x2+kx+b=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.无实数根
D.无法确定
A
10.【中考·安徽】若关于x的一元二次方程x(x+1)+ax=0有两个相等的实数根,则实数a的值为( )
A.-1 B.1
C.-2或2 D.-3或1
【点拨】原方程可变形为x2+(a+1)x=0.
∵该方程有两个相等的实数根,
∴Δ=(a+1)2-4×1×0=0,解得a=-1.
A
*11.【中考·河北】小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1.他核对时发现所抄的c比原方程的c值小2,则原方程的根的情况是( )
A.不存在实数根
B.有两个不相等的实数根
C.有一个根是x=-1
D.有两个相等的实数根
【点拨】∵小刚在解关于x的方程ax2+bx+c=0(a≠0)时,只抄对了a=1,b=4,解出其中一个根是x=-1,∴(-1)2-4+c=0,解得c=3,故原方程中c=5,则b2-4ac=16-4×1×5=-4<0,故原方程不存在实数根.
【答案】A
D
13.【中考·北京】关于x的方程x2-2x+2m-1=0有实数根,且m为正整数,求m的值及此时方程的根.
解:∵关于x的方程x2-2x+2m-1=0有实数根,
∴b2-4ac=4-4(2m-1)≥0,解得m≤1.
∵m为正整数,∴m=1,∴原方程为x2-2x+1=0,
则(x-1)2=0,解得x1=x2=1.
14.【中考·衡阳】关于x的一元二次方程x2-3x+k=0有实数根.
(1)求k的取值范围;
(2)如果k是符合条件的最大整数,且一元二次方程(m-1)x2+x+m-3=0与方程x2-3x+k=0有一个相同的根,求此时m的值.
(2)若等腰三角形ABC的一边长a=4,另两边长b,c恰好是这个方程的两个根,求△ABC的周长.
解:2?5=2×5+5=15.
2?(-5)=2×(-5)+(-5)=-15.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
