人教版数学八年级下册:17.1勾股定理(第二课时)课件 17PPT
文档属性
| 名称 | 人教版数学八年级下册:17.1勾股定理(第二课时)课件 17PPT |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-10 15:19:44 | ||
图片预览





文档简介
(共17张PPT)
在直角三角形ABC中,∠C=900 ,边BC、AC、AB所对应的边分别为a、b、c则存在下列关系,
勾股定理:
直角三角形中,两条直角边的平方和,等于斜边的平方。
a2+b2=c2
公式变形更常用:
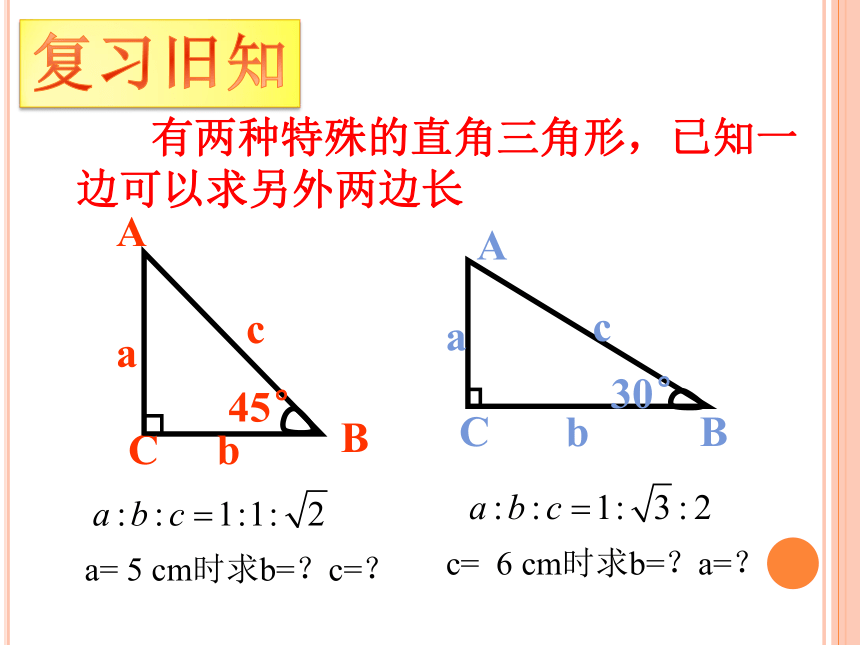
有两种特殊的直角三角形,已知一边可以求另外两边长
a= 5 cm时求b=?c=?
c= 6 cm时求b=?a=?
勾股小常识:勾股数
1、 基本勾股数如:大家一定要熟记
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
如:
6、8、10 ; 9、12、15
10、24、26 ; 15、36、39
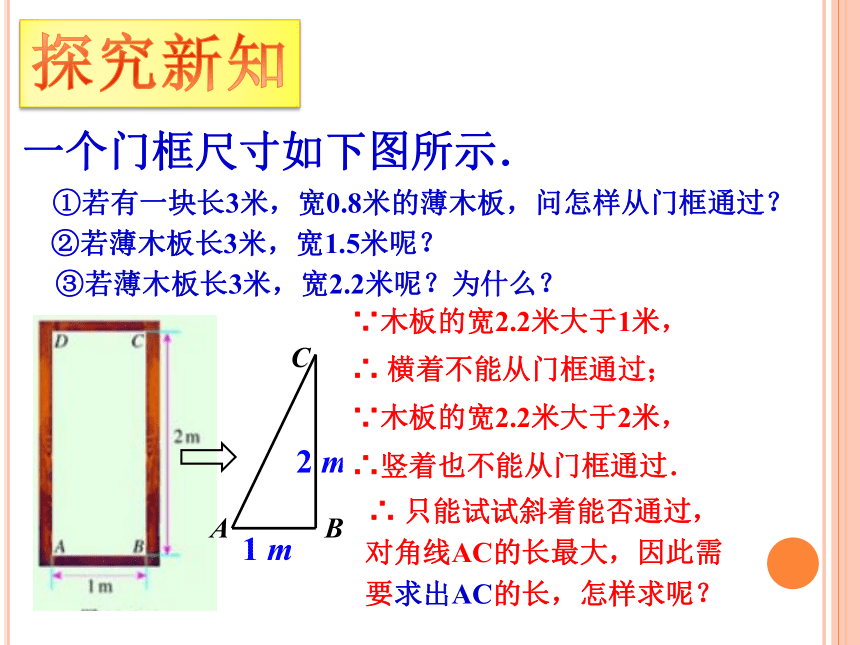
一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
1 m
2 m
∵木板的宽2.2米大于1米,
∴ 横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.
∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?
有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,
∴由勾股定理可知:
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数)
变式:以上题为背景,请同学们再设计其他方案构造直角三角形(或其他几何图形),测量池塘的长AB.
一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
D
E
解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.52
∴BC=0.7m
由题意得:DE=AB=2.5m
DC=AC-AD=2.4-0.4=2m
在Rt△DCE中,
∴BE=1.5-0.7=0.8m≠0.4m
答;梯子底端B不是外移0.4m
∵∠DCE=90 °
∴ DC2+ CE2=DE2
22+ BC2=2.52
∴CE=1.5m
如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
①求梯子的底端B距墙角O多少米?
②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:
猜一猜,底端也将滑动0.5米吗?
算一算,底端滑动的距离近似值是多少? (结果保留两位小数)
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
x
25-x
解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 ∵ DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
答:E站应建在离A站10km处。
∴ X=10
则 BE=(25-x)km
15
10
1、在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
解:设水池的深度AC为X尺,
则芦苇高AD为 (X+1)尺.
根据题意得:BC2+AC2=AB2
∴52+X2 =(X+1)2
25+X2=X2+2X+1
解得:X=12
∴X+1=12+1=13(尺)
答:水池的深度为12尺,芦苇高为13尺.
2、矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
解:设DE为X,
X
(8- X)
则CE为 (8- X).
由题意可知:EF=DE=X,
X
AF=AD=10
10
10
8
∵∠B=90°
∴ AB2+ BF2=AF2
82+ BF2=102
∴BF=6
∴CF=BC-BF=10-6=4
6
4
∵∠C=90°
∴ CE2+CF2=EF2
(8- X)2+42=X2
64 -16X+X2+16=X2
80 -16X=0
16X=80
X=5
3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B ) (C)2 (D)1
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
4、如图,分别以Rt △ABC三边为边向外作三个半圆,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式为 .
1.运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
2.在运用勾股定理时,我们必须首先明确哪两条边是直角边,哪一条是斜边.
3.数学来源与生活,同时又服务于我们的生活.数学就在我们的身边,我们要能够学以致用.
在直角三角形ABC中,∠C=900 ,边BC、AC、AB所对应的边分别为a、b、c则存在下列关系,
勾股定理:
直角三角形中,两条直角边的平方和,等于斜边的平方。
a2+b2=c2
公式变形更常用:
有两种特殊的直角三角形,已知一边可以求另外两边长
a= 5 cm时求b=?c=?
c= 6 cm时求b=?a=?
勾股小常识:勾股数
1、 基本勾股数如:大家一定要熟记
2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,
如:
6、8、10 ; 9、12、15
10、24、26 ; 15、36、39
一个门框尺寸如下图所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
1 m
2 m
∵木板的宽2.2米大于1米,
∴ 横着不能从门框通过;
∵木板的宽2.2米大于2米,
∴竖着也不能从门框通过.
∴ 只能试试斜着能否通过,对角线AC的长最大,因此需要求出AC的长,怎样求呢?
有一个边长为50dm 的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50dm
A
B
C
D
解:∵在Rt△ ABC中,∠B=90°,
AC=BC=50,
∴由勾股定理可知:
如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上的一点,测得CB= 60m,AC= 20m ,你能求出A、B两点间的距离吗? (结果保留整数)
变式:以上题为背景,请同学们再设计其他方案构造直角三角形(或其他几何图形),测量池塘的长AB.
一个2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
D
E
解:在Rt△ABC中,
∵∠ACB=90°
∴ AC2+ BC2=AB2
2.42+ BC2=2.52
∴BC=0.7m
由题意得:DE=AB=2.5m
DC=AC-AD=2.4-0.4=2m
在Rt△DCE中,
∴BE=1.5-0.7=0.8m≠0.4m
答;梯子底端B不是外移0.4m
∵∠DCE=90 °
∴ DC2+ CE2=DE2
22+ BC2=2.52
∴CE=1.5m
如图,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
①求梯子的底端B距墙角O多少米?
②如果梯子的顶端A沿墙角下滑0.5米至C,请同学们:
猜一猜,底端也将滑动0.5米吗?
算一算,底端滑动的距离近似值是多少? (结果保留两位小数)
如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
x
25-x
解:设AE= x km,
根据勾股定理,得
AD2+AE2=DE2
BC2+BE2=CE2
又 ∵ DE=CE
∴ AD2+AE2= BC2+BE2
即:152+x2=102+(25-x)2
答:E站应建在离A站10km处。
∴ X=10
则 BE=(25-x)km
15
10
1、在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
解:设水池的深度AC为X尺,
则芦苇高AD为 (X+1)尺.
根据题意得:BC2+AC2=AB2
∴52+X2 =(X+1)2
25+X2=X2+2X+1
解得:X=12
∴X+1=12+1=13(尺)
答:水池的深度为12尺,芦苇高为13尺.
2、矩形ABCD如图折叠,使点D落在BC边上的点F处,已知AB=8,BC=10,求折痕AE的长。
A
B
C
D
F
E
解:设DE为X,
X
(8- X)
则CE为 (8- X).
由题意可知:EF=DE=X,
X
AF=AD=10
10
10
8
∵∠B=90°
∴ AB2+ BF2=AF2
82+ BF2=102
∴BF=6
∴CF=BC-BF=10-6=4
6
4
∵∠C=90°
∴ CE2+CF2=EF2
(8- X)2+42=X2
64 -16X+X2+16=X2
80 -16X=0
16X=80
X=5
3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是( ).
(A)3 (B ) (C)2 (D)1
分析: 由于蚂蚁是沿正方体的外表面爬行的,
故需把正方体展开成平面图形(如图).
B
4、如图,分别以Rt △ABC三边为边向外作三个半圆,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式为 .
1.运用勾股定理解决实际问题,关键在于“找”到合适的直角三角形.
2.在运用勾股定理时,我们必须首先明确哪两条边是直角边,哪一条是斜边.
3.数学来源与生活,同时又服务于我们的生活.数学就在我们的身边,我们要能够学以致用.
