人教版八年级下册数学5.2.1平行线及其判定(一)教案
文档属性
| 名称 | 人教版八年级下册数学5.2.1平行线及其判定(一)教案 | 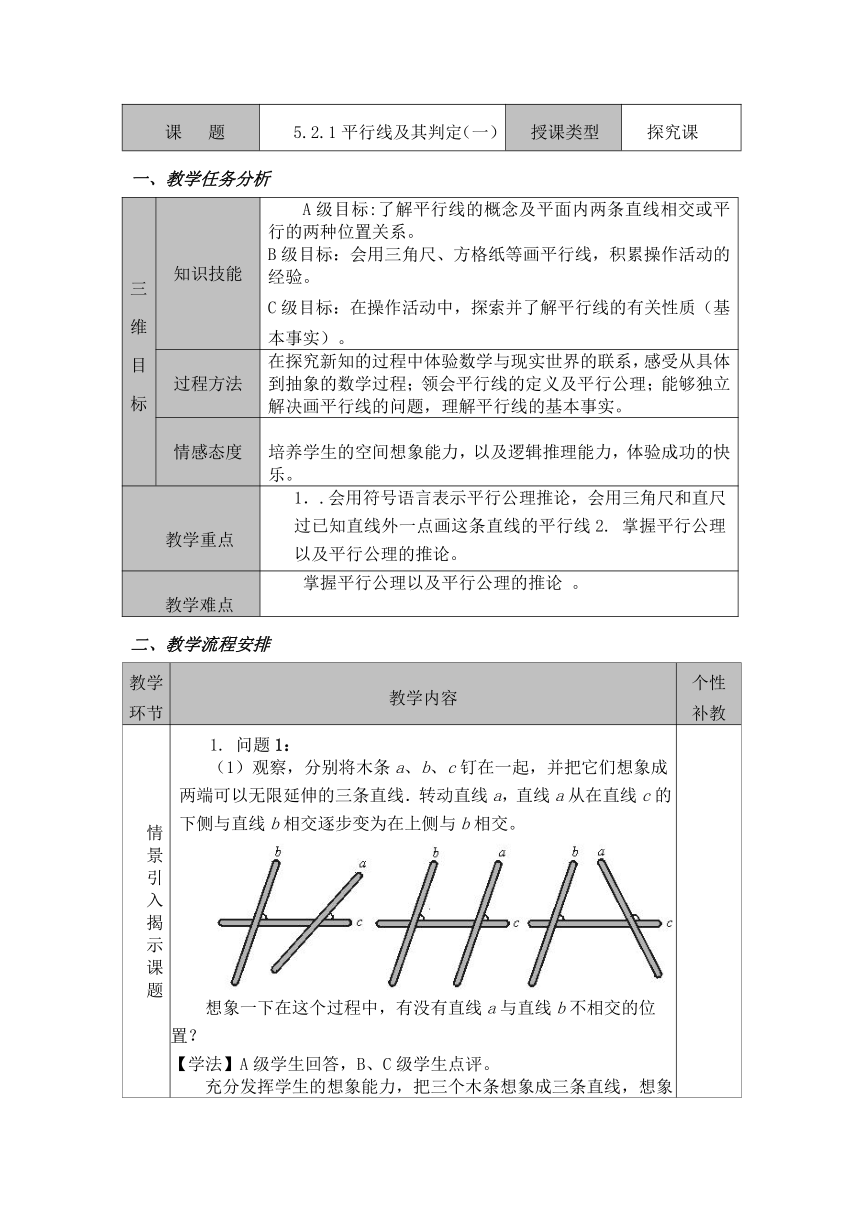 | |
| 格式 | zip | ||
| 文件大小 | 42.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-04-10 10:22:51 | ||
图片预览


文档简介
课 题 5.2.1平行线及其判定(一) 授课类型 探究课
一、教学任务分析
三 维 目 标 知识技能 A级目标:了解平行线的概念及平面内两条直线相交或平行的两种位置关系。 B级目标:会用三角尺、方格纸等画平行线,积累操作活动的经验。 C级目标:在操作活动中,探索并了解平行线的有关性质(基本事实)。
过程方法 在探究新知的过程中体验数学与现实世界的联系,感受从具体到抽象的数学过程;领会平行线的定义及平行公理;能够独立解决画平行线的问题,理解平行线的基本事实。
情感态度 培养学生的空间想象能力,以及逻辑推理能力,体验成功的快乐。
教学重点 1..会用符号语言表示平行公理推论,会用三角尺和直尺过已知直线外一点画这条直线的平行线2. 掌握平行公理以及平行公理的推论。
教学难点 掌握平行公理以及平行公理的推论 。
二、教学流程安排
教学 环节 教学内容 个性 补教
情景 引入 揭示 课题 1. 问题1: (1)观察,分别将木条a、b、c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动直线a,直线a从在直线c的下侧与直线b相交逐步变为在上侧与b相交。 想象一下在这个过程中,有没有直线a与直线b不相交的位置? 【学法】A级学生回答,B、C级学生点评。 充分发挥学生的想象能力,把三个木条想象成三条直线,想象在转动过程中不相交的情况,进而描述两直线平行的定义。 (2)揭示概念:在同一平面内,若直线a和b不相交,那么就称直线a和b平行,记作a//b。 【学法】C级学生回答,A、B级学生聆听。 在学生想象、描述的基础上引导学生进行归纳,教师补充归纳。 学生说出生活中存在的两条直线互相平行的实例。 【学法】A、 B级学生回答, C级学生补充。 滑雪板、正方体中的一些棱、运动跑道,等等。
巩 固 练 习 辨 析 概 念 下列说法中正确的有:________。 (1)在同一平面内不相交的两条线段必平行; (2)在同一平面内不相交的两条直线必平行; (3)在同一平面内不平行的两条线段必相交; (4)在同一平面内不平行的两条直线必相交; (5)在同一平面内,两条直线的位置关系有三种:平行、相交和垂直. 【学法】B级学生分析,C级学生补充,A级学生聆听。 解析:根据平行线的概念进行判断。线段不相交,延长后不一定不相交,(1)错误;同一平面内,直线只有平行和相交两种位置关系,(2)(4)正确,(5)错误;线段是有长度的,不平行也可以不相交,(3)错误.故答案为(2)(4)。 方法总结:同一平面内,两条直线的位置关系只有两种:平行和相交。
例 题 示 范 巩 固 新 知 1.例1: 在活动木条a的过程中,有几个位置使得a与b平行? 【学法】C级学生回答,A、B级学生聆听。 问题(1),可以发现在木条在转动的过程中,只有一个位置使得a与b平行。 如图,经过点B画直线a的平行线,你能有几种方法?可以画几条?经过点C呢? 【学法】A、 B、C级共同作图,A、 B级学生回答,C级学生补充。 可以考虑用小学中学过的画平行线的方法——使用三角板和直尺,如图所示: 经过上述问题的解决,你能得到什么结论? 【学法】C级学生回答,A、B级学生聆听。 对于问题(3),经过画图操作,观察归纳,可以发现一个基本事实(平行公理):经过直线外一点,有且只有一条直线与已知直线平行。 2.例2. 如图,若a//b,b//c,你能得到a//c吗?说明你的理由,从中你能得到什么? 【学法】A、 B级学生回答, C级学生补充。 教师讲解: 假设a与c不平行,则可以设a与c相交于点O,又a//b,b//c,于是过O点有两条直线a和c都与b平行,于是和平行公理矛盾,所以假设不正确,因此a和c一定平行。 教师归纳:平行于同一条直线的两条直线互相平行。 过直线外一点有且只有一条直线与已知直线平行。
巩 固 练 习 辨 析 概 念 有下列四种说法:1.过直线外一点有且只有一条直线与这条直线平行;2.同一平面内,过一点能且只能作一条直线与已知直线垂直;3.直线外一点与直线上各点连接的所有线段中,垂线段最短;4.平行于同一条直线的两条直线互相平行.其中正确的个数是( ) A.1个 B.2个 C.3个 D.4个 【学法】A、 B级学生回答,C级学生补充。(答案为D。)
小结 知识 本节课你有哪些收获? 你还有哪些疑惑? 1. 平行线定义的理解。( A级)。 平行公理以及推论。(B级)。 3.平行公理及推论的应用。(C级)。
三、作业设计:
【A级作业目标】 1. 如图所示,在∠AOB内有一点P. (1)过点P画l1∥OA; (2)过点P画l2∥OB; (3)用量角器量一量l1与l2相交的角与∠O的大小有怎样的关系. 【B级作业目标】 1.同A级1 2. 四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那直线a,d的位置关系为________. 【C级作业目标】 1.同B级2 2. 将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
板书设计: 平行线
四、反思提炼:
一、教学任务分析
三 维 目 标 知识技能 A级目标:了解平行线的概念及平面内两条直线相交或平行的两种位置关系。 B级目标:会用三角尺、方格纸等画平行线,积累操作活动的经验。 C级目标:在操作活动中,探索并了解平行线的有关性质(基本事实)。
过程方法 在探究新知的过程中体验数学与现实世界的联系,感受从具体到抽象的数学过程;领会平行线的定义及平行公理;能够独立解决画平行线的问题,理解平行线的基本事实。
情感态度 培养学生的空间想象能力,以及逻辑推理能力,体验成功的快乐。
教学重点 1..会用符号语言表示平行公理推论,会用三角尺和直尺过已知直线外一点画这条直线的平行线2. 掌握平行公理以及平行公理的推论。
教学难点 掌握平行公理以及平行公理的推论 。
二、教学流程安排
教学 环节 教学内容 个性 补教
情景 引入 揭示 课题 1. 问题1: (1)观察,分别将木条a、b、c钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动直线a,直线a从在直线c的下侧与直线b相交逐步变为在上侧与b相交。 想象一下在这个过程中,有没有直线a与直线b不相交的位置? 【学法】A级学生回答,B、C级学生点评。 充分发挥学生的想象能力,把三个木条想象成三条直线,想象在转动过程中不相交的情况,进而描述两直线平行的定义。 (2)揭示概念:在同一平面内,若直线a和b不相交,那么就称直线a和b平行,记作a//b。 【学法】C级学生回答,A、B级学生聆听。 在学生想象、描述的基础上引导学生进行归纳,教师补充归纳。 学生说出生活中存在的两条直线互相平行的实例。 【学法】A、 B级学生回答, C级学生补充。 滑雪板、正方体中的一些棱、运动跑道,等等。
巩 固 练 习 辨 析 概 念 下列说法中正确的有:________。 (1)在同一平面内不相交的两条线段必平行; (2)在同一平面内不相交的两条直线必平行; (3)在同一平面内不平行的两条线段必相交; (4)在同一平面内不平行的两条直线必相交; (5)在同一平面内,两条直线的位置关系有三种:平行、相交和垂直. 【学法】B级学生分析,C级学生补充,A级学生聆听。 解析:根据平行线的概念进行判断。线段不相交,延长后不一定不相交,(1)错误;同一平面内,直线只有平行和相交两种位置关系,(2)(4)正确,(5)错误;线段是有长度的,不平行也可以不相交,(3)错误.故答案为(2)(4)。 方法总结:同一平面内,两条直线的位置关系只有两种:平行和相交。
例 题 示 范 巩 固 新 知 1.例1: 在活动木条a的过程中,有几个位置使得a与b平行? 【学法】C级学生回答,A、B级学生聆听。 问题(1),可以发现在木条在转动的过程中,只有一个位置使得a与b平行。 如图,经过点B画直线a的平行线,你能有几种方法?可以画几条?经过点C呢? 【学法】A、 B、C级共同作图,A、 B级学生回答,C级学生补充。 可以考虑用小学中学过的画平行线的方法——使用三角板和直尺,如图所示: 经过上述问题的解决,你能得到什么结论? 【学法】C级学生回答,A、B级学生聆听。 对于问题(3),经过画图操作,观察归纳,可以发现一个基本事实(平行公理):经过直线外一点,有且只有一条直线与已知直线平行。 2.例2. 如图,若a//b,b//c,你能得到a//c吗?说明你的理由,从中你能得到什么? 【学法】A、 B级学生回答, C级学生补充。 教师讲解: 假设a与c不平行,则可以设a与c相交于点O,又a//b,b//c,于是过O点有两条直线a和c都与b平行,于是和平行公理矛盾,所以假设不正确,因此a和c一定平行。 教师归纳:平行于同一条直线的两条直线互相平行。 过直线外一点有且只有一条直线与已知直线平行。
巩 固 练 习 辨 析 概 念 有下列四种说法:1.过直线外一点有且只有一条直线与这条直线平行;2.同一平面内,过一点能且只能作一条直线与已知直线垂直;3.直线外一点与直线上各点连接的所有线段中,垂线段最短;4.平行于同一条直线的两条直线互相平行.其中正确的个数是( ) A.1个 B.2个 C.3个 D.4个 【学法】A、 B级学生回答,C级学生补充。(答案为D。)
小结 知识 本节课你有哪些收获? 你还有哪些疑惑? 1. 平行线定义的理解。( A级)。 平行公理以及推论。(B级)。 3.平行公理及推论的应用。(C级)。
三、作业设计:
【A级作业目标】 1. 如图所示,在∠AOB内有一点P. (1)过点P画l1∥OA; (2)过点P画l2∥OB; (3)用量角器量一量l1与l2相交的角与∠O的大小有怎样的关系. 【B级作业目标】 1.同A级1 2. 四条直线a,b,c,d互不重合,如果a∥b,b∥c,c∥d,那直线a,d的位置关系为________. 【C级作业目标】 1.同B级2 2. 将一张长方形的硬纸片ABCD对折后打开,折痕为EF,把长方形ABEF平摊在桌面上,另一面CDFE无论怎样改变位置,总有CD∥AB存在,为什么?
板书设计: 平行线
四、反思提炼:
